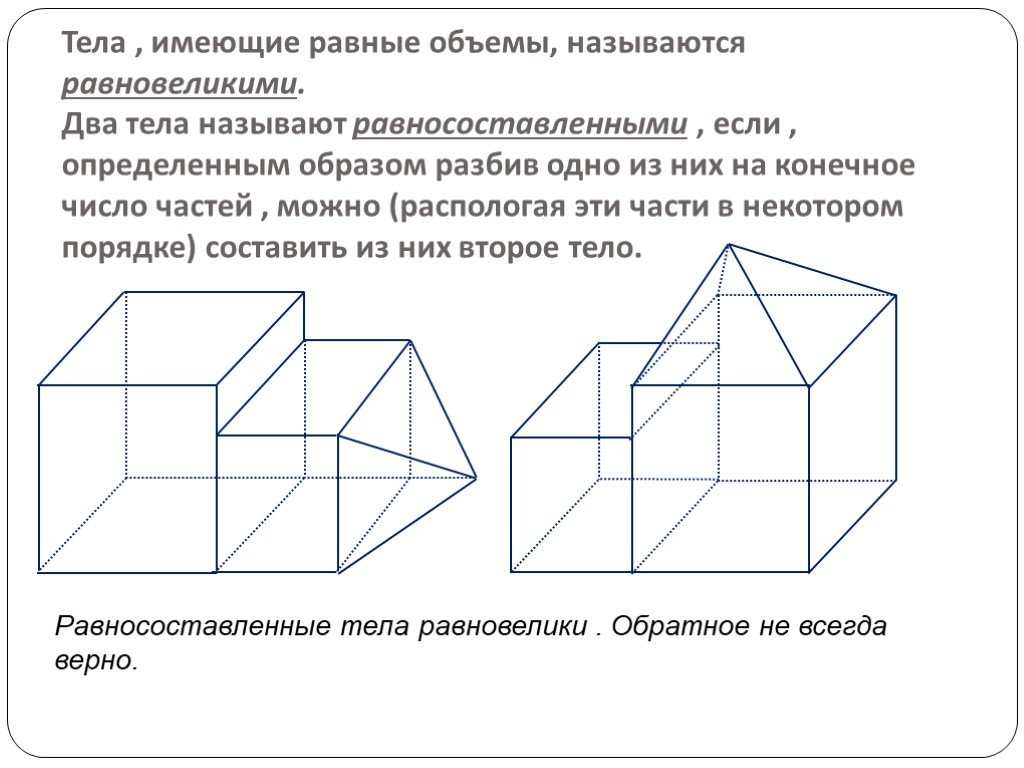
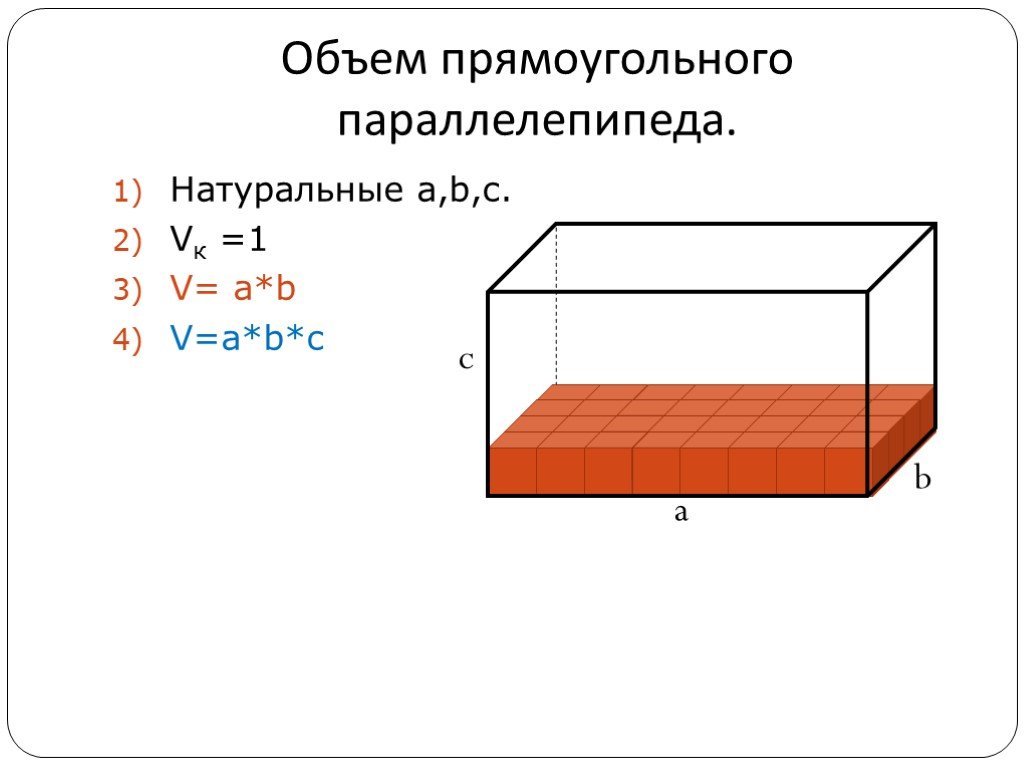
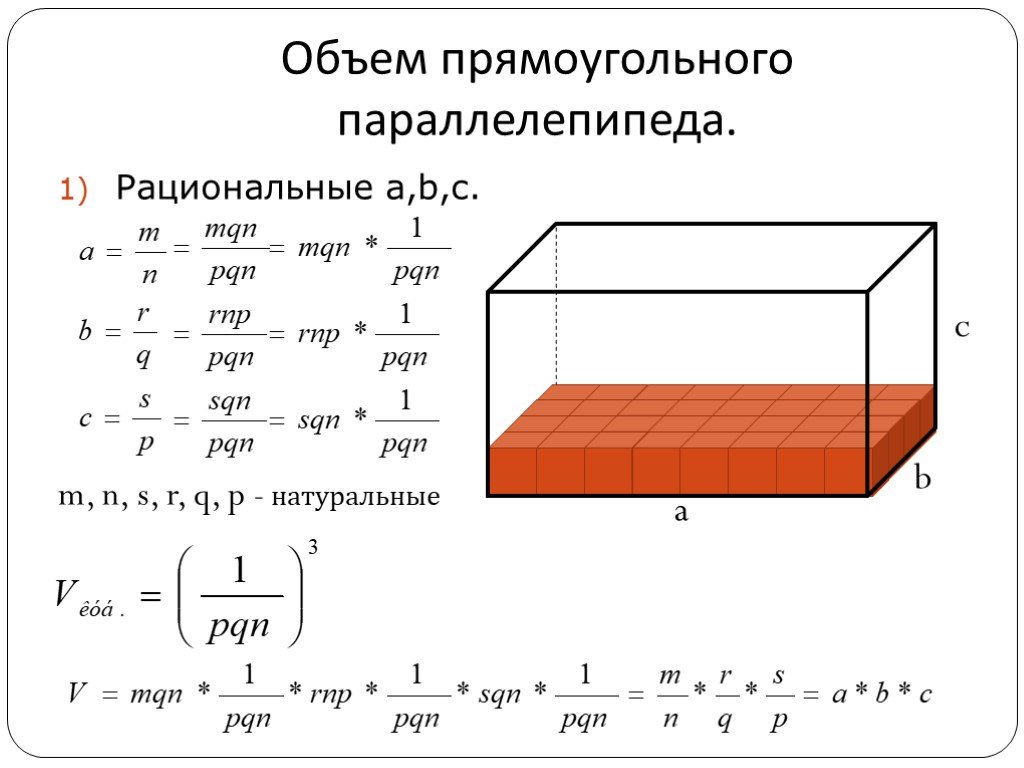
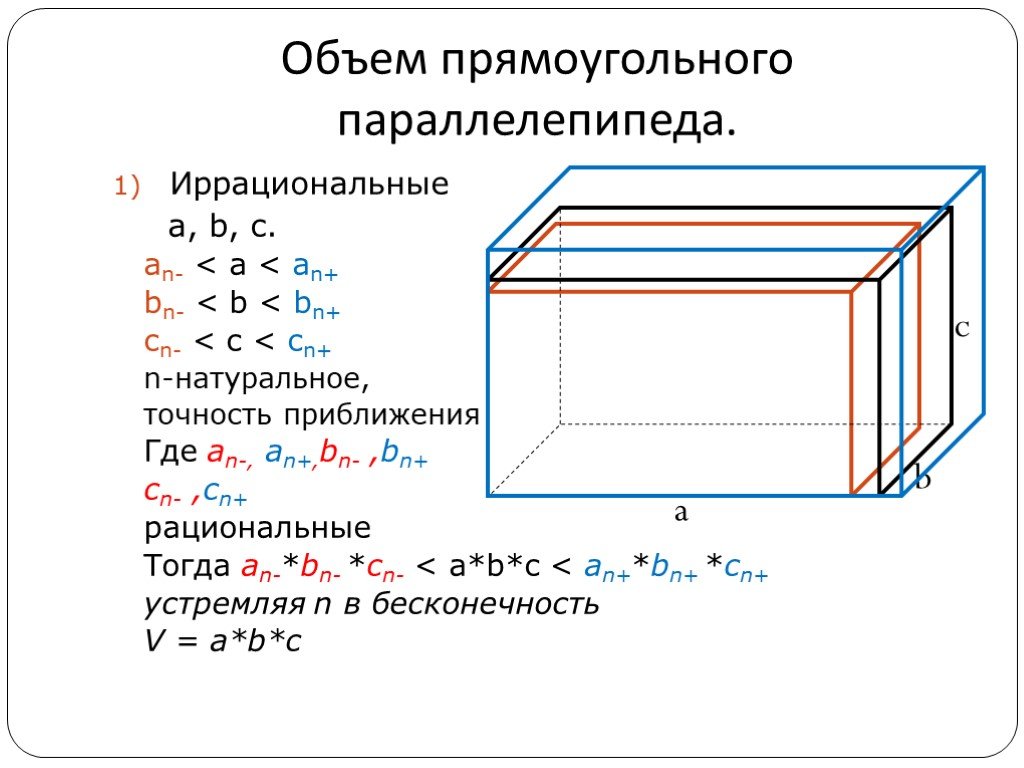
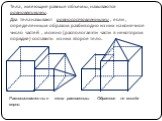
Презентация "Понятие объема многогранников. Объем прямоугольного параллелепипеда" по математике – проект, доклад
Презентацию на тему "Понятие объема многогранников. Объем прямоугольного параллелепипеда" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 12 слайд(ов).
Слайды презентации
Список похожих презентаций
Объем прямоугольного параллелепипеда
ПЛОСКИЕ ОБЪЕМНЫЕ ФИГУРЫ. ПЛОСКИЕ ФИГУРЫ. ТРЕУГОЛЬНИК КВАДРАТ ПРЯМОУГОЛЬНИК КРУГ ЧЕТЫРЕХУГОЛЬНИК. КУБ ЦИЛИНДР ПАРАЛЛЕПИПЕД. ОБЪЕМНЫЕ ФИГУРЫ. Планиметрия ...Объем прямоугольного параллелепипеда
УСТНЫЙ СЧЕТ. второй ТУР: ПУСТЬ ВСЯКИЙ ЗНАЕТ, КТО ЖЕ ЛУЧШЕ ВЫЧИСЛЯЕТ? МНЕ задачи ПРОЧИТАТЬ, ВАМ ЖЕ ДУМАТЬ И СЧИТАТЬ! Возведи в квадрат и куб. 42= 102= ...Объем прямоугольного параллелепипеда
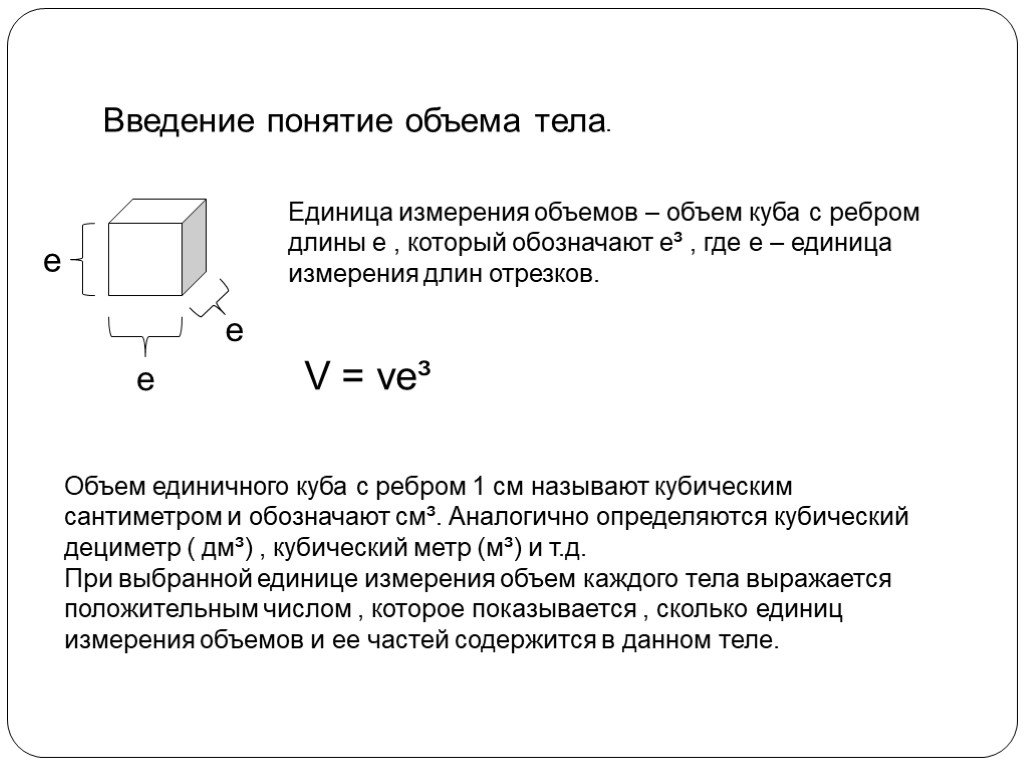
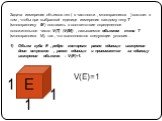
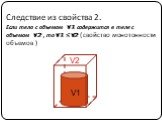
Единицы измерения объемов: 1мм3, 1 см3, 1 дм3, 1 л, 1 м3, 1 км3. Чтобы сравнить объемы двух сосудов, можно наполнить один из них водой и перелить ...Объем прямоугольного параллелепипеда. Решение задач
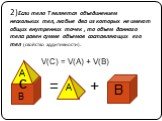
Объем прямоугольного параллелепипеда. Решение задач. ABCDA1B1C1D1–прямоугольный параллелепипед. а) V = a²h б) V = 1/2d²b в) V = abc г) V = 1/2d²bsinφ. ...Объемы. Объем прямоугольного параллелепипеда
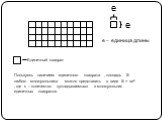
1 = ? 4·16 +11 :15 ·12 -20. 2 19·3 -9 :12 ·25 :10. 3. Соревнование с первоклассником Корова-2,овца-2,свинья-3,собака-3,кукушка-4,лошадь-5,петух-8. ...Единицы измерения длины, площади, объема
Фут- средняя длина ступни человека (английское слово «фут»- ступня). Еще меньшей единицей длины является ДЮЙМ, который был длиной сустава большого ...Вычисление объема тела человека
Архимед (287 - 212 до н.э.). Древнегреческий ученый математик и изобретатель, родился в Сиракузах. Закон Архимеда формулируется так:. Архимедова сила, ...Как находить объём прямоугольного параллелепипеда
"Предмет математики настолько серьезен, что полезно не упускать случая делать его не- много занима- тельным". Блез Паскаль. Геометрические тела и ...Решение задач.Применение интеграла к вычислению площади и объема геометрических фигур
Найти одну из первообразных. ; ; ; . Вычислить интеграл. 1. ; 3. ; 2. ; 4. . ...Сечения прямоугольного параллелепипеда и тетраэдра
№82. Отметьте внутр.точку М грани АА1В1В. Постр. сеч. прох. ч/з т.М и параллельно а)(АВСD); б)(ВВ1С1С); в)(BDD1). А В С D B1 C1 D1 А1. М1 М. №82 в. ...Свойства прямоугольного параллелепипеда
Цели:. Определение прямоугольного параллелепипеда Измерения прямоугольного параллелепипеда Формулы для нахождения его квадрата диагонали Формула для ...Применение формул объёма и площади поверхности прямоугольного параллелепипеда
Цель урока: Научиться на практике применять формулы объёма и площади поверхности прямоугольного параллелепипеда. Устный опрос. Сколько ребер у параллелепипеда? ...Объём прямоугольного параллелепипеда
Блиц-Опрос. Прямоугольный параллелепипед – это (плоская, объёмная) фигура. Стороны граней параллелепипеда называются _______________. У параллелепипеда ...Объемы параллелепипеда и призмы
Цель:. учиться применять формулы объема параллелепипеда и призмы при решении различных задач. План урока. Повторение пройденного материала. Физический ...Объем параллелепипеда
Объем куба. Объем куба с ребром а вычисляется по формуле. а. Объем прямоугольного параллелепипеда вычисляется по формуле. Объем любого параллелепипеда ...Объём прямоугольного параллелепипеда
. «Дорогой Хагрид! Оставляю под Вашим присмотром этого дракончика, для которого срочно придётся приобрести аквариум, так как на суше его можно держать ...Понятие пирамиды
Маршрут путешествия. Египет- страна Пирамид Пирамиды на Марсе Пирамиды в химии Пирамиды в экономике Пирамиды в геометрии. Путешествие вокруг света. ...Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Понятие многогранника
Многогранники Тела. Геометрические фигуры. Плоские Не многогранники. Определение многогранника. Многогранником называется ограниченное тело, поверхность ...Типы параллелепипеда
Параллелепипед - призма, основанием которой служит параллелограмм. Типы параллелепипеда. Различается несколько типов параллелепипеда: Прямоугольный ...Конспекты
Формула объема прямоугольного параллелепипеда
ОТКРЫТЫЕ УРОКИ. Учитель: Забродина Н.Д. 3 класс. Урок математики. Тема:. Формула объема прямоугольного параллелепипеда. Цели:. Углубить ...Объем прямоугольного параллелепипеда
Осмоловская Нина Федоровна. учитель математики. Муниципального общеобразовательного учреждения Усвятская средняя общеобразовательная школа Дорогобужского ...Объемы. Объем прямоугольного параллелепипеда
Урок математики в 5 классе. . . Тема:. Объемы. Объем прямоугольного параллелепипеда. Цель:. 1. Закрепить знания по данной теме при решении задач. ...Прямоугольный параллелепипед. Объем прямоугольного параллелепипеда
Технологическая карта урока. Разработчик. : учитель математики ГБОУ СОШ с. Криволучье-Ивановка. Самарской обл., Красноармейского р-она Баранов ...Объем прямоугольного параллелепипеда
Предмет — математика. . Класс: 5. Тема урока:. Объем прямоугольного параллелепипеда. Главная дидактическая цель:. закрепление навыков. ...Куб, как частный случай прямоугольного параллелепипеда
Конспект урока математики. 9 класс. Тема: «Куб, как частный случай прямоугольного параллелепипеда». Автор: Старикова Галина Владимировна, учитель ...Площадь поверхности прямоугольного параллелепипеда
Тема урока. . Площадь поверхности прямоугольного параллелепипеда. . . Базовый учебник. . Математика, 5 класс, Виленкин. . . . Цель ...Решение задач на вычисление объема цилиндрических и конических тел
Урок 5. Тема урока:. Решение задач на вычисление объема цилиндрических и конических тел. Тип учебного занятия:. Обобщение и систематизация знаний ...Объем наклонного параллелепипеда. Объем призмы
Технологическая карта. Класс – 11. Предмет – геометрия. Тема - Объем наклонного параллелепипеда. Объем призмы. Проверка домашнего задания. ...Объём куба и прямоугольного параллелепипеда. Кубический см
Ленинская средняя школа. Разработка открытого урока математики в 4 классе на тему:. « Объём куба и прямоугольного ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:3 апреля 2019
Категория:Математика
Содержит:12 слайд(ов)
Поделись с друзьями:
Скачать презентацию