Презентация "Тригонометрические неравенства" по математике – проект, доклад
Презентацию на тему "Тригонометрические неравенства" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).
Слайды презентации
Список похожих презентаций
Тригонометрические неравенства
Цели урока. Сформировать умения решать тригонометрические неравенства Закрепить решение простейших тригонометрических уравнений Развивать инициативность, ...Тригонометрические функции
Содержание. Введение................................................... .......3-5слайд Начало изучения..............................................6-7 ...Тригонометрические формулы
Цель урока. Повторить и систематизировать изученный материал Подготовиться к контрольной работе. Задачи урока. Повторить определение синуса, косинуса, ...Тригонометрические уравнения. Методы решений
История тригонометрии. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon - треугольник, а metrew- ...Тригонометрические уравнения и методы их решения
«Великая книга природы открыта для нас, но научиться понимать ее можно лишь путем прилежания, любви, страданий. Язык этот-математика. Математика расцветает ...Линейные неравенства с параметром
Ах = В А = 0 0х = В В = 0 0х = 0 Х = R Корней нет х =В : А 1 корень. Алгоритм решения линейных уравнений с параметром. 1.Найти ДЗП ( допустимые значения ...Числовые неравенства
Самостоятельная работа. Вариант 1 Дайте определение, что число a больше числа b Сравните: а) б) а2 + 16 и 8а Докажите неравенство (а – 3)(а + 9 ). ...Тригонометрические функции углов в произвольном треугольнике 1-2
Продолжите фразу:. Синусом острого угла прямоугольного треугольника называется. А С В. отношение противолежащего катета к гипотенузе. Косинусом острого ...Показательные уравнения и неравенства
Цель урока: обобщение знаний о способах решения показательных уравнений и неравенств, подготовка к ЕГЭ. 2. 1. если , то если , то решений нет. Показательные ...Показательные уравнения и неравенства
"Что значит решить задачу? Это значит свести ее к уже решенным". С.А. Яновская. - Какие из данных уравнений являются показательными? 12). Определение. ...Показательные и логарифмические неравенства
Лекция №5. Показательные и логарифмические неравенства. 1. Показательные неравенства 1.1. Решение простейших показательных неравенств. Простейшими ...Логарифмические уравнения и неравенства
Цель урока. Повторение свойств логарифмов и логарифмической функции. Отработка навыков при решении логарифмических уравнений и неравенств. Определение ...Логарифмические неравенства
При изучении логарифмических функций рассматриваются неравенства вида: logax < b logax ≥ b. logax > logay x>0; y>0 eсли а>0, то x>y eсли 0. Пример ...Логарифмические неравенства
Секреты знаков произведения (a-1)(b- 1) и выражения logab. Творческое название:. Основополагающий вопрос:. Какова степень эффективности указанного ...Тригонометрические функции
Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника 1) Синус - отношение противолежащего катета ...Тригонометрические функции одного и того же аргумента
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной ...Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа.
1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ. 2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ. 3. У = - f (- x) ← y = f(x), симметрия ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Равенства и неравенства
И так, друзья, внимание. Ведь прозвенел звонок. Садитесь поудобнее -Начнем скорей урок! Работаем в паре 7 * 9 = 63 в > 4 а + 6 > 45 * 2 а + 8 = 27 ...Числовые неравенства и их свойства
Для любых неравных действительных чисел a и b можно сказать, какое больше, а какое меньше. a>b => a – b>0; если a – b. Знаки неравенств. Строгие неравенства: ...Конспекты
Тригонометрические преобразования, уравнения и неравенства
Огаркова И.И. МБОУ «Северомуйская СОШ». Тема урока:. . «Тригонометрические преобразования, уравнения и неравенства». Класс. : 10. Тип урока. ...Тригонометрические уравнения
Урок соревнование. Тема. «Тригонометрические уравнения». Девиз урока. :. «. Один за всех и все за одного». Ход урока:. Урок –соревнование будет ...Тригонометрические уравнения
Конспект урока алгебры и начала анализа в 11 классе. по теме: «Тригонометрические уравнения (урок обобщения и систематизации знаний)». учителя ...Тригонометрические уравнения
Урок-игра по алгебре и началам анализа в10 классе. . Тема «Тригонометрические уравнения». Девиз урока: . “Один за всех и все за одного”. Цель:. ...Тригонометрические преобразования
Технологическая карта урока математики. . по теме «Тригонометрические преобразования». Дата проведения. 18.02.2013г. Учитель:. Волынкина Э. ...Числовые равенства и неравенства
Урок математики. Дата 16.01. Тема. :. «Числовые равенства и неравенства». Цель. : продолжить формировать. знания о числовых равенствах и неравенствах. ...Уравнение и неравенства с модулем
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №30 им. Н.Н. Колокольцова». Кемеровской области Калтанского ...Тригонометрические формулы
Алгебра 10 класс. Разработал:учитель математики первой категории. МАОУ УЛу-Юльской СОШ. Олей В.И. Тема урока:Тригонометрические формулы. Вид ...Логарифмические уравнения и неравенства
Тема. : «Логарифмические уравнения и неравенства». Цели: Проверить теоретические и практические знания по теме; отработать навыки решения логарифмических ...Логарифмические неравенства
МБОУ Старогородковская СОШ. План конспект урока по теме:. Логарифмические неравенства. Ерашкова Наталья Александровна, учитель математики ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:1 мая 2019
Категория:Математика
Содержит:13 слайд(ов)
Поделись с друзьями:
Скачать презентацию




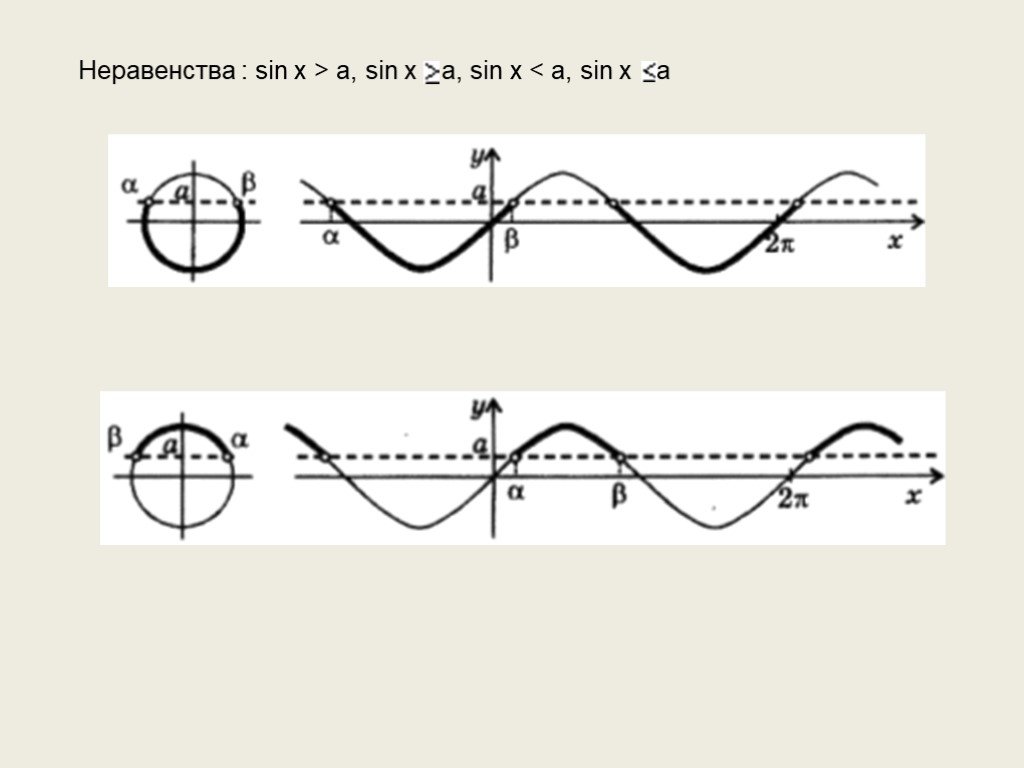



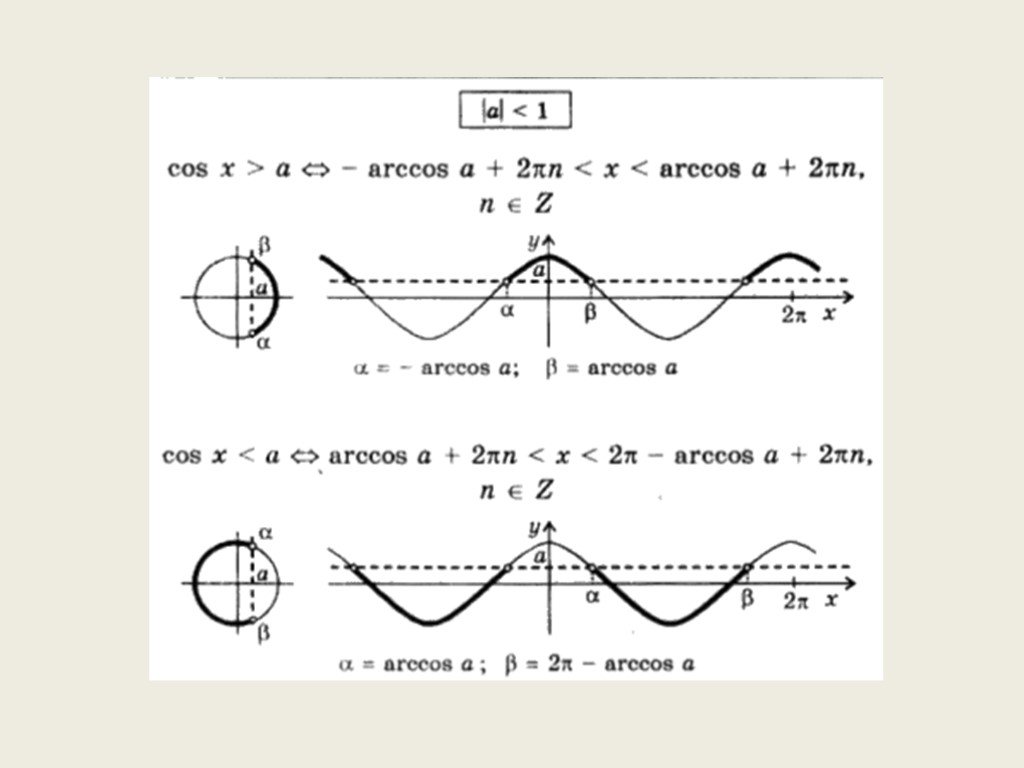


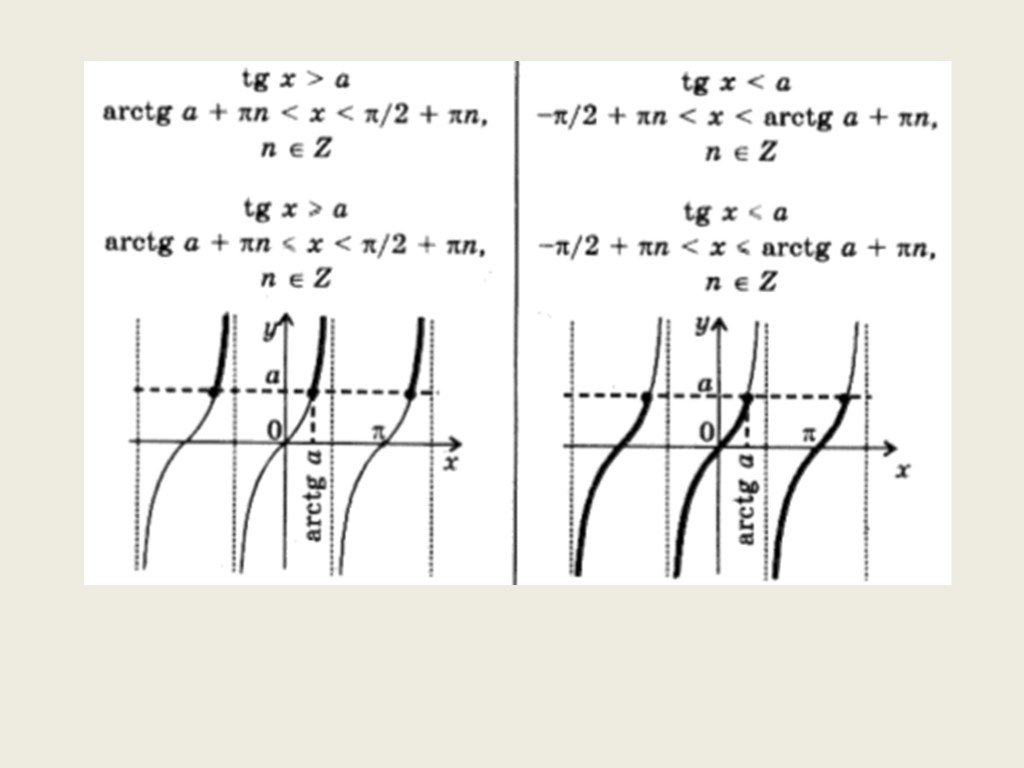





![Пример 1. Решите неравенство Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x [0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n то sin x также Пример 1. Решите неравенство Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x [0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n то sin x также](https://prezentacii.org/upload/cloud/19/05/140855/images/thumbs/screen7.jpg)

































