Конспект урока «Уравнения и неравенства с модулем» по алгебре для 8 класса
Приложение №5
Профильная практика
Урок для 8 класса «Уравнения и неравенства с модулем»
-
Вспомним определение модуля числа
Решить простейшие уравнения с модулем с помощью определения:
-
| x | = 2
-
| x-2 | = 0
-
| 3x-5 | = -2
-
| 3 – 4x | = 3
-
Геометрический смысл модуля
| a | – расстояние от точки А (а) координатной прямой до начала отсчета.
1) | x | = 3 2) | x | ≥ 3 3) | x | ≤ 3


 X
X 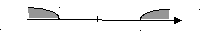 X
X  X
X
-3 0 3 -3 0 3 -3 0 3
Ответ: -3;3 ![]()
Ответ: ![]() Ответ: [ - 3; 3]
Ответ: [ - 3; 3]
Решить неравенства, используя геометрический смысл модуля:
4) | 1+x | ≤ 0,3 5) | 3-2x | > ![]()
6) | x-2 | ≤ a 7) | 3 – 2x | ≥ a
-
Решение уравнений с модулем
Решить уравнение несколькими способами: | x – 1 | = | x – 2 |
1 способ: 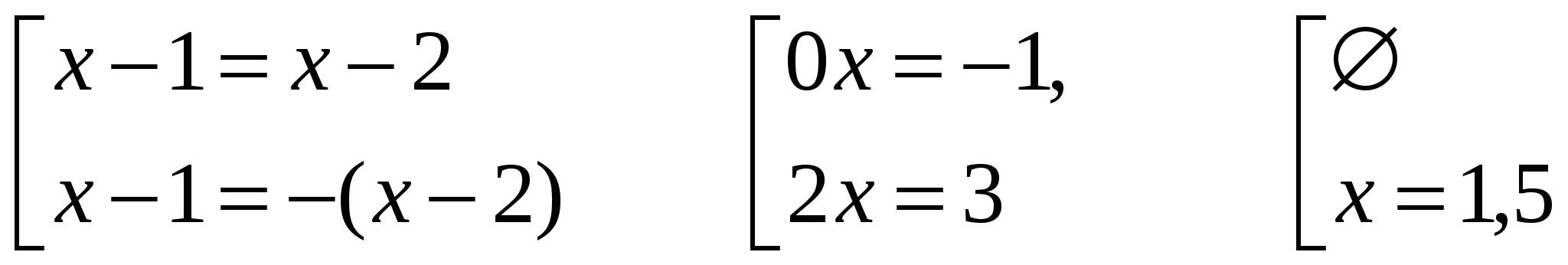
2 способ: подмодульные корни x = 1 , x = 2
– + + x-1
 – 1 – 2 + x-2
– 1 – 2 + x-2
a) x x x ≥ 2
1 – x = 2 – x x – 1 = 2 – x x – 1 = x – 2
0x = 1 2x = 3 0x = –1
![]() x = 1,5
x = 1,5 ![]()
Решить самостоятельно а) | x + 3 | = | x – 5 |
б) | x + 6 | + 4x =5
в) ![]()
-
Где еще мы встречались с модулем?
![]()
– тождество
Решить уравнение ![]()
так как ![]() , то
, то
| x – 7 | = x – 7 , значит
x – 7 ≥ 0 по определению модуля
x ≥ 7
Ответ: [ 7 ; ∞ )
Упростить выражение
1) ![]()
2 )
) ![]() y
y
Построить график функции
![]()
![]()
![]() 0 1 x
0 1 x
Построить график функции
-
y = | x2 – 5x + 6|
б) y = x2 – 5| x | – 6
в) y = ![]()
-
Решить неравенство с модулем
-
| x | > 6 – 2x




![]()







 x x
x x
0 2 0 6
Ответ: ( 2 ; ∞)
-
2
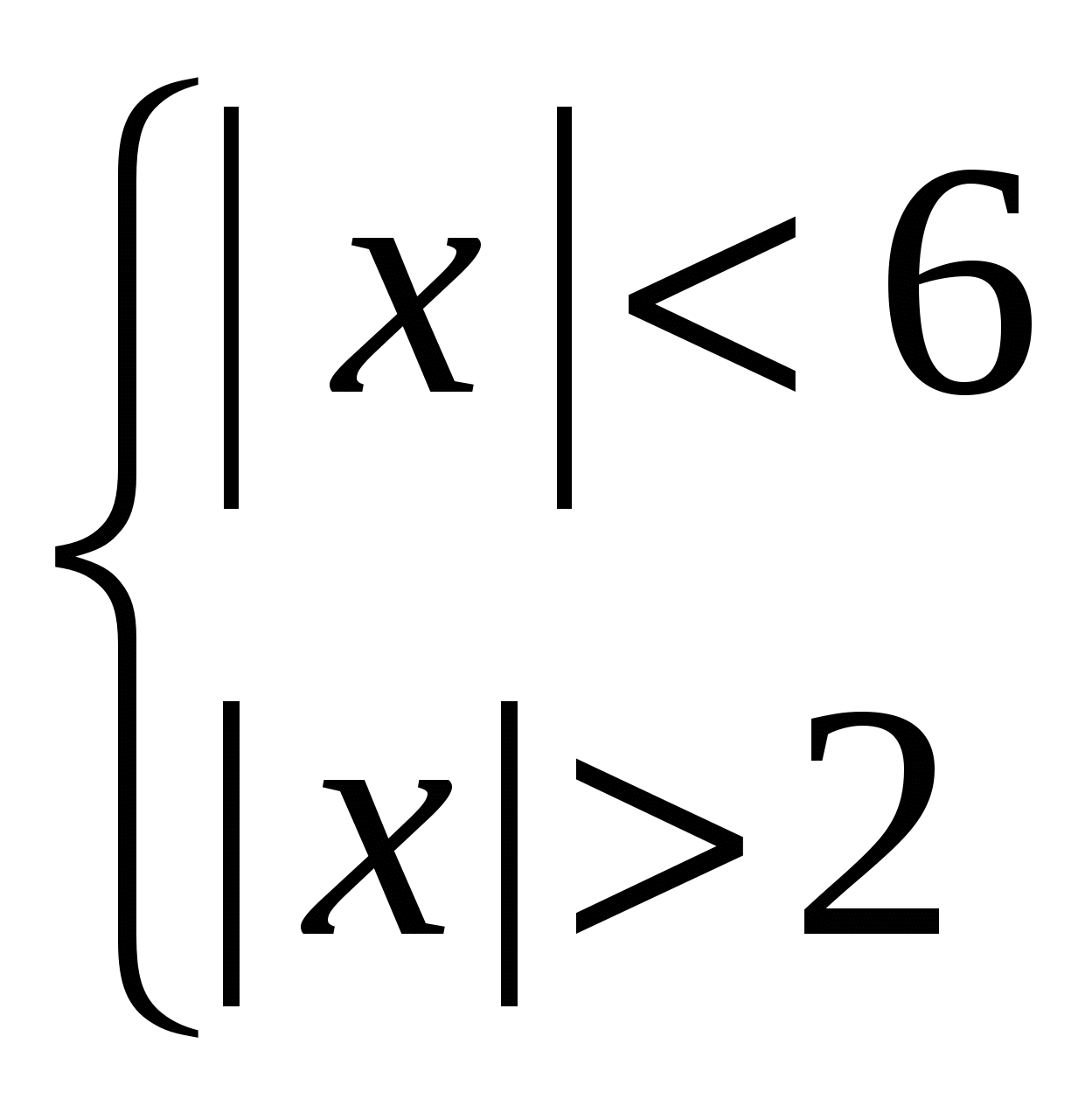
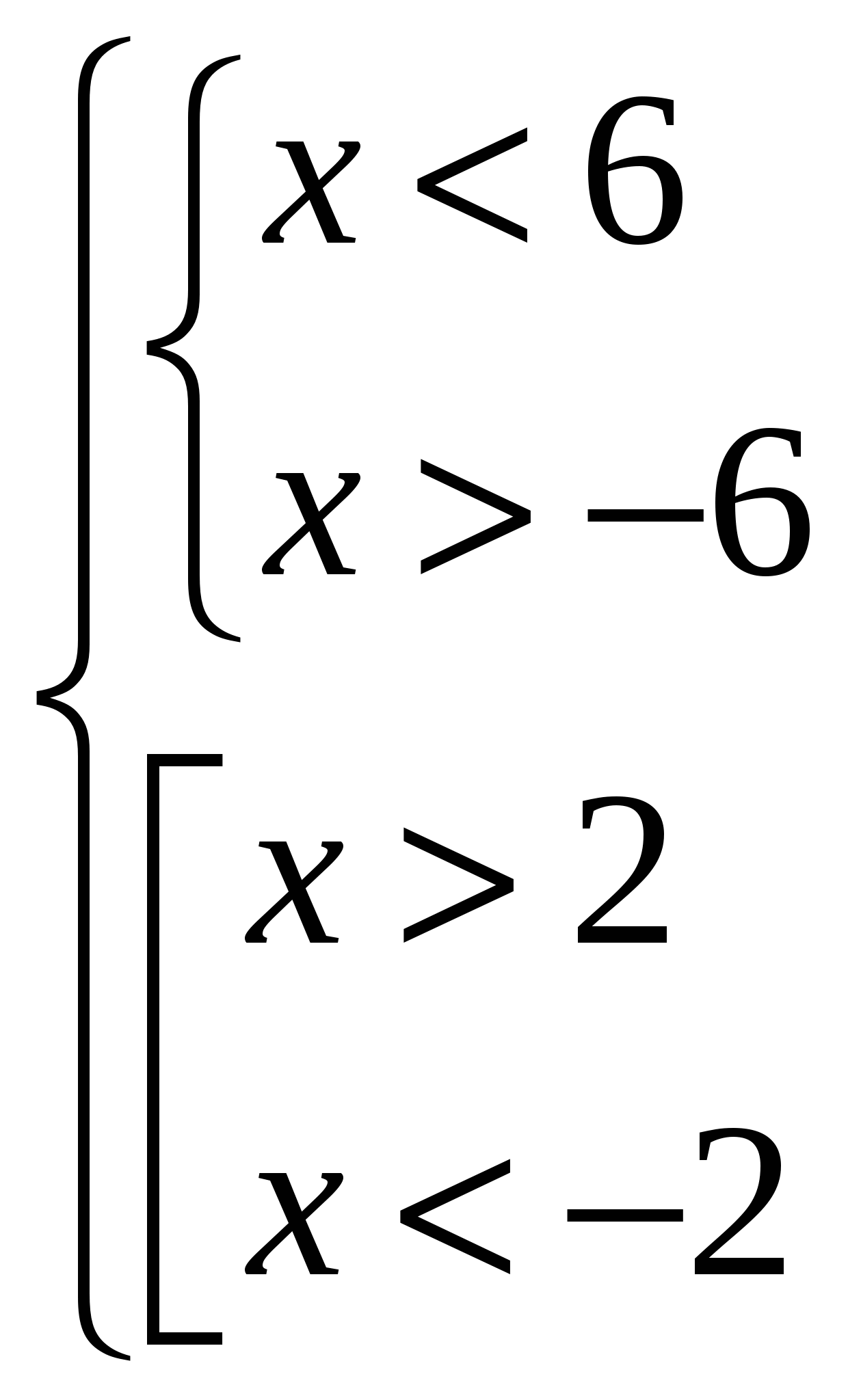
О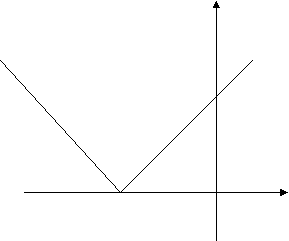 твет: (– 6 ; – 2) U (2 ; 6) y
твет: (– 6 ; – 2) U (2 ; 6) y
-
| x2 + 4x + 3 | > | x + 3 |
решим графическим способом
y = | x2 + 4x +3 |
x2 + 4x +3 = 0
x1 = –1, x2 = –3 – нули функции
![]() , yв = –1
, yв = –1
y = | x + 3 |
x
Ответ: (–∞ ; –3 ) U ( –3 ; –2 ) U ( 0 ; ∞ ) –3 –2 –1 0
Решить неравенства самостоятельно:
-
| 2x + 3 | > | 4x – 3 |
-
| x2 – x + 1 | ≤ | x2 – 3x + 4 |
Обобщающая лекция по теме
«Уравнения и неравенства с параметром»
8 класс
-
Для каждого значения а решите уравнение
(5a – 1)x = 2a + 3
если ![]()
0x = 3,4
![]()
если ![]()
-
Для каждого b решите уравнение
(b2 – 9)x = b + 3
b2 – 9 = 0
b = ± 3
если b = 3, то 0x = 6, ![]()
если b = -3, то 0x = 0, x R
если b ≠ ± 3, то ![]()
-
При каком значении а уравнение не имеет решений?
(3x – a)2 +(4x + 1)2 = (5x – 1)2
9x2 – 6ax + a2 + 16x2 +8x + 1 = 25x2 – 10x + 1
10x – 6ax + 8x = – a2
6(3 – a)x = – a2
если а = 3, 0х = – 9, ![]()
если а ≠ 3, ![]()
Ответ: при а = 3 уравнение не имеет решений.
-
Для каких значений b уравнение x2 – bx + 2b – 3 = 0 имеет один корень?
D = 0, D = b2 – 4(2b – 3) = b2 – 8b + 12
b2 – 8b + 12 = 0
D = 64 – 48 = 16
b1 = 6, b2 = 2
Ответ: при b = 6 и b = 2 уравнение имеет один корень
-
При каких а уравнение имеет два различных корня?
x2(a – 2) + ax + 1 = 0
квадратное уравнение имеет два различных корня, если D > 0
D = a2 – 4(a – 2) = a2 – 4a + 8
a2 – 4a + 8 >0 Если а = 2, то уравнение будет линейным
y = a2 – 4a + 8 0 + 2x + 1 = 0
D = 16 – 32 корень

Ответ: при а ≠ 2 уравнение имеет два
различных корня
 a
a
x R
Решите самостоятельно
-
Для каждого значения m решите уравнение
![]()
Ответ: при m = 4 один корень x = –1 ,
при m = -1 один корень x = 4,
при m ≠ 4, m ≠ –1 два корня x = 4, x = – 1
-
Для каждого значения а найдите число различных корней уравнения
(3x – 1)(ax2 + 3x – 2) = 0
Ответ: при ![]() один корень
один корень
при ![]() , а = 0, а = 9 два различных корня
, а = 0, а = 9 два различных корня
при ![]() три различных корня
три различных корня
Здесь представлен конспект к уроку на тему «Уравнения и неравенства с модулем», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

