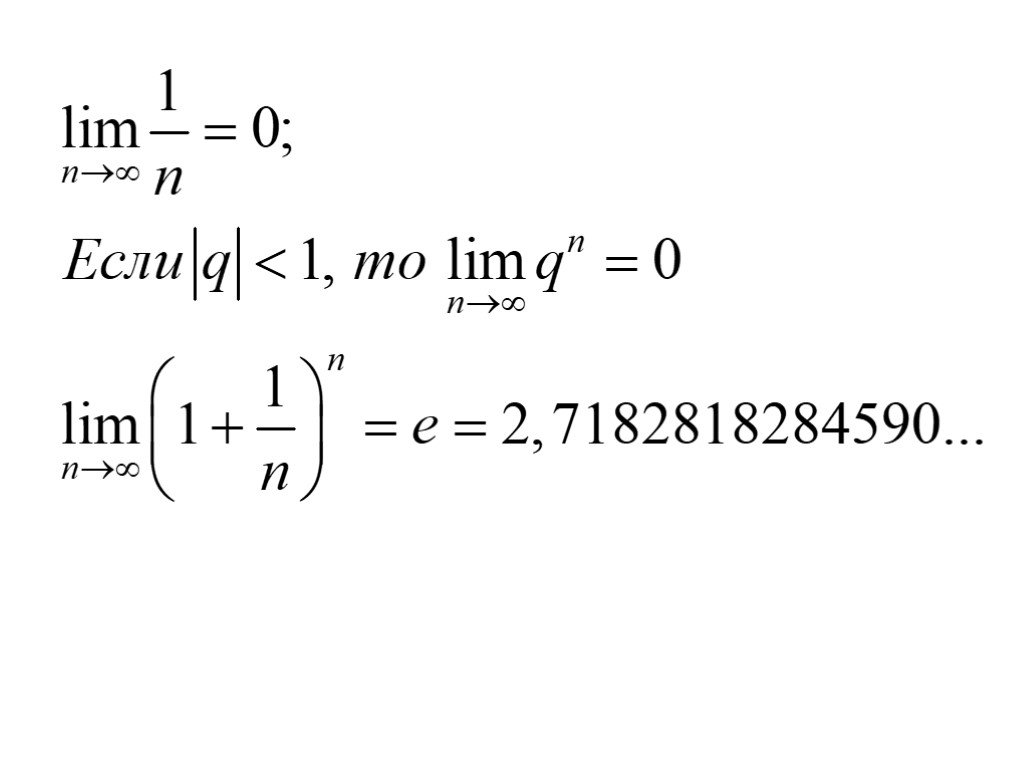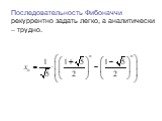Презентация "Предел числовой последовательности" по математике – проект, доклад
Презентацию на тему "Предел числовой последовательности" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 54 слайд(ов).
Слайды презентации
Список похожих презентаций
Предел числовой последовательности
Содержание. Понятие числовой последовательности Примеры числовых последовательностей Способы задания последовательностей Ограниченность числовых последовательностей ...Предел последовательности чисел
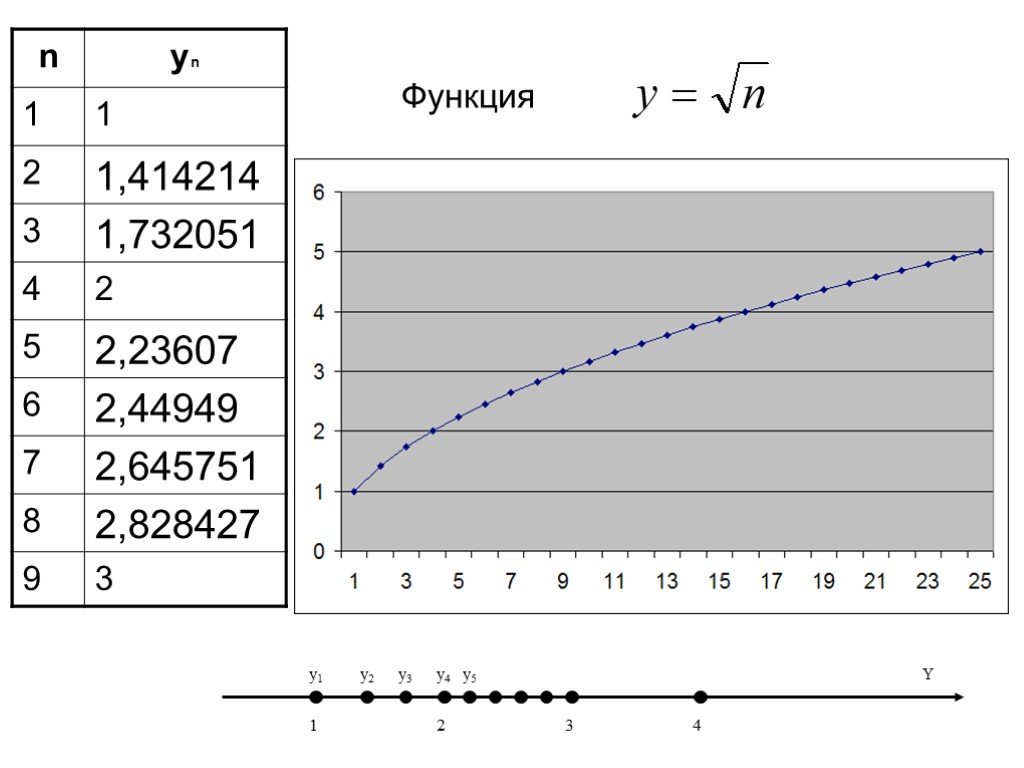
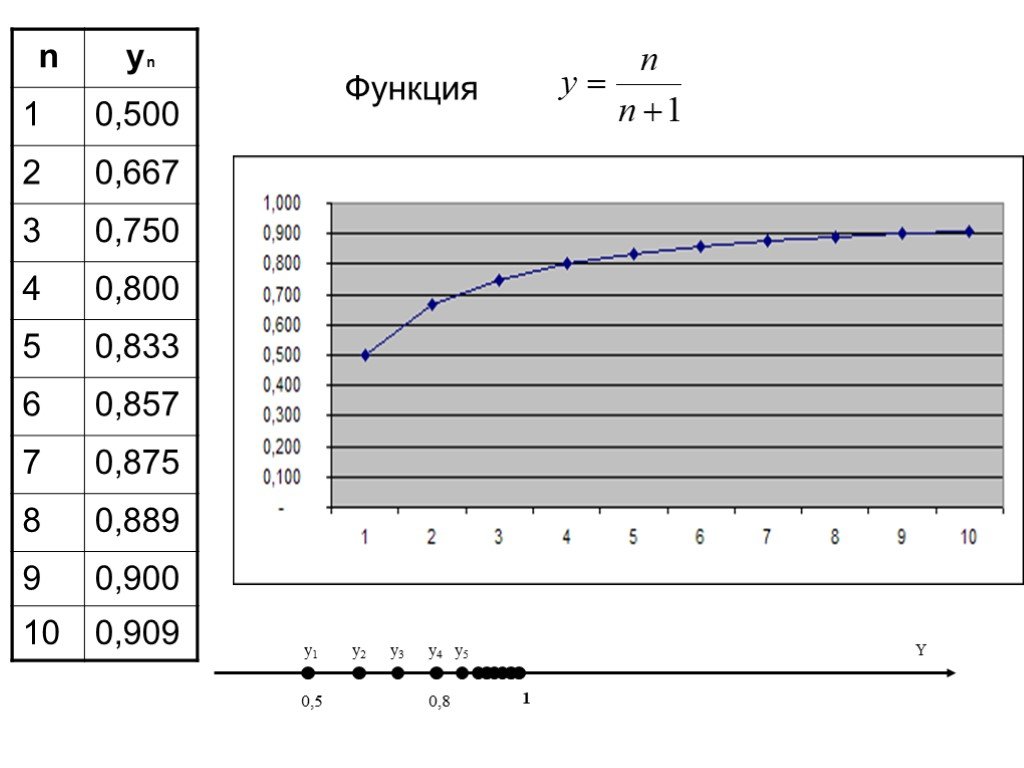
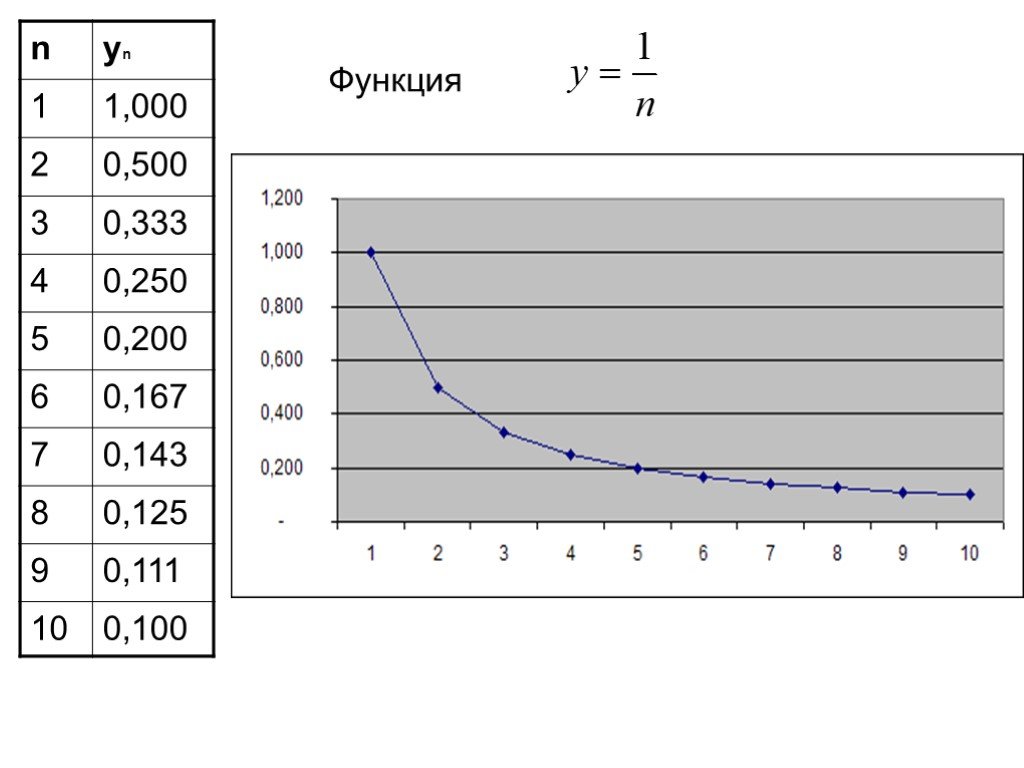
Определение 1. Функцию вида у= f (х), х ϵ Ν называют функцией натурального аргумента или числовой последовательностью и обозначают у = f (n) или у1, ...Числовые последовательности
Ты можешь стать умнее тремя путями: путем опыта – это самый горький путь; путем подражания – это самый легкий путь; путем размышления – это самый ...Числовые последовательности
Числовые последовательности. Функцию вида y=f(x), где xєΝ, называют функцией натурального аргумента или числовой последовательностью и обозначают ...Числовая окружность. Запись чисел числовой окружности
+ – 0;2П; 4П. - 2П; -4П. П -11П 6 6 П -7П 4 4 П -5П 3 3 2П -4П 3 3 3П -4П 4 3 5П -7П 6 6 7П -5П 6 6 5П -3П 4 4 4П -2П 3 3 5П -П 3 3 7П -П 4 4 11П ...Точки на числовой окружности
. оглавление. Числовая окружность на координатной плоскости Дидактические игры Тригонометр. Литература. Центр числовой окружности совместим. с центром ...Представление числовой информации с помощью систем счисления
Система счисления. - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых ...Предел функции в точке
Рассмотрим функции, графики которых изображены на следующих рисунках:. Во всех трех случаях изображена одна и та же кривая, но все же изображают они ...Предел функции в точке
Одна и та же кривая, три разные функции. Отличие – поведение в точке х = а. f(a) – не существует, т.к. в точке х =а функция у = f(х) не определена. ...Предел функции в бесконечности и в точке
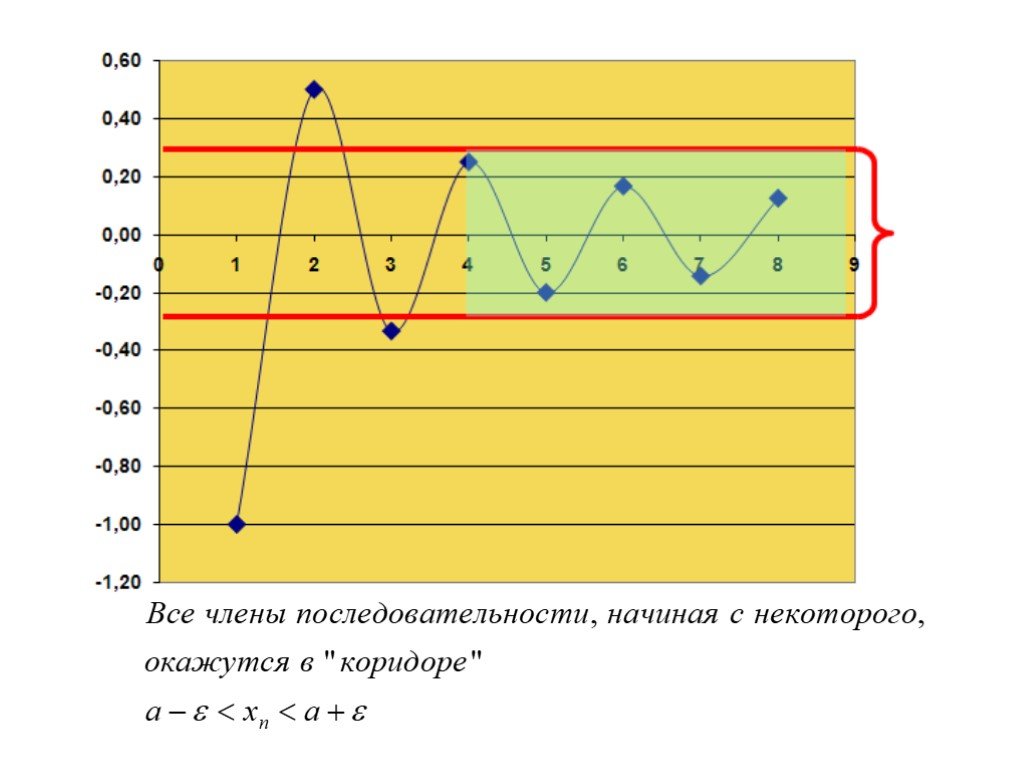
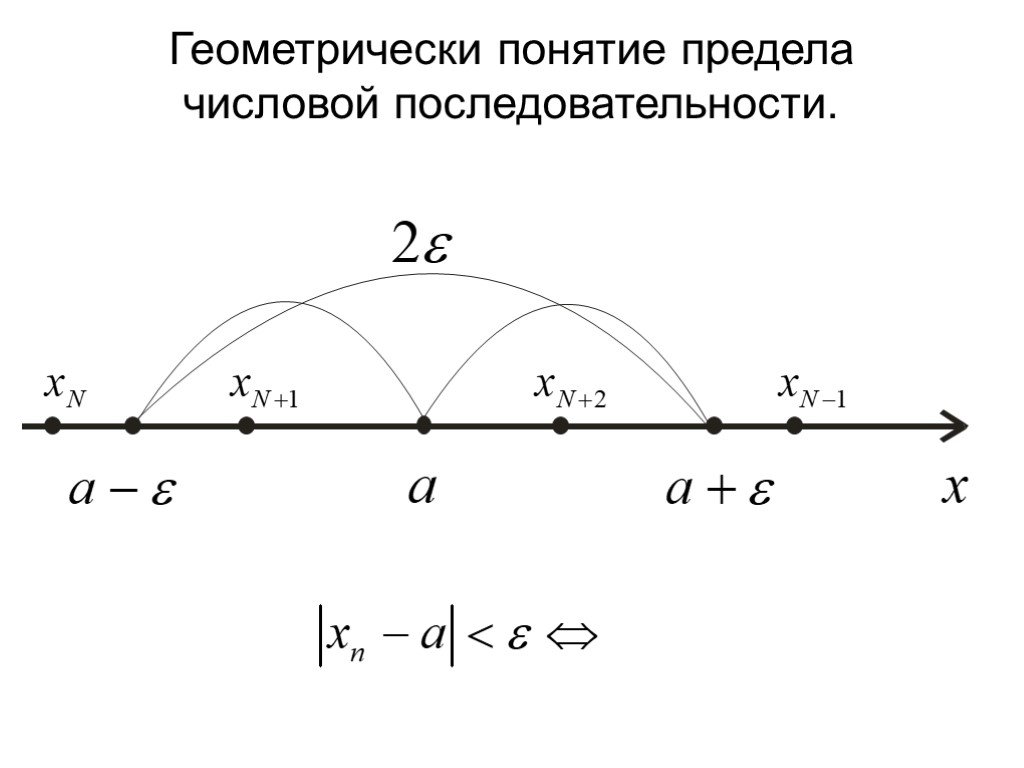
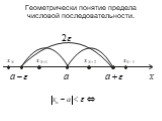
Число А называется пределом функции у=f(x), при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε>0, найдется такое положительное ...Предел функции
Содержание. Предел функции в точке Односторонние пределы Предел функции при x стремящемся к бесконечности Основные теоремы о пределах Вычисление пределов ...Предел переменной величины
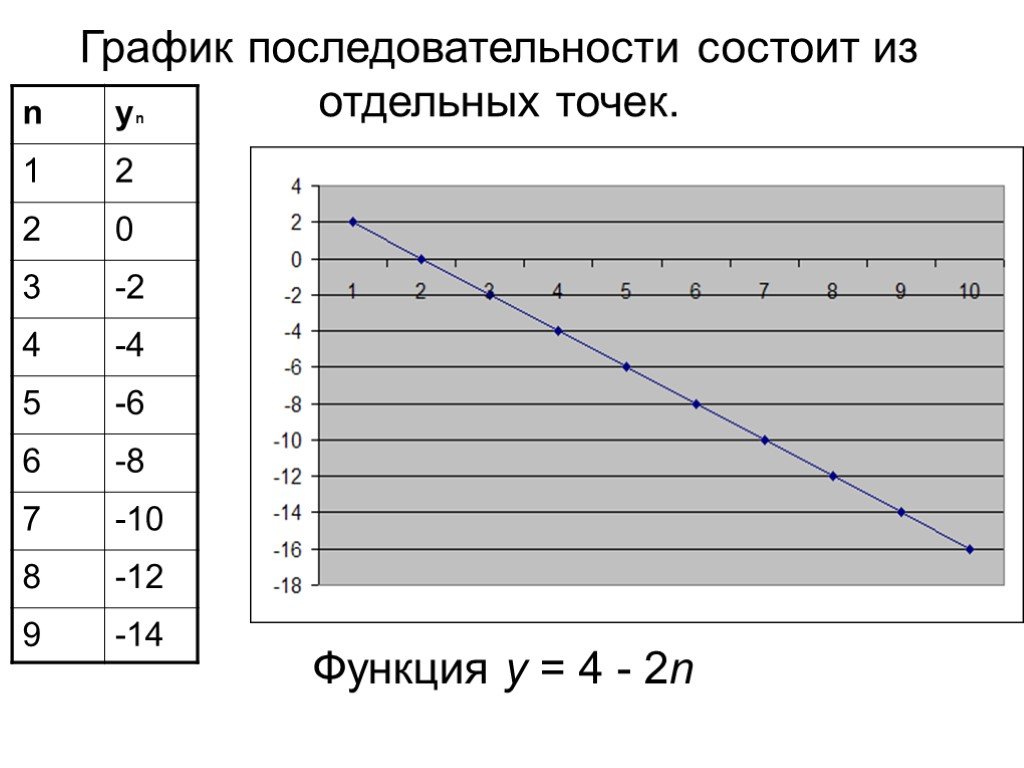
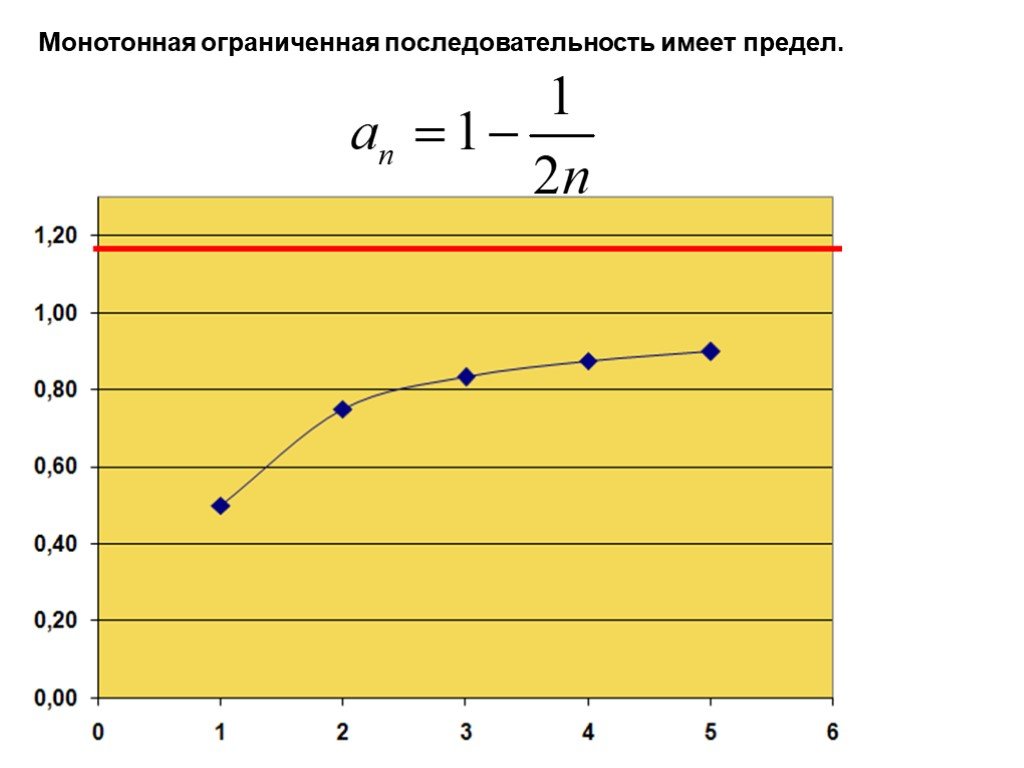
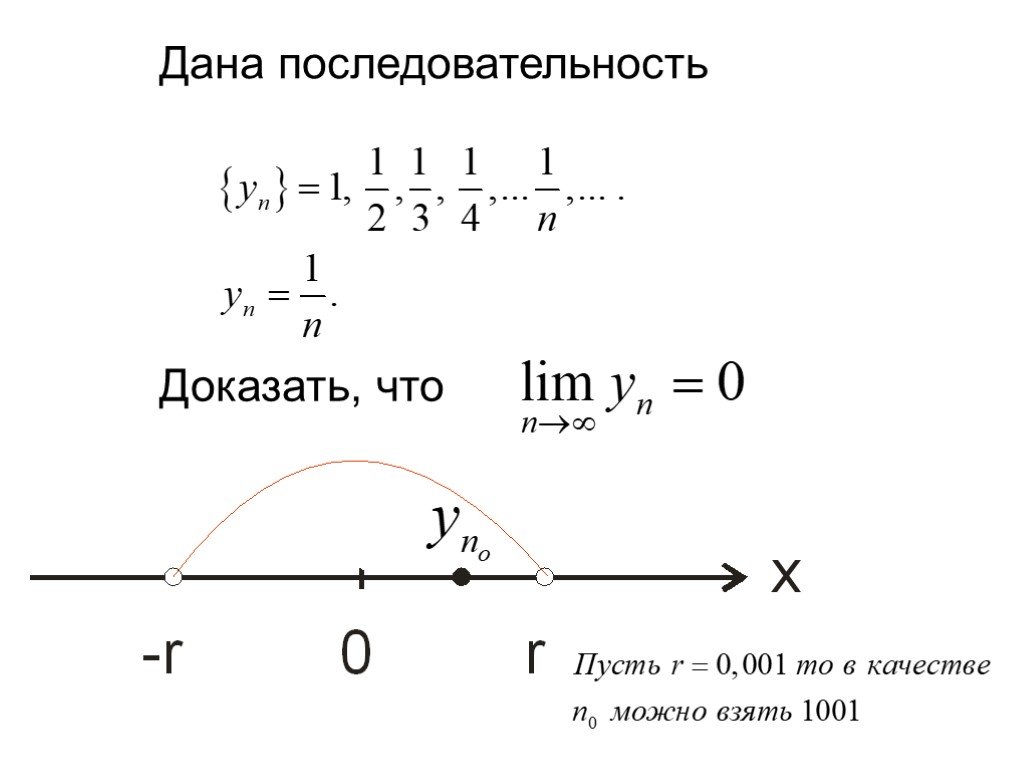
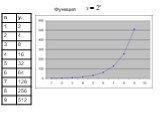
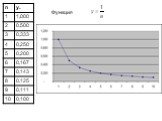
f(x)=x+2, при х 1. f(0,9)=2,9 f(0,99)=2,99 f(0,999)=2,999 f(1,1)=3,1 f(1,01)=3,101. Определение. Постоянная величина а называется пределом переменной ...Числовые последовательности
Что узнаете нового. Определение числовой последовательности Способы задания Стандартные упражнения. Последовательности. Угадайте закономерность. Способы ...Предел
Оглавление. Титульная страница Оглавление Вступление Предел переменной величины Основные свойства пределов Предел функции в точке Понятие о непрерывности ...Космос и математика
. Открытие космической эры. Открытие космической эры и начало освоения космического пространства - самое выдающееся достижение человечества XX в. ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Зачем нужна математика
Не хочу я математику учить. Складывать умею, умножать, делить. Сдачу в магазине сосчитаю, Хватит знаний этих, точно знаю. Мне задачи больше не нужны. ...Конкурс "Ох, уж эта математика"
Зал красочно оформлен: на стенах математические газеты. Рисунки, кроссворды, высказывания ученых. Их портреты. В жюри трое родителей. Ведущая Счетный ...Занимательная математика в младших классах
Круглый, румяный. В печке печён, На окошке стужён. Кто я? Колобок. Проверка 5, 8, 4, 6, 7, 0, 1, 2 Молодцы! Задача. Семь снегирей на ветке сидели. ...Конспекты
Определение числовой функции. Область определения, область значений функции
Муниципальное общеобразовательное учреждение. Оковецкая средняя общеобразовательная школа. Селижаровский район Тверская область. Тема урока:. ...Определение числовой функции. Виды. Свойства, графики числовых функций. Способы задания функции
Кейс технологии. Урок алгебры. . Калинина Ирина Борисовна. учитель математики. МАОУ ГИМНАЗИЯ №8 г. Перми. РАЗРАБОТКА УРОКА. c. применением ...Предел функции в точке, свойства. Бесконечно большие и бесконечно малые функции. Непрерывность функции
Министерство образования и науки Самарской области. . ГБОУ СПО «Безенчукский аграрный техникум». Конспект занятия. ТЕМА. Предел функции ...Предел функции в точке
Урок алгебры в 10 классе по теме «Предел функции в точке». Цель урока:. формирование у учащихся наглядно – интуитивных представлений о пределе ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 сентября 2018
Категория:Математика
Содержит:54 слайд(ов)
Поделись с друзьями:
Скачать презентацию