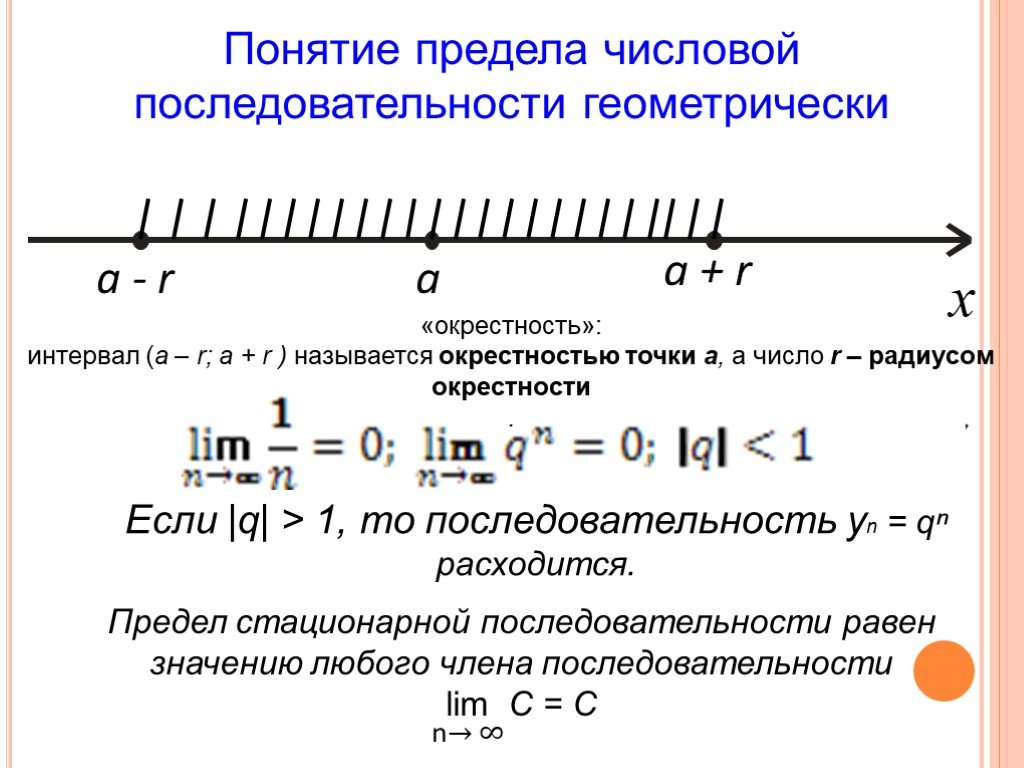
Презентация "Предел последовательности чисел" по математике – проект, доклад
Презентацию на тему "Предел последовательности чисел" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Закон больших чисел и Центральная предельная теорема
5. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2002. – 405 с. 6. Гмурман В.Е. Руководство к решению задач по теории ...Запись и название чисел до 20. Сложение и вычитание в пределах 20 без перехода через десяток
1 9 6. Разгадайте кроссворд. 2 4 5 О Т Р Е З О К Н О Л Ь С Е М Ь Л О М А Н А Я О Д И Н С У М М А. 1.Часть прямой, ограниченная с двух сторон точками. ...Нумерация чисел в пределах 10
Сказка «Путешествие по стране Цифирии». 1 — крючок для одежды; 2 — лебедь в пруду; 3 — ласточка; 4 — перевернутый стул; 5 — серп; 6 — дверной замочек; ...Нумерация чисел в пределах 1000. Закрепление
436 = 400 + 30 + 6. 12 4 108 9. 400 15 16 300 100. 6 14 12. Задача 1. В отряде космонавтов было 96 мужчины, а женщин в 4 раза меньше. Сколько всего ...Определение чисел arcsina, arccosa,arctga, arcctga
План. Теорема о корне монотонной функции Возрастание синуса на отрезке [−π/2; π/2] Определение арксинуса числа График синуса на отрезке [−π/2; π/2] ...Нумерация чисел в пределах 1000
Чтоб водить корабли, Чтобы в небо взлететь, Надо многое знать, Надо многое уметь. И при этом, и при этом, Вы заметьте-ка, Очень важная наука – МА-ТЕ-МА-ТИ-КА! ...Магия чисел
Цель исследования Исследовать влияние числа на судьбу человека. 2. Задачи Рассмотреть взаимосвязь между судьбой известных личностей и трактовкой числа ...Мир чисел
Наша цель :. -как попасть в этот мир? -велик ли он? -сколько в нём жителей? -знакомы ли мы с ними? Этапы работы:. Создание рукописи ( работа в библиотеке) ...История натуральных чисел
История чисел. Цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 иногда по ошибке называют «арабскими». Дело в том, что существовала индийская система нумерации, ...История чисел и системы счисления
Содержание. Понятие «системы счисления» История чисел Виды систем счисления Непозиционные системы счисления Позиционные системы счисления Арабская ...Округление натуральных чисел
Пример: 564≈560. Знак ≈ читается как «приближенно равно». Приближенное значение с недостатком. Пример: 423 ≈ 420 Число 420 - приближенное значение ...В мире чисел
Корни нумерологии. 1. Качества: благость, желательность, необходимость, неделимость. Связывалась с Аполлоном, Прометеем Символизирует начинание, источник, ...Вычитание отрицательных и положительных чисел
Тип урока: Урок усвоения новых знаний. Ход урока: 1)Организационный момент 2) Повторение 3)Актуализация знаний (в тетрадях) 4) Фиксация затруднения ...Обозначение множества натуральных чисел
Какие числа называются натуральными? Числа, которые применяются для счета предметов называются натуральными. 5 14 1. ЦИФРЫ. Любое натуральное число ...Вычитание двузначных чисел
16-7=9. 15-7 12-7 11-9 12-3 12-8 11-8 15-8 15-9 и в а н у ш к. 74-12 65-22 41-24 76-9. Алгоритм. Пишу единицы под единицами, а десятки – под десятками. ...Вычитание натуральных чисел и его свойства
Цели:. Усвоить понятие действия «вычитания» и его свойства; закрепить умение вычитать многозначные числа. 5 - 4 = 1 Уменьшаемое Вычитаемое Разность. ...Вычитание двузначных чисел
НОВОЕ ЗНАНИЕ (понятие, способ действия) и его фиксация (эталон). Алгоритм вычитания двузначных чисел с переходом через разряд. ПРОБНОЕ ДЕЙСТВИЕ. Найти ...Всё об округлении чисел
Содержание. Что такое «округление числа» Округление целых чисел Округление десятичных дробей Для самостоятельного решения. Определение. Округление ...Влияние "главных чисел" на характер человека
Эпиграф. Мысль выражать все числа знаками настолько проста, что именно из – за этой простоты сложно осознать, сколь она удивительна. Пьер Симон Лаплас. ...Нахождение числа по его процентам. Нахождение процентного отношения двух чисел
Домашнее задание. № 6.40 1) 8; 3) 5,6 ; 2) 48; 4) 4 . № 6.46 2) 20 % ; 3) 10 % ; 4 ) 1000% . Выразить проценты в виде десятичной дроби? 20% 75% 125% ...Конспекты
Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице
Тема:. Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице. 5 класс специальной (коррекционной) школы. Цели:. . . Познакомить ...+ двухзначных и однозначных чисел в пределах 100
УРОК МАТЕМАТИКИ. Тема:. + двухзначных и однозначных чисел в пределах 100 (урок обобщения). Цель:. Создание условий для формирования УУД при ...Нумерация чисел в пределах 20
Технология развивающего обучения. . . . . . . МБОУ Добринская ООШ. . Учитель Силаева Г.М. ...Нумерация целых неотрицательных чисел в пределах тысячи
Конспект урока. Ф.И.О. учителя:. Дьяченко Наталья Сергеевна. Название урока:. математика. Тема урока:. «Нумерация ...Выполнение сложения и вычитания двузначных чисел столбиком в пределах 100
. . Согласованно. Зам.директора по УВР. ______Кострюкова И.А. . Утверждаю. Директор школы:. _______ Дядькина Л.В. . Муниципальное образовательное ...Десяток. Состав чисел в пределах 10. Прямоугольник
МКС(К)ОУ для обучающихся, воспитанников с ограниченными возможностями здоровья Еманжелинская специальная (коррекционная) школа-интернат VIII вида. ...Закрепление приемов письменного сложения и вычитания чисел в пределах 1000
Уникальность 76%. Закрепление приемов письменного сложения и вычитания чисел в пределах 1000. . Цели:. 1. Закреплять навыки вычислений в пределах ...Закрепление приемов письменного сложения и вычитания чисел в пределах 1000
Конспект урока математики по теме " Закрепление приемов письменного сложения и вычитания чисел в пределах 1000" для 3 класса Сидорова Альбина Фердинандовна ...Вычитание чисел в пределах 1000 с переходом через разряд
. . . . . . . . . Тема урока:. Вычитание чисел в пределах 1000 с переходом через разряд. Цель урока. : формировать умение ...закрепление письменного сложения и вычитания двузначных чисел в пределах 100
Тема урока: закрепление письменного сложения и вычитания двузначных чисел в пределах 100. Цели урока: • повторить и закрепить письменное сложение ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 июня 2019
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию