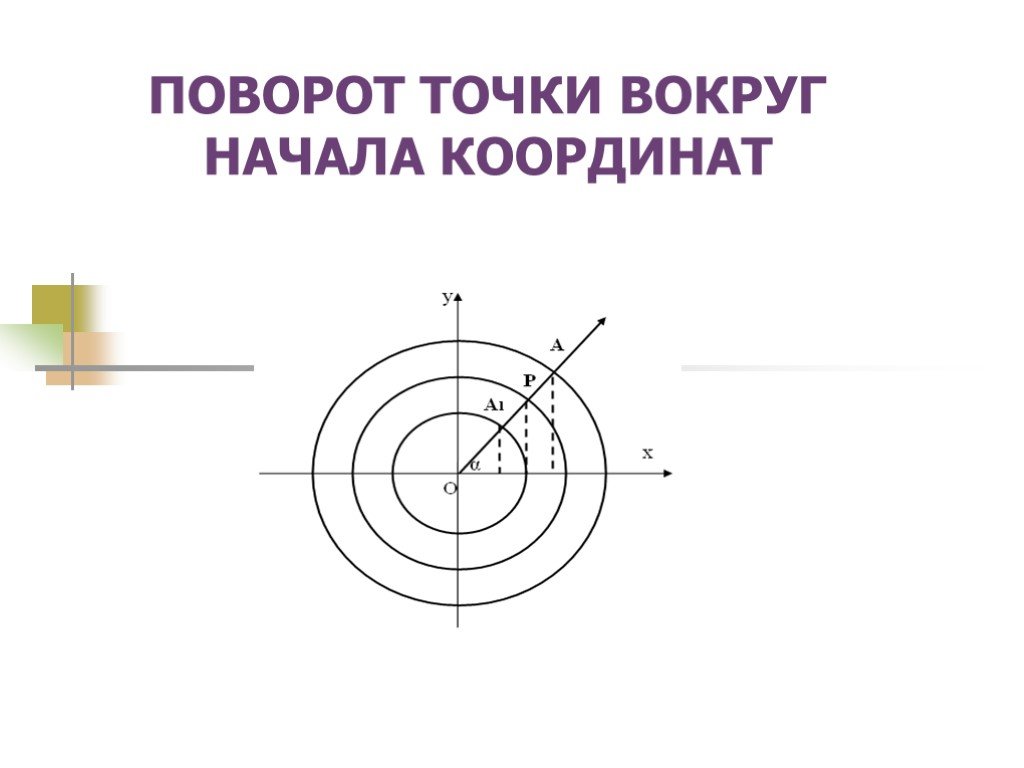
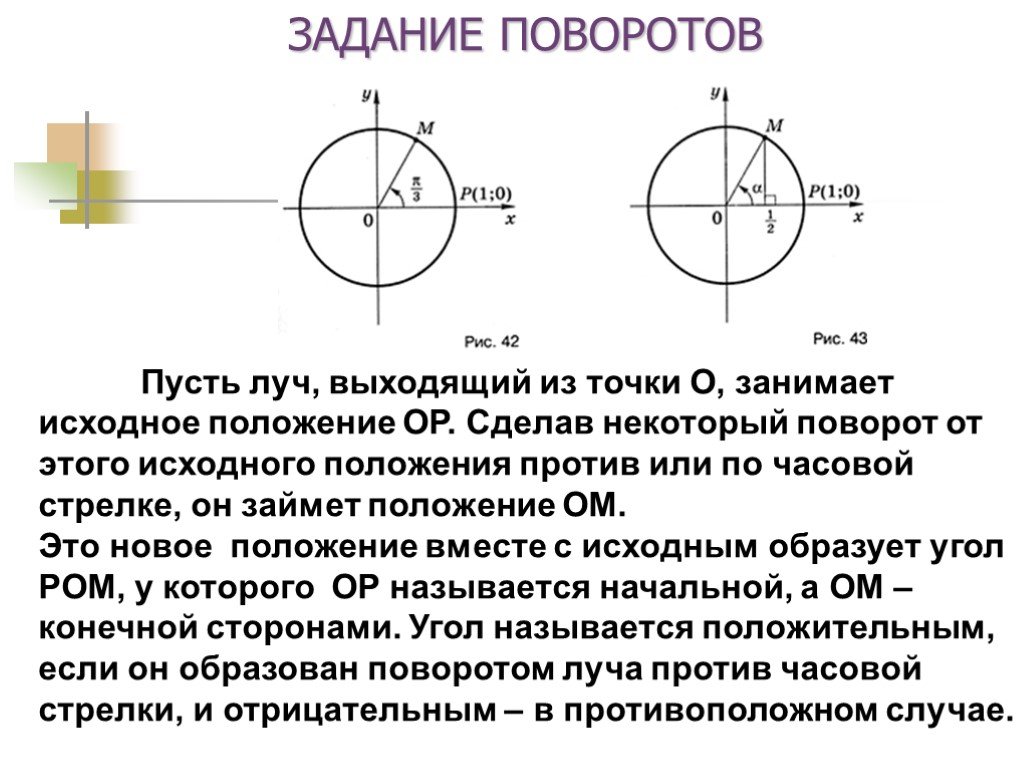
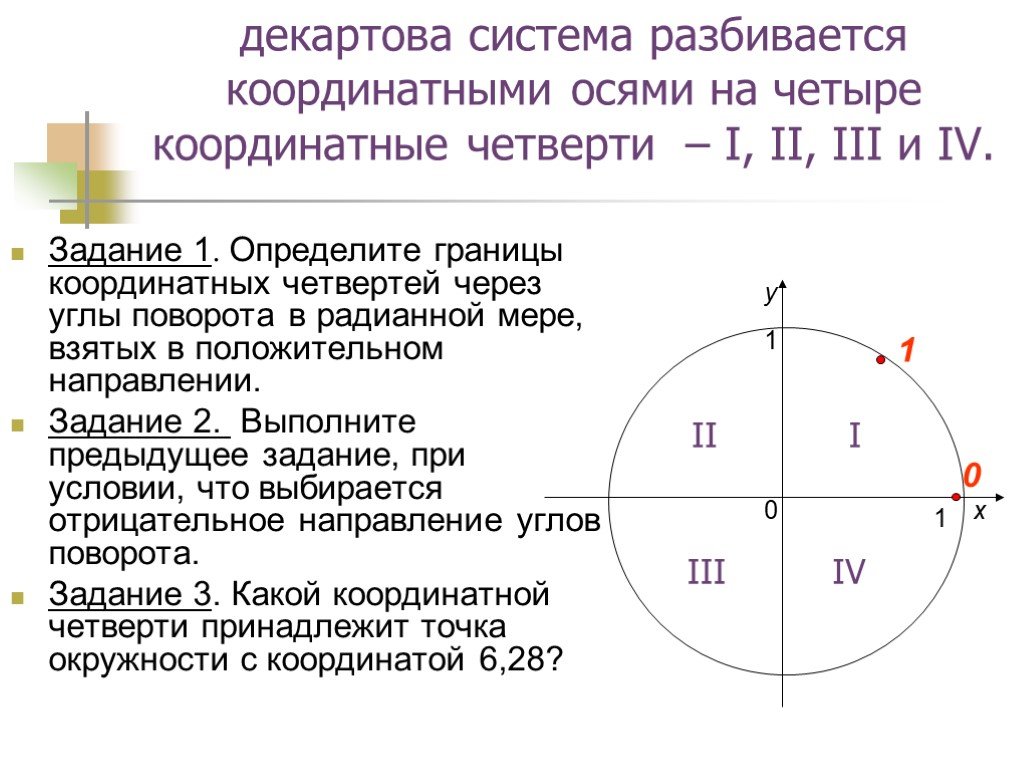
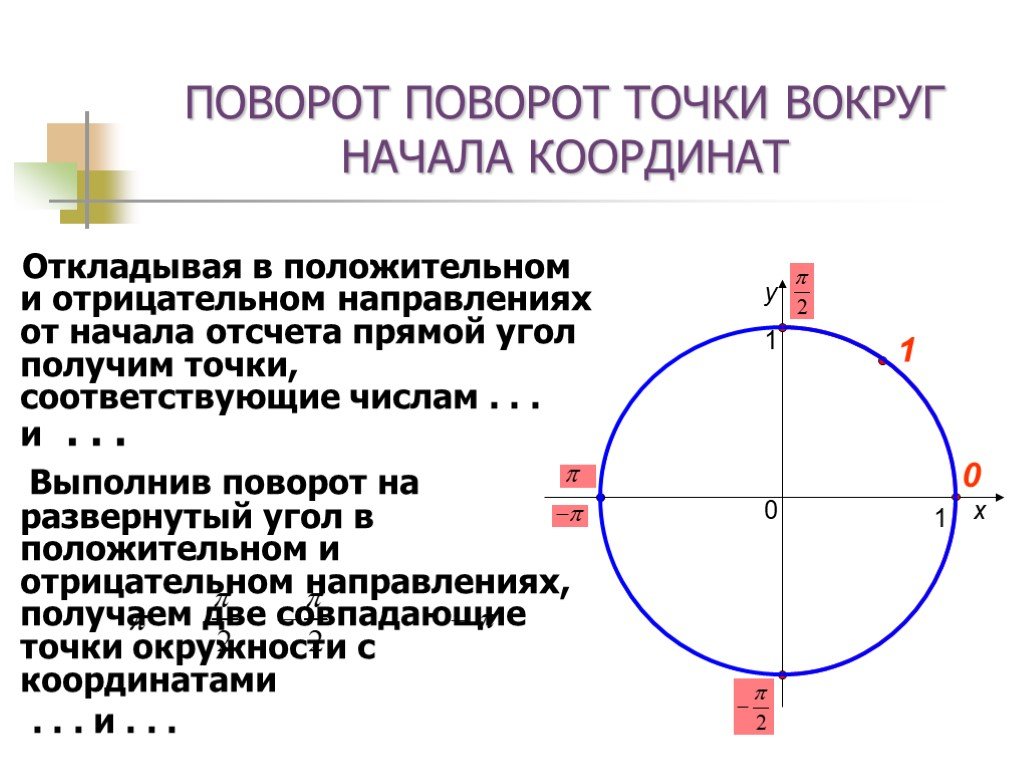
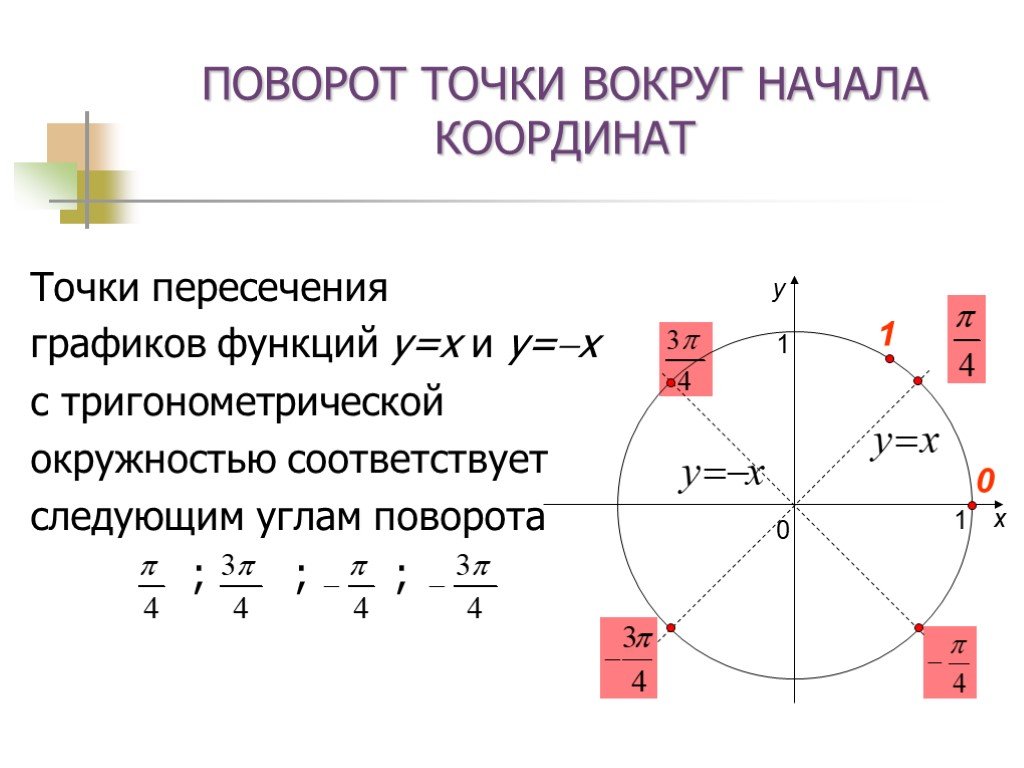
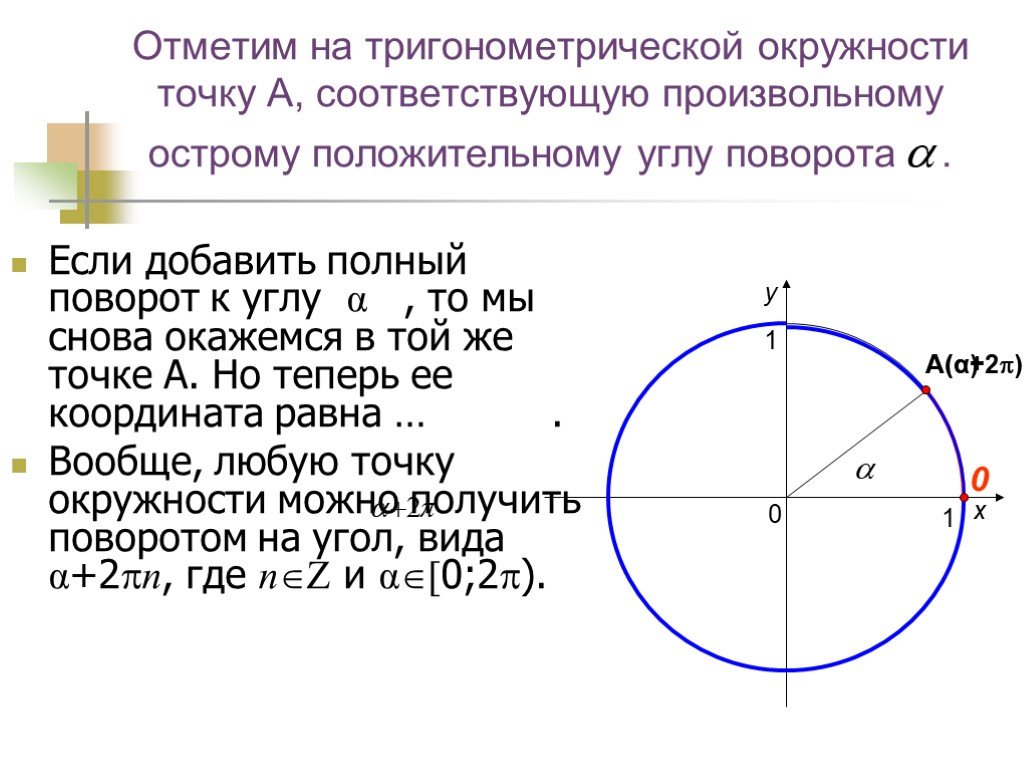
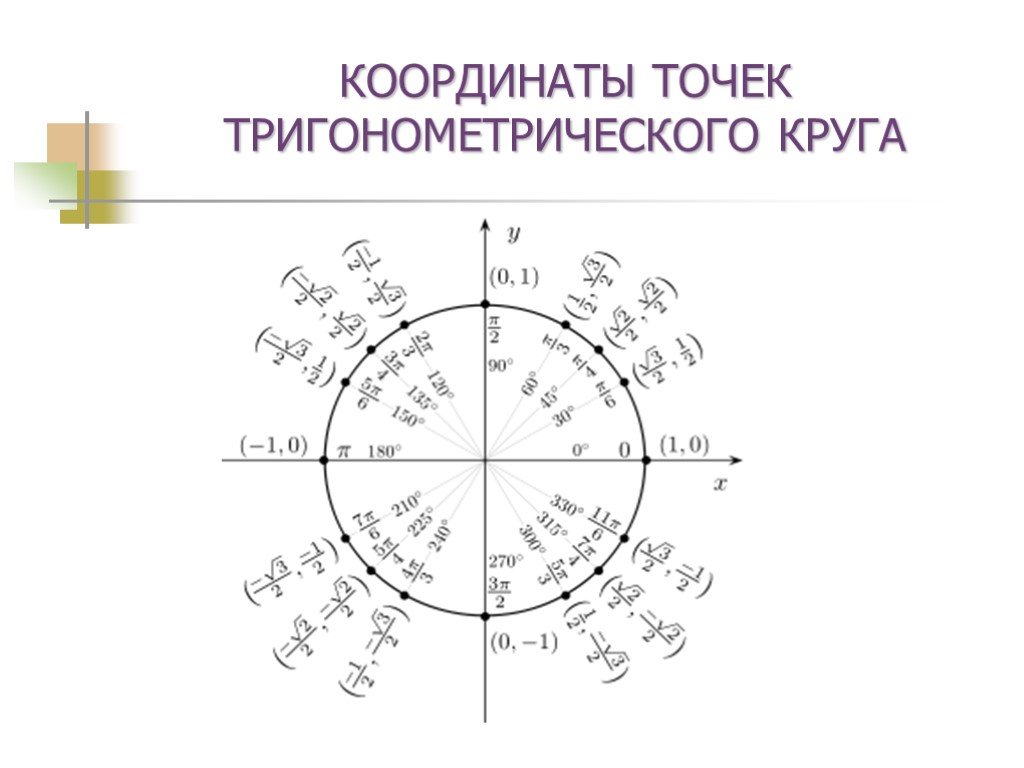
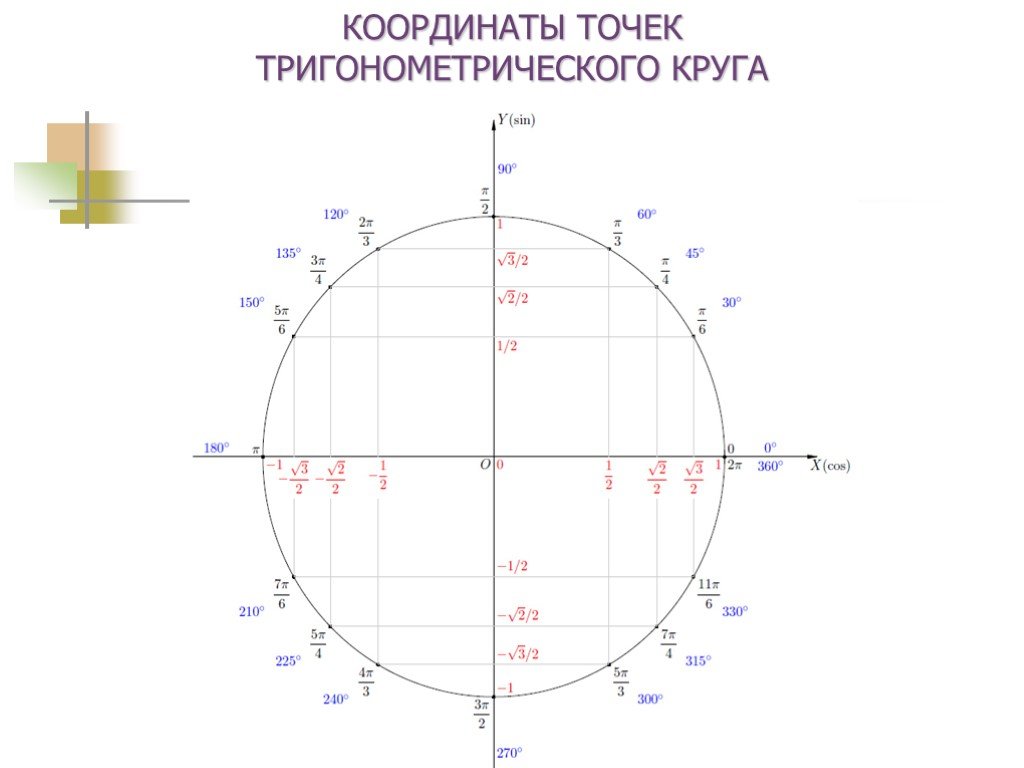
Презентация "Поворот точки вокруг начала координат" по математике – проект, доклад

ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ

Зачатки тригонометрических познаний зародились в древности

Николай КОПЕРНИК (1473 – 1543)

Франсуа ВИЕТ (1540 - 1603)

Евклид (ок. 325 – 265 до н.э.)

Тригонометрия являлась вспомогательным разделом астрономии

Иоганн КЕПЛЕР (1571 – 1630)

Исаак НЬЮТОН (1643 – 1727)

Готфрид ЛЕЙБНИЦ (1646 – 1716)

С факелом тригонометрии доказывали движение планет, пути комет и приливы океанов

ЗАДАНИЕ ПОВОРОТОВ Пусть луч, выходящий из точки О, занимает исходное положение ОР. Сделав некоторый поворот от этого исходного положения против или по часовой стрелке, он займет положение ОМ. Это новое положение вместе с исходным образует угол РОМ, у которого ОР называется начальной, а ОМ – конечной сторонами. Угол называется положительным, если он образован поворотом луча против часовой стрелки, и отрицательным – в противоположном случае.

декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и IV.

Задание 1. Определите границы координатных четвертей через углы поворота в радианной мере, взятых в положительном направлении. Задание 2. Выполните предыдущее задание, при условии, что выбирается отрицательное направление углов поворота. Задание 3. Какой координатной четверти принадлежит точка окружности с координатой 6,28?

x y 0 1 I II III IV

ПОВОРОТ ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ

Откладывая в положительном и отрицательном направлениях от начала отсчета прямой угол получим точки, соответствующие числам . . . и . . . Выполнив поворот на развернутый угол в положительном и отрицательном направлениях, получаем две совпадающие точки окружности с координатами . . . и . . . .

Точки пересечения графиков функций y=x и y=x с тригонометрической окружностью соответствует следующим углам поворота ; ; ;

Отметим на тригонометрической окружности точку А, соответствующую произвольному острому положительному углу поворота .

Если добавить полный поворот к углу α , то мы снова окажемся в той же точке А. Но теперь ее координата равна … . Вообще, любую точку окружности можно получить поворотом на угол, вида α+2n, где n и α[0;2).

A(α) A(α+2)

КООРДИНАТЫ ТОЧЕК ТРИГОНОМЕТРИЧЕСКОГО КРУГА