Презентация "Прямоугольная система координат" по математике – проект, доклад
Презентацию на тему "Прямоугольная система координат" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
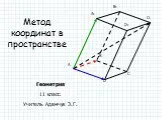
Прямоугольная система координат в пространстве
Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Ох – ось абсцисс, Оу – ось ординат, Оz ...Прямоугольная система координат
Прямоугольная система координат Наумова М.Н. – учитель математики МОУ «Корниловская средняя школа», Архангельская обл., Верхнетоемский р-н, п. Двинской. ...Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве. Проведем через точку пространства три попарно перпендикулярные прямые, на каждой из них выбрано направление(обозначается ...Прямоугольная система координат на плоскости
Я знаю, что вам очень понравилась тема «Координатная плоскость» Давайте проверим, хорошо ли вы ее помните. Вспомни: Что такое координатная плоскость? ...Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости. Цель урока: - ознакомиться с прямоугольной системой координат на плоскости; -определять координаты точки, ...Прямоугольная декартова система координат
Тем, кто любит математику, Тем, кто знает математику, Тем, кто ещё не знает, Что он любит математику И тем, кто других учит математике Предназначена ...Декартова система координат на плоскости
Зададим на плоскости две оси координат, расположив их под прямым углом друг к другу:. О – точка пересечения осей х и у, начальная точка системы координат. ...Декартова система координат на плоскости
Декартова система координат на плоскости. Мыслю, следовательно существую Декарт. Вступление. Одна из ярких страниц VΙΙ века связана с работами французского ...Система координат в пространстве
Вспомним, как определяется координатная(числовая) прямая. Изображаем произвольную прямую;. х 0 1 М а. Тогда любой точке этой координатной прямой соответствует ...Является ли система координат чисто математическим понятием
Цели и задачи исследования . Выяснить , где еще кроме математики применяется система координат Разобраться как используют систему координат моряки ...Система координат на плоскости
Кто открыл прямоугольную систему координат? Знакомы ли вы с историей возникновения координат? Гиппарх Птолемей Рене Декарт. Что называется системой ...Система координат
Известно, что:. для определения положения точки на земной поверхности надо знать ее географические координаты. место в зрительном зале тоже определяется ...Система координат в пространстве
Работу выполнила: Кошкарева Галина Фёдоровна Учитель высшей квалификационной категории, МОУ – средняя общеобразовательная школа № 14 Города Искитима, ...Задания на определение координат
х у 0 1 А Повторяем устно. 1.Определите координаты векторов. 2. Как определить координаты точки, зная координаты её радиус-вектора? 3. Как определить ...Римская система счисления
Цель работы:. Познакомиться с историей возникновения и развития римской системы счисления Познакомиться с правилами составления чисел римской системы ...Сдвиг графика функции y = x вдоль осей координат
y = x2 y = x2 - 2 y = x2 + 4 y x 1 3 4 -1 В.П. (0;0) В.П. (0;-2) В.П. (0;4). Задание 1. Укажите координаты вершины параболы, которая получена сдвигом ...Двоичная система счисления
Вильгельм Готфрид Лейбниц (1646-1716). Медаль, нарисованная В. Лейбницем в 1697 г., поясняющая соотношение между двоичной и десятичной системами исчисления. ...Меры и метрическая система
МЕРА ЛАДОНЬ. МЕРА ПАЛЕЦ. МЕРА ФУТ. КНЯЗЬ ТАЙЛЕРАМ. Д.М. МЕНДЕЛЕЕВ. Б. С. ЯКОБИ. . УГОЛОК МЕНДЕЛЕЕВА. ПРИЕР ДЮВЕРНУА. Д.М. ПЕРЕВОЩИКОВ. АРХИВНЫЙ МЕТР. ...Метод координат в пространстве
Цели урока:. 1.Повторить понятия вектора; 2.Ввести понятие прямоугольной системы координат в пространстве. Задачи урока: выработать умения строить ...Десятичная система счисления
Числа, которые могут быть получены в результате счета предметов-1,2,3,45 и т.д., называют натуральными. Числа 1,2,3,4,5,6,7,8,9, 0 называют арабскими. ...Конспекты
Прямоугольная система координат в пространстве
Государственное образовательное учреждение. . начального профессионального образования. «Профессиональное училище №5» г. Белгорода. ...Координатная плоскость. Прямоугольная система координат
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ «ОТДЕЛ ОБРАЗОВАНИЯ, ФИЗИЧЕСКОЙ КУЛЬТУРЫ И СПОРТА г. ШАХТИНСКА». КОММУНАЛЬНОЕ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ «ОБЩЕОБРАЗОВАТЕЛЬНАЯ ...Прямоугольная система координат
Разработка уроков. по теме «Прямоугольная система координат». . 6 класс. Разработала: Скилевая Елена Владимировна. ...Формы представления информации. Метод координат
Автор:. Коджамонян Оксана Игоревна. Должность. : учитель информатики. Место работы. : МБОУ СОШ 30 посёлка Молодёжного муниципального образования ...Применение метода координат к решению задач
Геометрия в 11 классе Ковтун В.В.учитель математикиМосковский район Санкт-Петербург. Тема урока:. Применение метода координат к решению задач. ...Построение фигур по заданным координатам в системе координат
Тема урока: «Построение фигур по заданным координатам в системе координат». Учитель математики ГБОУ СОШ №1968. Урок комплексного применения знаний. ...Построение графика квадратичной функции с использованием сдвигов по осям координат
МБОУ Чистопольская СОШ. Урок алгебры в 8 классе. Тема «Построение графика квадратичной функции с использованием сдвигов по осям координат». ...Метод координат на плоскости. Координаты на прямой
Муниципальное бюджетное общеобразовательное учреждение. «Вечерняя сменная средняя общеобразовательная школа при ИУ». Конспект урока. Метод координат ...Контрольная работа по теме «Использование метода координат в пространстве для решения заданий С2 ЕГЭ
Конспект урока по теме «. Контрольная работа по теме «Использование метода координат в пространстве для решения заданий С2 ЕГЭ»». Автор:. Макарова ...Закрепление изученного материала. Солнечная система
Открытый урок математики во 2–в классе. Тема:. Закрепление изученного материала. Солнечная система. Цели урока:. Познакомить с планетами Солнечной ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:27 апреля 2019
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию