Презентация "Комбинаторные задачи" (5 класс) по математике – проект, доклад
Презентацию на тему "Комбинаторные задачи" (5 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
Комбинаторные задачи и их решения
1) Цели и задачи 2) Пояснительная записка 3) Требования к уровню подготовки 4) Учебно– тематический план 5) Содержание программы 6) Поурочное планирование ...Комбинаторные задачи Тема «Введение в вероятность»
Комбинаторика. В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов ...Комбинаторные задачи
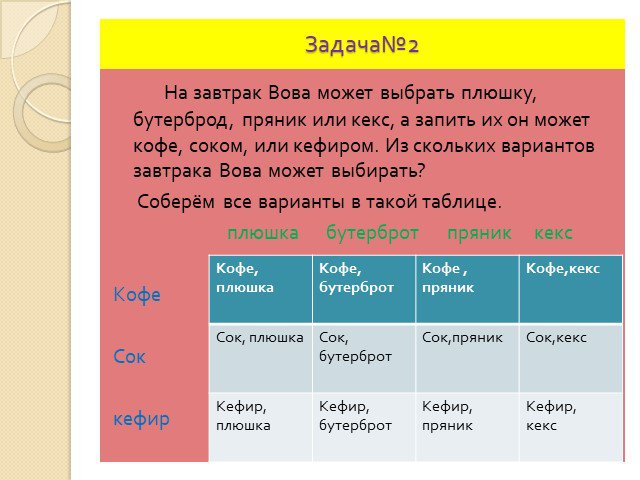
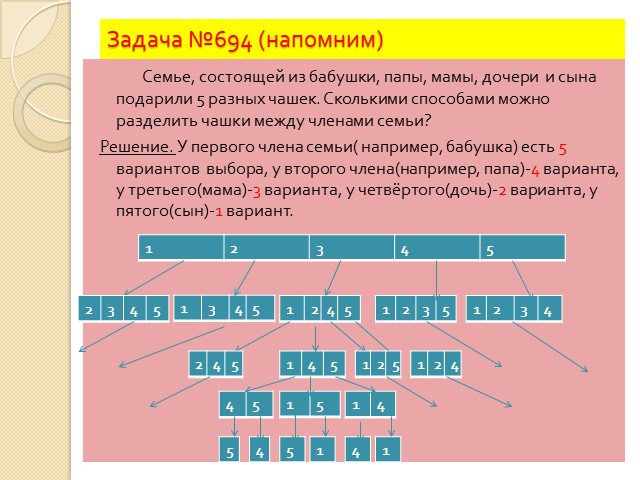
Решение задач. Перестановки Размещения Сочетания. Простейшие комбинации. . Правило умножения! Если элемент А можно выбрать m способами, а элемент ...Комбинаторные задачи
Тема занятия«Комбинаторные задачи». Цель : -повторить способы решения комбинаторных задач; - защитить минипроекты по теме «Комбинаторные задачи». ...Комбинаторные задачи. Правило умножения
Образовательные цели:. 1) Сформировать умение проводить самоконтроль знания алгоритма решения комбинаторных задач правилом умножения и умения его ...Комбинаторные задачи
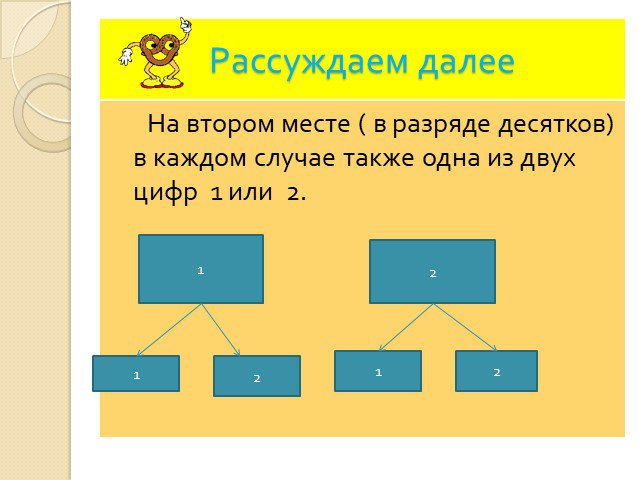
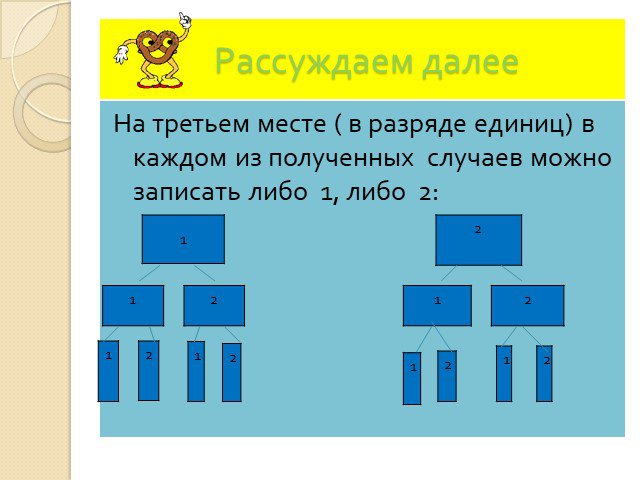
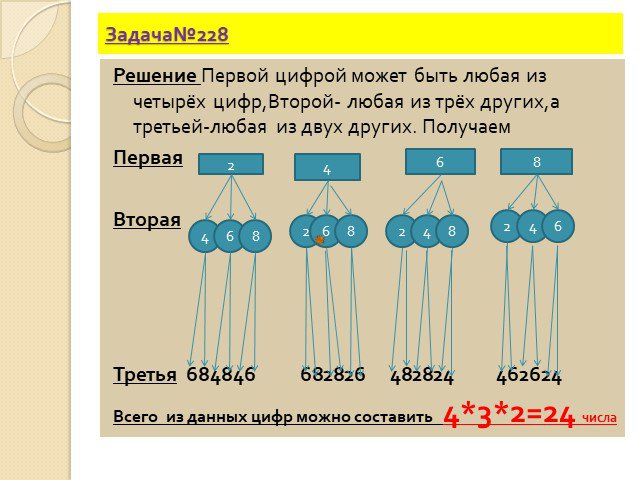
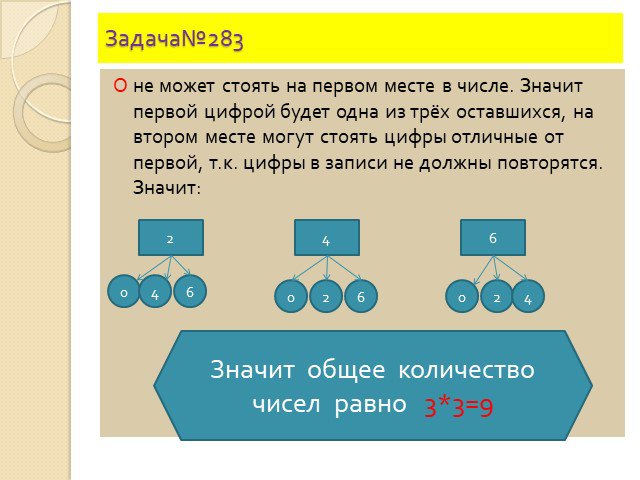
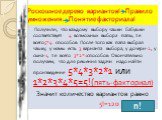
Дерево возможных вариантов. 4 7. №18.4. №18.7. № 18.9(а-в). Методы решения комбинаторных задач. 1.Метод перебора. 2.Составление дерева возможных вариантов. ...Комбинаторные задачи: размещения
Запомните Определение:. Размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним ...Комбинаторные задачи: перестановки
Вычислите : 10. Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять ...Взаимообратные задачи
Условие Вопрос Схема Выражение Решение Ответ. На кормушке сидело 2 синички. Прилетела ещё 1синичка. Сколько синичек прилетело? На кормушке сидело ...Анания Ширакаци и его задачи
Дата рождения: около 610 год Место рождения: в области Ширак провинции Айрарат Дата смерти: около 685 год Научная сфера: математик, астроном, географ. ...Вводные задачи
Задачи на чередование. 1.На плоскости располо- жено 11 шестеренок,со- единенных по цепочке. Могут ли все шестеренки вращаться одновременно? Ответ:нет.Если ...Основные задачи на проценты
1. Дробь 1/5 равна А) 20% Б) 30% В) 50%. назад. Может подумаешь еще? . 2. 30% от числа 800 равно. А) 24 Б) 240 В) 2400. . . 3.У нас в школе есть участок ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Математические задачи от русских, советских и зарубежных писателей
Можно ли изучать математику в школе, используя произведения русских, советских и зарубежных писателей? «Гуманитарные науки... только тогда будут удовлетворять ...Геометрические задачи типа «С4»
Задачи Желаю успеха! "Дорогу осилит идущий!". Помните:. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС так, что BD:DC = 3:8. ...Геометрические задачи со спичками
1. Уберите 4 спички так, чтобы осталось 4 маленьких и 1 большой квадраты. Ответ :. 2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, ...Геометрические задачи с практическим содержанием
введение. Решение геометрических задач с практическим содержанием позволяет: усилить практическую направленность изучения школьного курса геометрии; ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Геометрические задачи на построение
Задачи на построение. Окружность Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже ...Геометрические задачи «С2»
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. ...Конспекты
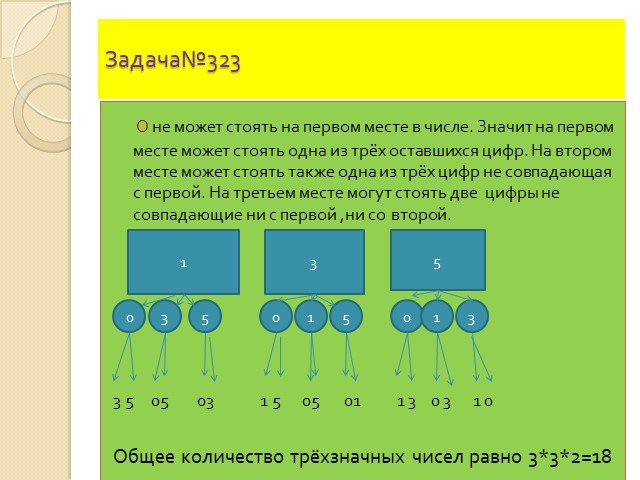
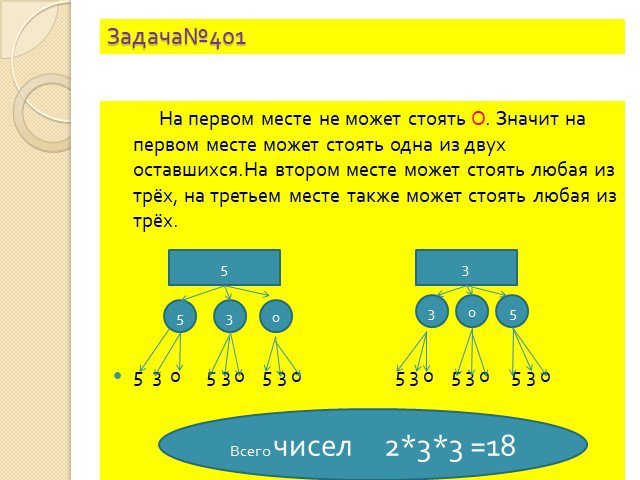
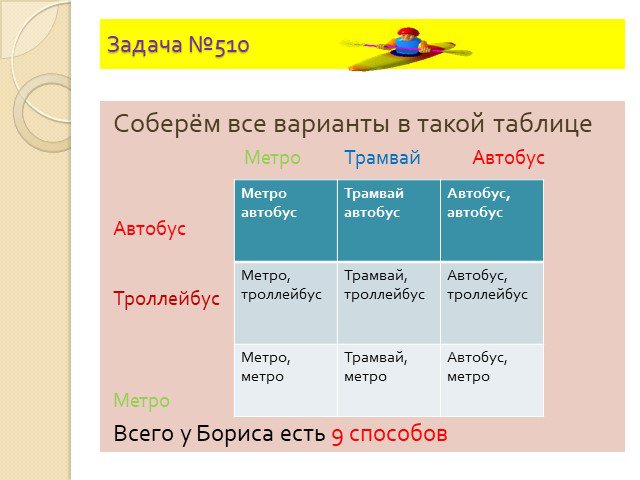
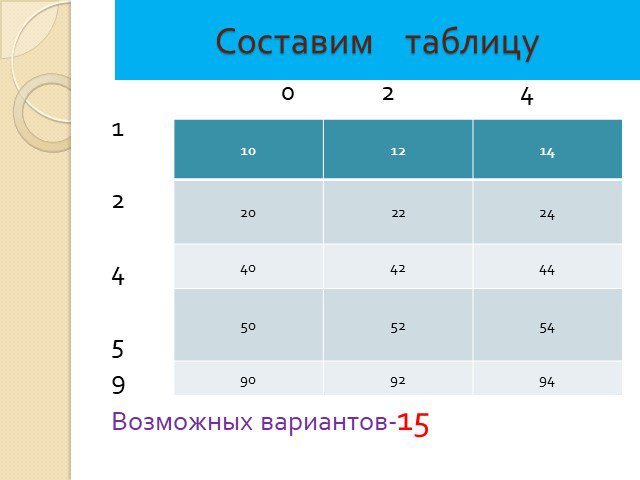
Комбинаторные задачи
Технологическая карта урока математики. Тема урока: « Комбинаторные задачи». Класс:6. Учитель: Калинина Ольга Владимировна. Тип урока: Урок открытия ...Комбинаторные задачи
Урок – изучение нового материала. (Оформление параллельное с отдельным описанием УУД и объединением колонки визуального ряда с колонками деятельности ...Комбинаторные задачи
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА УРОКА В 5 КЛАССЕ«Комбинаторные задачи». . ФИО (полностью). . Сукманова Светлана Валентиновна. . . ...Развивающие задачи
МЕТОДИЧЕСКАЯ РАБОТА. «Развивающие задачи в 5-х классах». Учителя математики высшей квалификационной категории. Васильевой Н. И. ГБОУ СОШ № ...Простые и составные задачи
Тема урока:. Простые и составные задачи. Цель: знакомство с понятиями простая и составная задача, выявление существенных признаков этих понятий. ...Простые арифметические задачи на разностное сравнение
Тема урока. : «Простые арифметические задачи на разностное сравнение». Тип урока. : урок выработки умений и навыков (применение знаний в новых ситуациях). ...Взаимно обратные задачи
Математика. Тема:. Взаимно обратные задачи. Цель:. Сформировать представление о взаимно обратных задачах, умение их распознавать и составлять задачи ...Упражнения и задачи на усвоение таблицы деления на 2. Закрепление
Урок математики во 2 классе. Тема: Упражнения и задачи на усвоение таблицы деления на 2. Закрепление . . Урок - закрепление. Цели:. -Воспроизводить ...Статистическое определение вероятности. Комбинаторные методы решения задач
Алгебра. Раздел: Теория вероятностей. Тема:. Статистическое определение вероятности. Комбинаторные методы решения задач. Цель:. выработать умение ...Решение задачи исследовательского характера
Лукашова Маргарита Александровна, учитель математики МБОУ г. Мурманска лицей №4. . Предмет: математика. Возраст детей: 7 класс. Место проведения: ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 марта 2016
Категория:Математика
Классы:
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию