Презентация "Комбинаторные задачи: перестановки" по математике – проект, доклад
Презентацию на тему "Комбинаторные задачи: перестановки" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
Комбинаторные задачи
Тема занятия«Комбинаторные задачи». Цель : -повторить способы решения комбинаторных задач; - защитить минипроекты по теме «Комбинаторные задачи». ...Комбинаторные задачи и их решения
1) Цели и задачи 2) Пояснительная записка 3) Требования к уровню подготовки 4) Учебно– тематический план 5) Содержание программы 6) Поурочное планирование ...Комбинаторные задачи
Решение задач. Перестановки Размещения Сочетания. Простейшие комбинации. . Правило умножения! Если элемент А можно выбрать m способами, а элемент ...Комбинаторные задачи
Что такое комбинаторика? В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа ...Комбинаторные задачи: размещения
Запомните Определение:. Размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним ...Комбинаторные задачи
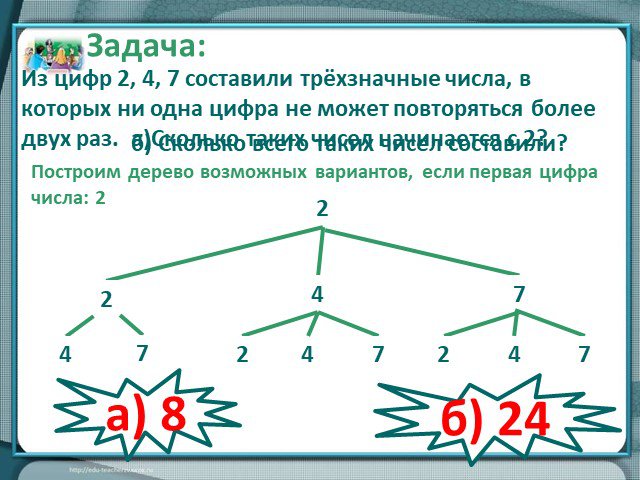
Дерево возможных вариантов. 4 7. №18.4. №18.7. № 18.9(а-в). Методы решения комбинаторных задач. 1.Метод перебора. 2.Составление дерева возможных вариантов. ...Комбинаторные задачи Тема «Введение в вероятность»
Комбинаторика. В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов ...Комбинаторные задачи. Правило умножения
Образовательные цели:. 1) Сформировать умение проводить самоконтроль знания алгоритма решения комбинаторных задач правилом умножения и умения его ...Логические задачи
Задача «Школьные учителя». В старших классах работают три учителя: Воронов, Соколов и Коршунов. Каждый из них преподает по два предмета, так что в ...Взаимообратные задачи
Условие Вопрос Схема Выражение Решение Ответ. На кормушке сидело 2 синички. Прилетела ещё 1синичка. Сколько синичек прилетело? На кормушке сидело ...Понятие задачи
О чем будет урок ? Задание 1. Правильный ответ А. Продолжаем размышлять… Задание 2. 1 ? 4. Задание 3 5. часть Думаем и отвечаем. . целое +. 4 + 1 ...Основные задачи на проценты
Как найти 1% от числа? 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти ...Олимпийские задачи на движение
Выполните устно. * Фигуристка произвольную программу откатала со скоростью 420м/ мин за 3 мин. Сколько метров проехала фигуристка за это время? * ...Наши задачи
На ярмарке браслет из драгоценных камней стоимостью 67рублей 35копеек. Переведите их в старинные меры денежных единиц. Как вы знаете, что каждый уважающий ...геометрия решение задачи
Дано: а-прямая, A B а Построить: BC=2AB Решение:. A,B-точки на прямой,. (на луче BA). Измерим циркулем расстояние между A и B,. отложим отрезок AC ...Геометрические задачи типа «С4»
Задачи Желаю успеха! "Дорогу осилит идущий!". Помните:. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС так, что BD:DC = 3:8. ...Геометрические задачи со спичками
1. Уберите 4 спички так, чтобы осталось 4 маленьких и 1 большой квадраты. Ответ :. 2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, ...Геометрические задачи с практическим содержанием
введение. Решение геометрических задач с практическим содержанием позволяет: усилить практическую направленность изучения школьного курса геометрии; ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Геометрические задачи на построение
Задачи на построение. Окружность Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже ...Конспекты
Комбинаторные задачи
Технологическая карта урока математики. Тема урока: « Комбинаторные задачи». Класс:6. Учитель: Калинина Ольга Владимировна. Тип урока: Урок открытия ...Комбинаторные задачи
Урок – изучение нового материала. (Оформление параллельное с отдельным описанием УУД и объединением колонки визуального ряда с колонками деятельности ...Комбинаторные задачи
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА УРОКА В 5 КЛАССЕ«Комбинаторные задачи». . ФИО (полностью). . Сукманова Светлана Валентиновна. . . ...Разбиение текста задачи на условие и вопрос
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 18». г. Абакана Республики Хакасия. ...Простые арифметические задачи на разностное сравнение
Конспект открытого урока по математике в 5 классе 8 вида. Тема урока. : «Простые арифметические задачи на разностное сравнение». Тип урока. ...Простые арифметические задачи на определение продолжительности, начала и конца события 7 класс
Простые арифметические задачи на определение продолжительности, начала и конца события. 7 класс. Цели урока:. - Формировать умения решать текстовые ...Учимся решать задачи
Тема. Решение задач. Цель. Формировать у детей умение решать составные задачи. Задачи. совершенствовать навыки в решении простых и составных ...Текстовые задачи с практическим содержанием
Котова Елена Васильевна. Учитель математики МОУ «Вейделевская СОШ». Тема урока: Текстовые задачи с практическим содержанием. Тип урока. : ...Составление краткой записи условия задачи
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2. им. А. А. Араканцева г. Семикаракорска». Конспект ...Решение задач. Обратные задачи
. . Урок математики 2 класса. Тема урока: Решение задач. Обратные задачи. Цель: . закрепить навык решения изученных задач. Задачи:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:17 января 2013
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию