Презентация "Логические задачи" по математике – проект, доклад
Презентацию на тему "Логические задачи" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 29 слайд(ов).
Слайды презентации
Список похожих презентаций
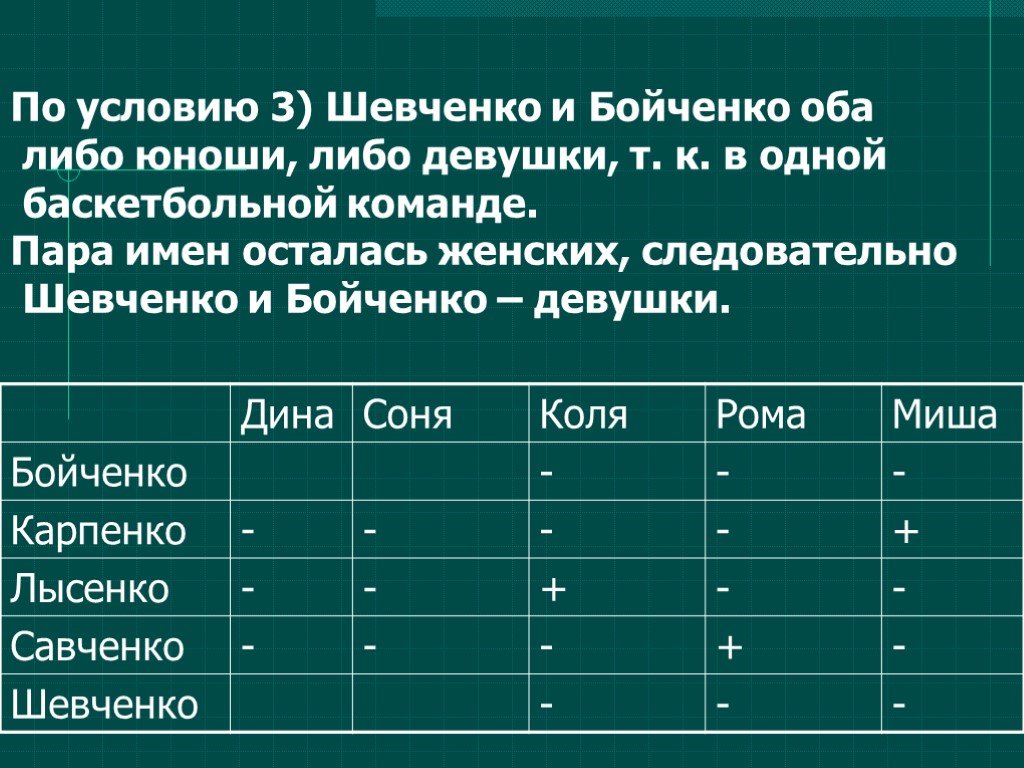
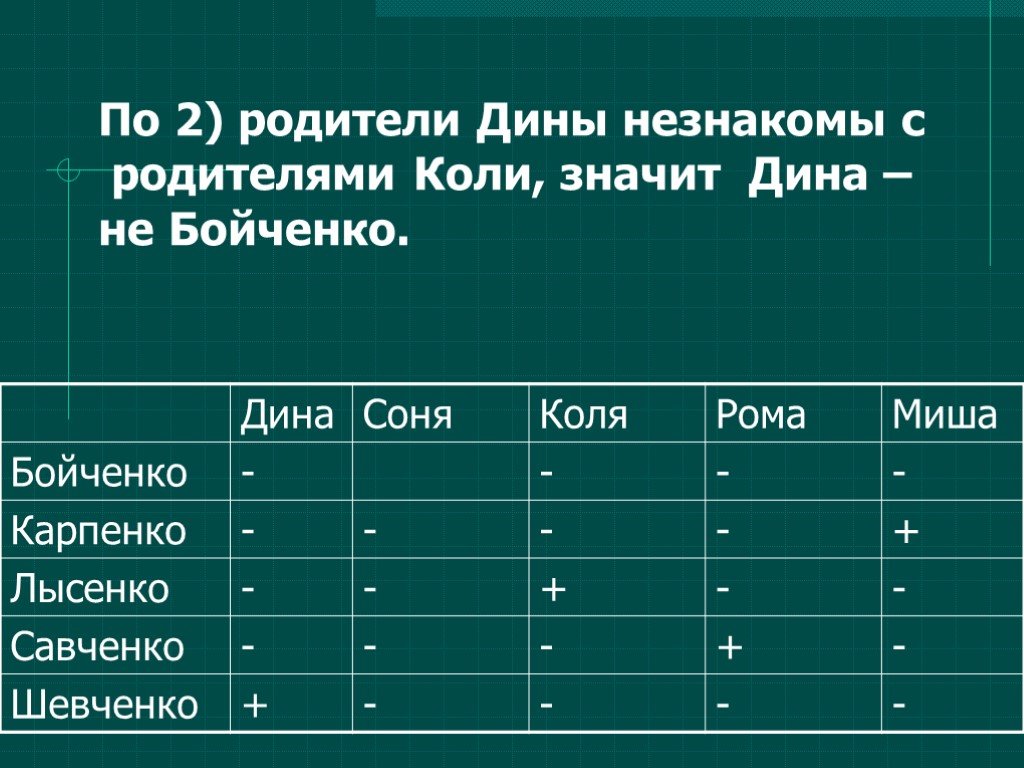
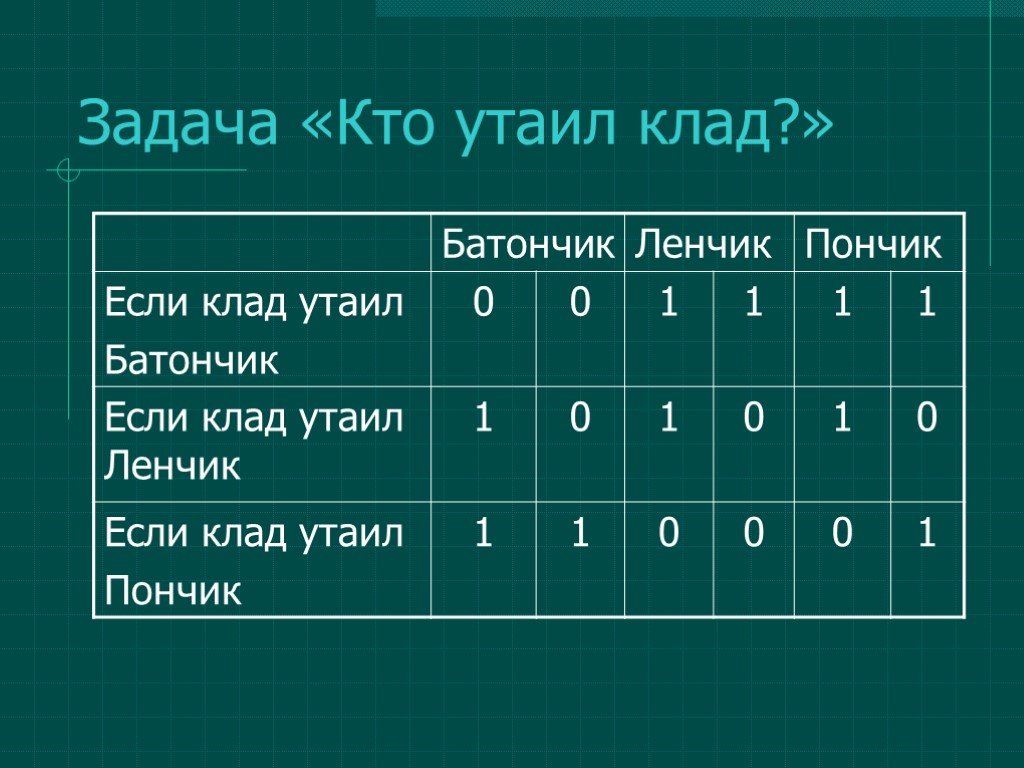
Логические задачи
Шесть школьников, участвуя в воскреснике, разбились на три брига-ды. Бригадиров звали: Володя, Петя, Вася. Володе с Мишей дали двухмет-ровые, Пете ...Логические задачи для 1 класса
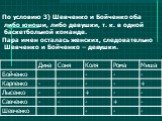
Дима выиграл у Алёши 2 партии в шахматы, а Алёша выиграл 3 партии. Сколько партий сыграли мальчики? задача 1 4 партии 5 партий 3 партии 1+1+1=3 2+1=3. ...Логические задачи для детей
В магазине было шесть разных ящиков с гвоздями. Масса ящиков в 6, 7, 8, 9, 10 ,11 кг. Два покупателя приобрели пять ящиков, причём каждому гвоздей ...Логические задачи и загадки
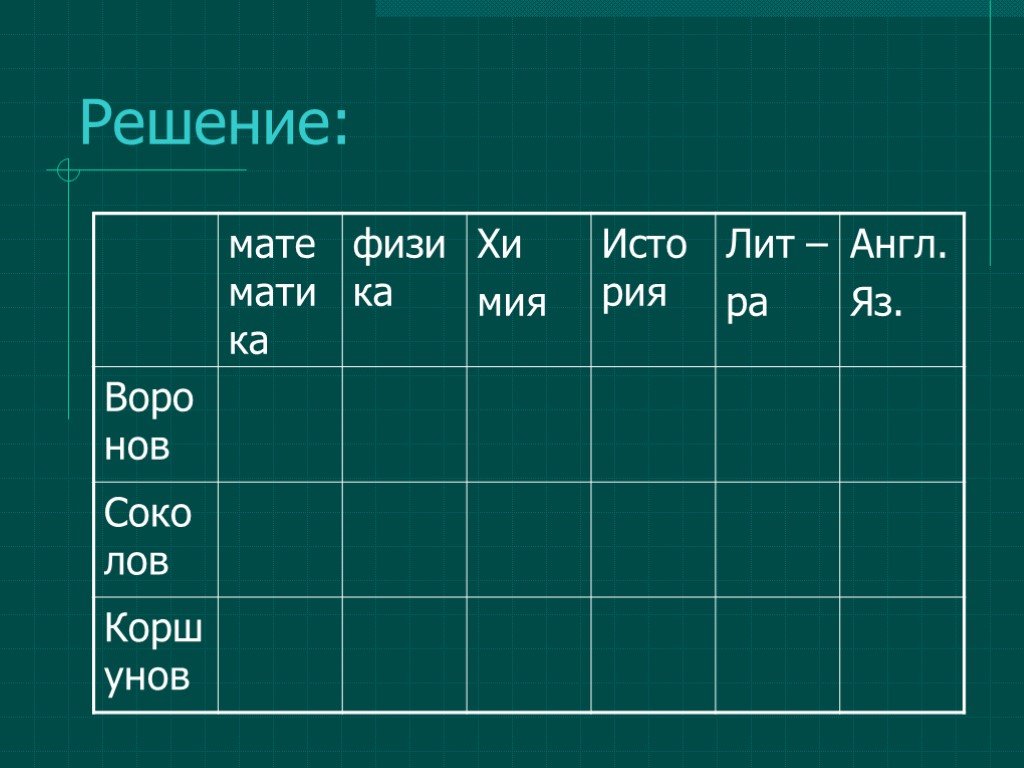
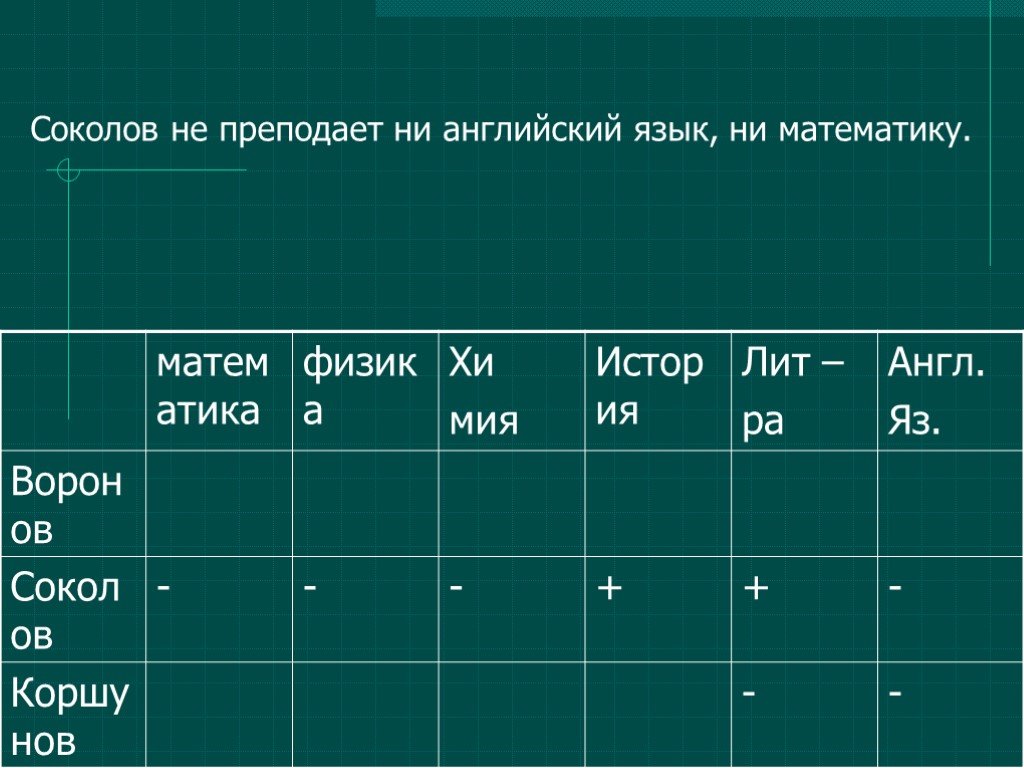
Введение. Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, ...Логические задачи
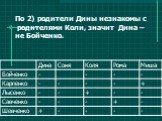
Пётр - сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору? задача 1 внуком сыном дедом. 2 4 6. Уменьшаемое больше вычитаемого на 2. Чему ...Логические задачи на переправу без чисел
Цель: собрать материал о логических играх без чисел, систематизировать и представить материал для работы в школьных математических кружках. Задачи. ...Занимательные логические задачи
1. Судаки. Полтора окуня стоят полтора рубля. Сколько рублей стоят 9 окуней? 9. 2. Яблоки. Как разделить пять яблок между пятью девочками так, чтобы ...Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). ...Великие задачи математики. Квадратура круга
Автор: Монахов Станислав. МОУ "Средняя общеобразовательная школа № 59". Курск - 2006. Меня зовут Монахов Станислав. Я ученик 6-го класса, очень люблю ...Введение понятия "Задачи. Составные части задачи
4. 10. . . 3. Проверьте! 4 10 5 6 3 3 4 5 6 10. Что отсутствует у нашего солнышка, а в математике учит считать? Учит луч! 1 2 5 6 7 8 9 0+1 1+1 2+1 ...Комбинаторные задачи
Что такое комбинаторика? В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа ...Комбинаторные задачи и их решения
1) Цели и задачи 2) Пояснительная записка 3) Требования к уровню подготовки 4) Учебно– тематический план 5) Содержание программы 6) Поурочное планирование ...Основные задачи на проценты
Как найти 1% от числа? 1% это одна сотая часть, надо число разделить на 100. Деление на 100 можно заменить умножением на 0,01. Поэтому, чтобы найти ...Подобные треугольники, решаем задачи по геометрии
8 9 10 11 14 15 16 17 18 30 1 3 4 5 6 13 19 7. Найти: Дано: А B D С 20. 2. 21. . . C M K N. . O. B1 А1 А2 А3 А4 B2 B3 B4. . . . 12. . P Подсказка. ...геометрия решение задачи
Дано: а-прямая, A B а Построить: BC=2AB Решение:. A,B-точки на прямой,. (на луче BA). Измерим циркулем расстояние между A и B,. отложим отрезок AC ...Графический метод и симплекс-метод задачи линейного программирования
Графический метод решения ЗЛП. Графический метод основан на геометрической интерпретации задачи линейного программирования. Найти минимальное решение ...Геометрические задачи со спичками
1. Уберите 4 спички так, чтобы осталось 4 маленьких и 1 большой квадраты. Ответ :. 2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, ...Геометрические задачи типа «С4»
Задачи Желаю успеха! "Дорогу осилит идущий!". Помните:. В треугольнике АВС АВ=15, ВС = 12, СА = 9. Точка D лежит на прямой ВС так, что BD:DC = 3:8. ...Геометрические задачи с практическим содержанием
введение. Решение геометрических задач с практическим содержанием позволяет: усилить практическую направленность изучения школьного курса геометрии; ...Геометрические задачи на экстремум
Определения. Задачи, где требуется определить условия, при которых некоторая величина принимает наибольшее и наименьшее значение, принято называть ...Конспекты
Простые арифметические задачи на определение продолжительности, начала и конца события 7 класс
Простые арифметические задачи на определение продолжительности, начала и конца события. 7 класс. Цели урока:. - Формировать умения решать текстовые ...Простые арифметические задачи на разностное сравнение
Конспект открытого урока по математике в 5 классе 8 вида. Тема урока. : «Простые арифметические задачи на разностное сравнение». Тип урока. ...Упражнения и задачи на усвоение таблицы деления на 2. Закрепление
Урок математики во 2 классе. Тема: Упражнения и задачи на усвоение таблицы деления на 2. Закрепление . . Урок - закрепление. Цели:. -Воспроизводить ...Взаимно обратные задачи
Математика. Тема:. Взаимно обратные задачи. Цель:. Сформировать представление о взаимно обратных задачах, умение их распознавать и составлять задачи ...Решение задач. Обратные задачи
. . Урок математики 2 класса. Тема урока: Решение задач. Обратные задачи. Цель: . закрепить навык решения изученных задач. Задачи:. ...Составление краткой записи условия задачи
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №2. им. А. А. Араканцева г. Семикаракорска». Конспект ...Задача. Структура задачи
Технологическая карта урока математики в 1 классе. . МБОУ СОШ №174. Учитель:. Павлова Елена Валерьевна. Дата проведения:. 18 марта 2014г. ...Решаем задачи
Конспект урока математики в 1 классе с учетом ФГОС. Составлен учителем высшей категории МАОУ гимназия №16 Козловой М.А. Тема урока: «. Решаем ...Девять решений геометрической задачи
Муниципальное бюджетное общеобразовательное учреждение. «Верхнеуслонская средняя общеобразовательная школа». Верхнеуслонского муниципального района ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:29 слайд(ов)
Поделись с друзьями:
Скачать презентацию