Презентация "Правильные многогранники" по математике – проект, доклад
Презентацию на тему "Правильные многогранники" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 10 слайд(ов).
Слайды презентации
Список похожих презентаций
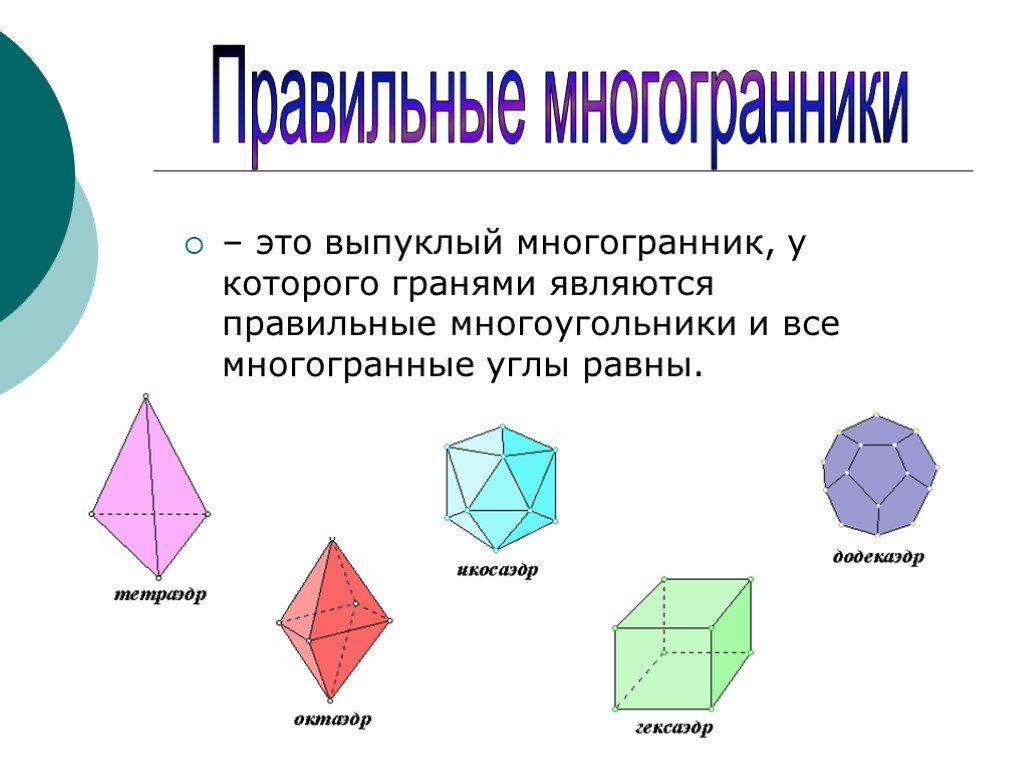
Правильные многогранники
Определение:. Правильный многогранник или платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий ...Правильные многогранники
Что такое правильный многогранник? Правильный многогранник - многогранник, все грани которого - одинаковые правильные многоугольники и все многогранные ...Правильные многогранники
Определение:. правильный многогранник - такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные ...Симметрия в пространстве. Правильные многогранники
СИММЕТРИЯ В ПРОСТРАНСТВЕ. «Симметрия … есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман ...Правильные многогранники
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. ...Правильные многогранники
Правильный многогранник или платоново тело — это выпуклый многогранник с равными гранями, которые составляют правильные многоугольники. Существует ...Правильные многогранники
СИММЕТРИЯ В ПРОСТРАНСТВЕ. “Симметрия является той идеей, посредством которой человек пытался постичь и создать порядок, красоту и совершенство” (Г.Вейль). ...Правильные многогранники
Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1. Точка О считается симметричной самой себе. Симметрия ...Правильные многогранники
Геометрический кроссворд. Какое тело носит имя Хеопса? Что представляет собой боковая грань пирамиды? Как называется правильный четырехугольник? Наука ...Правильные многогранники в геометрии
Цели: Знакомить учащихся с новым типом многогранников - правильными многогранниками. Показать влияние правильных многогранников на возникновение филосовских ...Правильные многогранники
Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников. Грани многогранника - это многоугольники, которые ...Правильные многогранники в четырехмерном пространстве
Абстрактный Тороидальный Гексадекаэдр — это комбинаторно-топологический объект — правильная триангуляция тора с 8 вершинами и 16 гранями. С. А. Л., ...Правильные многогранники в жизни
Цели:. Изучить виды, свойства правильных многогранников Рассмотреть использование геометрических тел в архитектуре Изучить один из видов искусства ...Правильные многогранники и их построение
Цели и задачи:. Дать понятие правильных многогранников ( на основе определения многогранников). Доказать почему существует только 5 типов правильных ...Правильные многогранники и их приметы
Многогранник называется правильным если:. 1) ОН ВЫПУКЛЫЙ. (Т.Е. ЛЕЖИТ ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ ГРАНИ). 2) ВСЕ ЕГО ГРАНИ – РАВНЫЕ ПРАВИЛЬНЫЕ ...Правильные многогранники и их развертки
Цели урока:. Познакомить учащихся с правильными многогранниками и их развертками, показать их в объеме и в движении, а также показать возможности ...Правильные многогранники
Определение правильного многогранника. Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и ...Правильные многогранники
Первым свойства правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные многогранники называют также телами Платона. ...Правильные и полуправильные многогранники
Учение о правильных многогранниках изложил в своих трудах Платон. С тех пор правильные многогранники называют Платоновыми телами. Существует пять ...Платоновы тела Правильные выпуклые многогранники
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл. ...Конспекты
Правильные многогранники
Урок геометрии в 11 классе. «Правильные многогранники». Учитель математики КГУ «Гимназия №6 г. Семей» Бочарова Галина Борисовна. Цель: Знакомство ...Правильные многогранники
Урок по теме: «Правильные многогранники». Тип урока:. изучение нового материала. Продолжительность урока. : 2 урока по 45 минут. Цель урока:. ...Правильные многогранники
2. . . Конспект урока геометрии с применением ИКТ в 10 классе. Тема:. Правильные многогран. ники. Цели урока:. Предметный компонент:. Изучение ...Правильные многогранники
Муниципальное общеобразовательное учреждение. . средняя общеобразовательная школа №5. Урок геометрии в 11 классе. «Правильные многогранники». ...Правильные многогранники
Тема урока: "Правильные многогранники". (10 класс). Учитель математики Иманова Алена Викторовна. МБОУ «Средняя общеобразовательная школа №21». ...Правильные многогранники. Тела Архимеда. Тела Кеплера-Пуансо
. . . . . . дисциплина. : геометрия. План урока. № 13-14. Тема урока:. Правильные многогранники. Тела Архимеда. Тела Кеплера-Пуансо. ...Обыкновенные дроби. Правильные и неправильные дроби
Методическая разработка урока проверки знаний. Урок математики в 5-м классе. Повторение по теме "Обыкновенные дроби. Правильные и неправильные дроби". ...Правильные многоугольники
ФИО автора материала: Мосолкова Людмила Васильевна. . Место работы (название образовательного учреждения: МБОУ г. Магадана «СОШ с УИМ № 15». . ...Правильные и неправильные дроби
План-конспект урока. . Учителя. математики и информатики. . МБОУ СОШ. №20. ФИО. Лютова Ирины Сергеевны. . Класс: 5. Предмет: математика. ...Правильные и неправильные дроби
Солдатова. . Ирина Валерьевна. I. квалификационная категория. Самарская область Исаклинский район с. Исаклы. ГБОУ СОШ с. Исаклы. Математика. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 сентября 2019
Категория:Математика
Содержит:10 слайд(ов)
Поделись с друзьями:
Скачать презентацию