Презентация "Логические задачи и загадки" по математике – проект, доклад

"Логические задачи и загадки"

Исследовательская работа:

Выполнили: учащиеся 6 класса МОУ «Ярабайкасинская СОШ» Моргаушского района ЧР Андреева Ксения Емельянова Наталия Петрова Екатерина Руководитель: Ярусова Альбина Петровна

Введение

Увлечение математикой часто начинается с размышлений над какой-то особенно понравившейся задачей. Она может встретиться и на школьном уроке, и на занятии математического кружка, и в журнале или книжке. А нас очень заинтересовали логические задачи, с которыми мы столкнулись на уроке информатики и математики. И мы решили узнать о них больше.

Цель:

Привитие интереса учащихся к логическим задачам и развитие их математического мышления.

Задачи:

Узнать, какие бывают логические задачи? Узнать историю происхождения загадки? Какова роль логических задач? Разобрать задачи, которые нам особенно понравились. Заинтересовать остальных темой нашей исследовательской работы. Проверить уровень логического мышления учащихся 6 класса.

История происхождения загадки

ЗАГАДКА - это мудреный вопрос. Основное назначение загадки в том, что она развивает в человеке догадливость, сообразительность. Избушка нова, а жильца нет. Жилец появится, изба развалится. Первобытный человек, прибегавший к особой иносказательной форме речи, был убежден, что скрывает приготовления к охоте, не называя своих орудий, зверей, намерений. Прибегая к иносказанию, он не дает возможности зверям узнать об опасности и тем самым обеспечивает себе удачный промысел. Бьют меня палками, Жмут меня камнями, Держат меня в огненной пещере, Режут меня ножами. За что меня так губят? За то, что любят.

По убеждению первобытного охотника, скотовода, пахаря в поле, в лесу, на воде, в жилище - везде и всюду человек постоянно сталкивается с враждебной сознательной силой, насылающей неудачу - пожар, болезнь. Эту силу необходимо перехитрить, а для этого необходима тайная условная речь. Без знания этой условной речи юноша не мог стать равноправным членом своего родного коллектива. Наряду с прочими для юношей устраивались испытания в его мудрости. Из липы свито дырявое корыто, По дороге идем - клетки кладем.

Позже крестьянские обычаи предписывали загадывать загадки в определенное время и при определенных обстоятельствах. В народных свадебных обычаях вплоть до XIX века загадывание загадок составляло обязательную принадлежность свадебного обряда. Владимир Даль записал пословицу, которую приводили в назидание жениху: "Выбирай такого дружку, чтоб загадки разгадывал". В сказках царевна выходит замуж за того, кто сумел отгадать ее загадки. Запрещалось загадывать загадки не вовремя-летом и днем. Это вызывало напасти. У древних греков и германцев, как говорят предания, загадывание загадок приравнивалось к единоборству. Согласно легендам и преданиям, не отгадавший загадки расплачивался жизнью. Пришли гости - и под лавку

Загадывание загадок русалками и тому подобными сверхъестественными существами воспроизводит в мифологических образах познание и борьбу человека с силами природы. Человек стремился разгадать тайный язык природы, чтобы овладеть ею. Вот, оказывается, какая интересная история у загадки - окунитесь с головой в этот мир - и он не даст вам скучать.

Логические задачи и загадки

Загадки Старинные задачи Задачи со спичками Логика и рассуждения Со словами Криптарифмы Взвешивание Последовательности О времени Бред профессора

Загадки

Загадка - это вопрос, в котором скрывается под «маской» определенное слово, а на предмет загадывания делается только лишь намек. Логические загадки развивают в человеке догадливость, сообразительность и интеллект. Решение загадок всегда пойдет на пользу.

Загадка 1 Накормишь – живет, Напоишь – умрет. Ответ Загадка 2 Вам дали это, это и сейчас принадлежит вам. Вы его никогда никому не передавали, но им пользуются все ваши знакомые. Что это? Ответ Загадка 3 Моя жизнь может быть измерена в часах. Я служу, когда пожираюсь. Когда я тонка, я быстра. Когда я толста, я медленна. Ветер мой враг Кто я? Ответ Загадка 4 В тихую погоду - нет нас нигде, А ветер подует - бежим по воде. Ответ Загадка 5 Мальчик рассказал своей учительнице, что отсутствовал вчера в школе из-за день рождения своих родных отца и деда. Оба вместе отмечают свои день рождения и, кроме того, оба родились в один день и в один год. Возможно ли такое, или мальчик просто прогулял школу и придумал неудачную отговорку? Ответ

Старинные задачи

Старинные задачи предоставляют замечательную возможность проследить за развитием математической мысли с древнейших времён. Наиболее древние письменные математические тексты датируются примерно началом II тыс. до н.э. Математические документы сохранились только в Египте, Вавилоне, Китае и Индии.

Задача «Суд Париса»

Богини Гера, Афродита и Афина пришли к юному Парису, чтобы тот решил, кто из них прекраснее. Представ перед Парисом, богини высказали следующие утверждения. Афродита. Я самая прекрасная. (1) Афина. Афродита не самая прекрасная. (2) Гера. Я самая прекрасная. (3) Афродита. Гера не самая прекрасная. (4) Афина. Я самая прекрасная. (5) Парис, прилёгший отдохнуть на обочине дороги, не счёл нужным даже снять платок, которым прикрыл глаза от яркого солнца. Но богини были настойчивы, и ему нужно было решить, кто из них самая прекрасная. Парис предположил, что все отверждения прекраснейшей из богинь истинны, а все утверждения двух остальных богинь ложны. Мог ли Парис вынести решение, кто прекраснее из богинь? Ответ

Задачи со спичками

Задачи, в которых совершая манипуляции над спичками, необходимо добиться требуемого результата. Помогает развивать сообразительность, находчивость, догадливость и умение рассуждать. Задача 1. Задача 2. Задача 3. Задача 4. Задача 5.

Логика и рассуждения

Задача 1. Утверждения Задача 2. Стоимость книги. Задача 3. Волшебная фраза Задача 4. Цвет волос художника Задача 5. Четыре друга

Логика

Задача 1. Утверждения

Определите, какие из следующих утверждений являются истинными и какие ложными. 1. Одно утверждение в этом списке ложно. 2. Две утверждения в этом списке ложны. 3. Три утверждения в этом списке ложны. 4. Четыре утверждения в этом списке ложны. 5. Пять утверждений в этом списке ложны. 6. Шесть утверждении в этом списке ложны. 7. Семь утверждений в этом списке ложны. 8. Восемь утверждений в этом списке ложны. 9. Девять утверждений в этом списке ложны. 10. Десять утверждений в этом списке ложны.

Ответ

Ответ задачи 1. Утверждения

Все утверждения ложны, кроме девятого.

Задача 2. Стоимость книги

За книгу заплатили 100 руб. и осталось заплатить еще столько. Сколько осталось бы заплатить, если бы за нее заплатили бы столько, сколько осталось заплатить? Сколько стоит книга ?

Ответ задачи 2. Стоимость книги

Еще столько же, всего - 200 руб.

Задача 3. Волшебная фраза

Один путешественник был захвачен племенем, вождь которого решил, что тот должен умереть. Вождь был очень мудрым человеком и дал путешественнику право выбора. Путешественник должен был сказать одну фразу. Если фраза оказывалась правдивой, то его сбрасывали с высокой скалы. Если она была лживой, то путешественника должны были растерзать львы. Но путешественник сказал такую фразу, после которой его отпустили. Какую?

Ответ задачи 3. Волшебная фраза

Он сказал: "Меня растерзают львы". Теперь, если бы вождь отдал его на растерзание львам, то эта фраза оказалась бы правдивой, и путешественника должны были бы сбросить со скалы. Но если его сбросят со скалы, то фраза окажется лживой. Вождь признал, что единственно правильным решением будет отпустить путешественника.

Задача 4. Цвет волос художника

В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. "Замечательно, что у одного и нас белые, у другого чёрные, а у третьего рыжие волосы, но ни у кого цвет волос не соответствует фамилии", - заметил черноволосый. "Ты прав", - сказал Белов. Какой цвет волос у художника?

Ответ задачи 4. Цвет волос художника

У художника чёрный цвет волос

Задача 5. Четыре друга

Жили четыре друга. Звали их Альберт, Карл, Дитрих и Фридрих. Фамилии друзей те же, что и имена, только так, что ни у кого из них имя и фамилия не были одинаковыми, кроме того, фамилия Дитриха не Альберт. Определите фамилию и имя каждого мальчика, если известно, что имя мальчика, у которого фамилия Фридрих, есть фамилия того мальчика, имя которого - фамилия Карла.

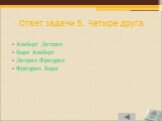
Ответ задачи 5. Четыре друга

Альберт Дитрих Карл Альберт Дитрих Фридрих Фридрих Карл

Со словами

Наличие этого раздела не означает, что в остальных - задачи без слов. В этом разделе собраны филологические загадки, где нужно вычислить логику слов, подобрать подходящее к последовательности или разгадать словесный каламбур. Задача 1. Спорт Задача 2. Известная латынь Задача 3. Фраза Задача 4. Из мухи слона Задача 5. Самое маленькое животное

Криптарифмы

Криптарифм (cryptarithm) - это математический ребус, в котором зашифрован пример на выполнение одного из арифметических действий. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Считается, что никакое число не должно начинаться с нуля. Криптарифм можно считать хорошим, если в результате шифрования получилась какая-то осмысленная фраза. Например, классическим криптарифмом является пример на сложение, придуманный Генри Э. Дьюдени еще в начале нашего века: SEND+MORE=MONEY. Кроме того, еще одно требование к правильному криптарифму: он должен иметь единственную возможную расшифровку. Например, единственным решением криптарифма Дьюдени является 9567+1085=10652. Задача 1. Нитки Задача 2. Пример Задача 3. Вагоны Задача 4. Наука Задача 5. ABCDE

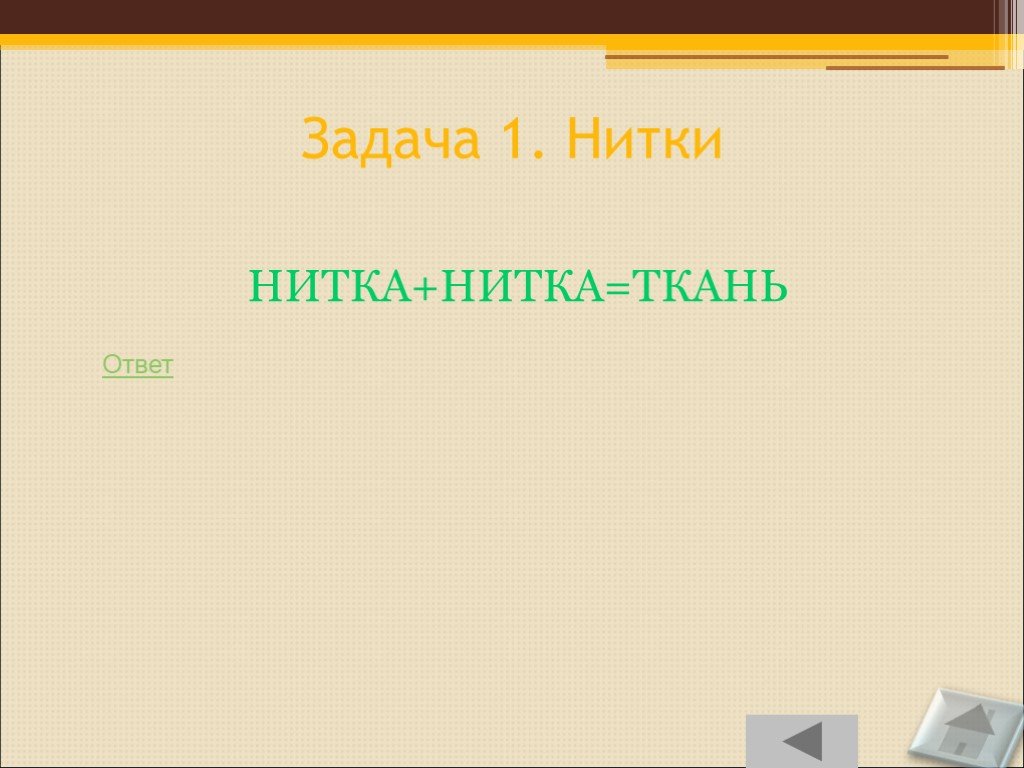
Задача 1. Нитки НИТКА+НИТКА=ТКАНЬ

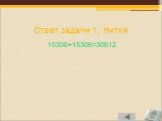
Ответ задачи 1. Нитки

15306+15306=30612

Задача 2. Пример

В этой задаче цифры заменены буквами. Одинаковыми буквами заменены одинаковые цифры. Восстановите зашифрованные цифры: ПРИМЕР РИМЕР ИМЕР МЕР ЕР Р ---------- ЗАДАЧА

Ответ задачи 2. Пример

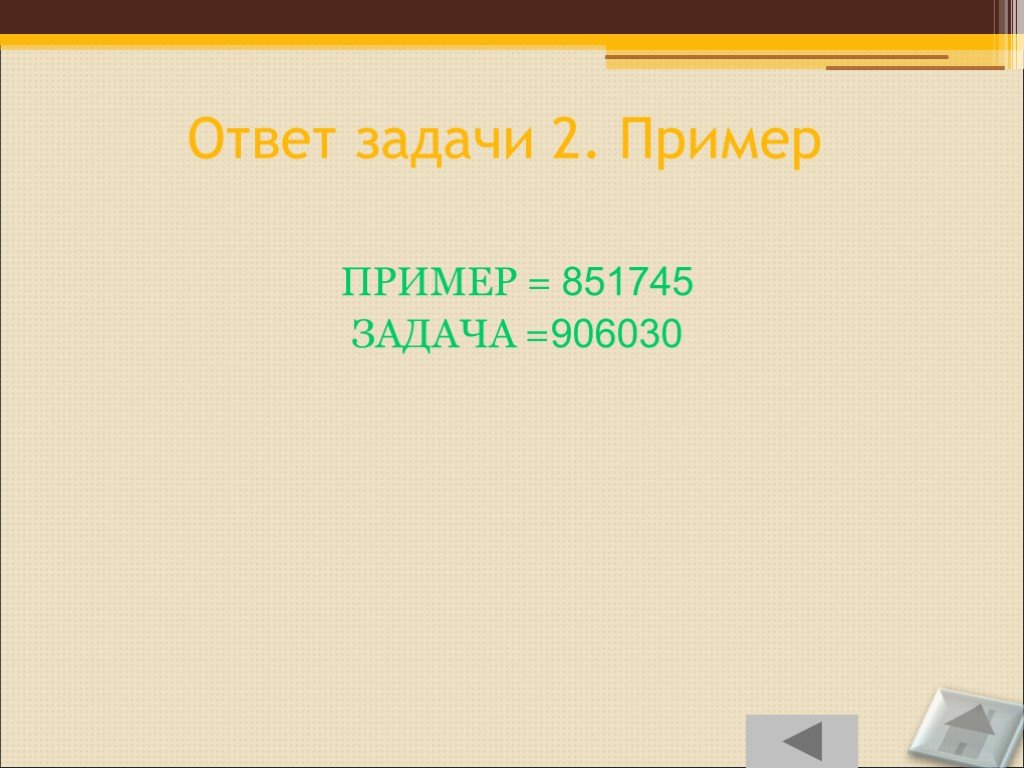
ПРИМЕР = 851745 ЗАДАЧА =906030

Задача 3. Вагоны

Замените буквы на цифры, чтобы добиться равенства: ВАГОН + ВАГОН = СОСТАВ

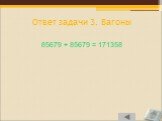
Ответ задачи 3. Вагоны

85679 + 85679 = 171358

Задача 4. Наука

КНИГА + КНИГА + КНИГА = НАУКА

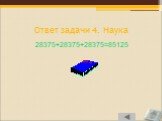
Ответ задачи 4. Наука

28375+28375+28375=85125

Задача 5. ABCDE

Замените буквы цифрами так, чтобы пример на умножение был верен. Каждой букве соответствует только одна цифра. Разным буквам не могут соответствовать одинаковые цифры. ABCDE * 4 ----------- EDCBA

Ответ задачи 5. ABCDE

21978 * 4 --------- 87912 Рассуждения такие: A A=2 => E=8 => B

Взвешивание и переливание

Задачи на взвешивание - распространённый вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. В задачах на переливание необходимо получить определенное количество жидкости, используя емкости заданного объема. Задача 1. Мешки с золотом. Задача 2. Набираем воду Задача 3. Квас на двоих Задача 4. Задача Пуассона Задача 5. Легче или тяжелее?

Задача 1. Мешки с золотом

Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном - все фальшинвые. Одна настоящая монета весит 5 грамм, а фальшивая - 4 грамма. Есть весы, показывающие вес в граммах. Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты?

Ответ задачи 1. Мешки с золотом

Пронумеруем мешки от 1 до 10. Вытащим из первого 1 монету, из второго 2, из третьего 3 и так далее. Затем возьмем всю эту кучу монет и положим на весы. Если бы они все были настоящие, то общий вес составил бы 275 грамм (т.к. мы вытащили в общей сложности 55 монет). Но в одном из мешков были фальшивые. Если это был первый мешок, то вес будет на 1 грамм меньше (т.к. мы взяли оттуда 1 монету). Если фальшивые были во втором, то на 2 грамма меньше. И так далее.

Задача 2. Набираем воду

Как, имея пятилитровое ведро и девятилитровую банку, набрать из реки ровно три литра воды?

Ответ задачи 2. Набираем воду

Заполняем 9-литровую банку и заливаем из нее в 5-литровое ведро. (Далее 5-литровка и 9-литровка). В 9 -литровке 4 литра. выливаем воду из 5-литровки и заливаем туда 4 литра из 9-литровки. Заполняем 9-литровку и выливаем оттуда 1 литр в пятилитровую. Выливаем воду из 5-литровки, и заполняем 5-литровку из 9-литровки. Всё! В 9-литровке теперь 3 литра. Если 5 литров в ведре не нужно, их можно вылить.

Задача 3. Квас на двоих

Двое должны разделить поровну 8 вёдер кваса, находящегося в большом бочонке. Но у них есть ещё только два пустых бочонка, в один из которых входит 5 вёдер, а в другой - 3 ведра. Спрашивается, как они могут разделить этот квас, пользуясь только этими тремя бочонками? Решите задачу двумя способами.

Ответ задачи 3. Квас на двоих

решение 1 Большой 5-ведёрн. 3-ведёрн. До переливания 8 0 0 После 1-го переливания 3 5 0 После 2-го переливания 3 2 3 После 3-го переливания 6 2 0 После 4-го переливания 6 0 2 После 5-го переливания 1 5 2 После 6-го переливания 1 4 3 После 7-го переливания 4 4 0

решение 2 Большой 5-ведёрн. 3-ведёрн. До переливания 8 0 0 После 1-го переливания 5 0 3 После 2-го переливания 5 3 0 После 3-го переливания 2 3 3 После 4-го переливания 2 5 1 После 5-го переливания 7 0 1 После 6-го переливания 7 1 0 После 7-го переливания 4 1 3 После 8-го переливания 4 4 0

Задача 4. Задача Пуассона

Как из полного сосуда ёмкостью в 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью в 8 и 5 л.

Ответ задачи Пуассона

Сначала наливаете 8 литров в 8л., потом из 8л. наливаете полный 5л., в результате получается, что в 12л.-4 литра, в 8л-3литра, а в 5л.-5 литров. Переливаете из 5л. в 12л. всю воду (или что там за жидкость), а из 8л. переливаете все 3 литра в 5л. В результате 9 литров в 12л, 0 литров в 8л., и 3 литра в 5л. Переливаете из 12л. 8 литров в пустой 8л.,и в 12 л. остается 1 литр. Из 8л. доливаете в 5л., пока 5л. не станет полным, (в 5л. было 3л., след. долили мы еще 2литра из 8л.) Тогда в 8л. как раз остается 6л.

Задача 5. Легче или тяжелее?

Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.

Ответ задачи 5. Легче или тяжелее?

Взвешиваешь 50 и 50 монет: 1) Равенство: Беpем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там 1.1 Левая кучка тяжелее => фальшивая монета тяжелее 1.2 Левая кучка легче => фальшивая монета легче 2) Hеpавенство: Беpем более тяжелую кучку и разбиваем ее на две кучки по 25 монет. 2.1 Вес кучек одинаковый => фальшивая монета легче 2.2 Вес кучек неодинаковый => фальшивая монета тяжелее

Последовательности

В этих задачах необходимо разгадать принцип, по которому задается определенная последовательность, и продолжить ее. Часто бывает так, что последовательность можно продолжить разными способами, и под каждый из них подобрать закономерность, по которому она строилась. Это можно считать дополнительным заданием - найти как можно больше законов построения той или иной последовательности. Решение логических задач на последовательности помогает в поисках ответа выйти за рамки. Тот, кому это легко удается, найдет больше всего вариантов.

О времени

Логические задачи о времени - вычислить дату, используя подсказки, вспомнить закономерность работы часов или определить чей-то возраст лишь по намекам - вот суть задач о времени. Задача 1. Парадокс Льюиса Кэрролла Задача 2. Что это за день? Задача 3. Одновременный бой Задача 4. Песочные часы Задача 5. Дни рождения

Задача 1. Парадокс Льюиса Кэрролла

Какие часы точнее показывают время: те, которые отстают на минуту в сутки, или те, которые вовсе не идут?

Ответ задачи 1. Парадокс Льюиса Кэрролла

Кэрролл считал, что точными являются стоящие часы. Вот как он это обосновывал. Часы, отстающие на минуту в сутки, показывают точное время один раз в два года, в то время как стоящие часы показывают точное время два раза в сутки.

Задача 2. Что это за день?

Если этот день не идет вслед за понедельником и не перед четвергом, а завтра не воскресенье и вчера было не воскресенье, а послезавтра будет не суббота и позавчера была не среда, то что это за день?

Ответ задачи 2. Что это за день?

Воскресенье

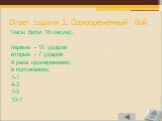
Задача 3. Одновременный бой

Двое часов начали и закончили бить одновременно. Первые бьют через каждые 2с, вторые - через каждые 3с. Всего было насчитано 13 ударов. Слившиеся удары воспринимаются как один. Сколько времени часы били?

Ответ задачи 3. Одновременный бой

Часы били 18 секунд. первые - 10 ударов вторые - 7 ударов 4 раза одновременно в положениях: 1-1 4-3 7-5 10-7

Задача 4. Песочные часы

Натали надо испечь яблочный пирог. Обычных часов у нее нет, но есть двое песочных часов. Одни - на 7 минут (No1), другие - на 11 минут (No2). Как ей точно вымерять 15 минут, необходимых для приготовления пирога?

Ответ задачи 4. Песочные часы

Она должна их перевернуть одновременно; когда в часах No1 песок пересыплется, она должна поставить пирог в печь; в часах No2 песок продолжает пересыпаться на протяжении 4-х минут; спустя 4 минуты Натали снова переворачивает часы No2 и ждет, пока весь песок не пересыплется.

Задача 5. Дни рождения

Мальчик говорит: позавчера мне еще было 10 лет, а в следующем году мне исполнится 13. Может ли такое быть?

Ответ задачи 5. Дни рождения

Может, если день рождения 31 декабря

Бред профессора

В этих головоломках все слова в крылатом высказывании (пословице или поговорке) заменены на наукообразные их определения. В результате и получился псевдонаучный бред... бред профессора. Например: Условием выживания биологической особи является ее перемещение по криволинейной замкнутой траектории. Ответ: Хочешь жить - умей вертеться. В общем, нужно отгадать пословицу, зашифрованную таким "научным" способом. Бред профессора 1. Бред профессора 2. Бред профессора 3. Бред профессора 4. Бред профессора 5.

Бред профессора 1.

Соответствие длительности процесса жизнедеятельности и процесса обучаемости человеческого индивидуума, означающее неизбежное завершение жизненного цикла в состоянии пониженного интеллектуального развития.

Ответ 1 бреда профессора

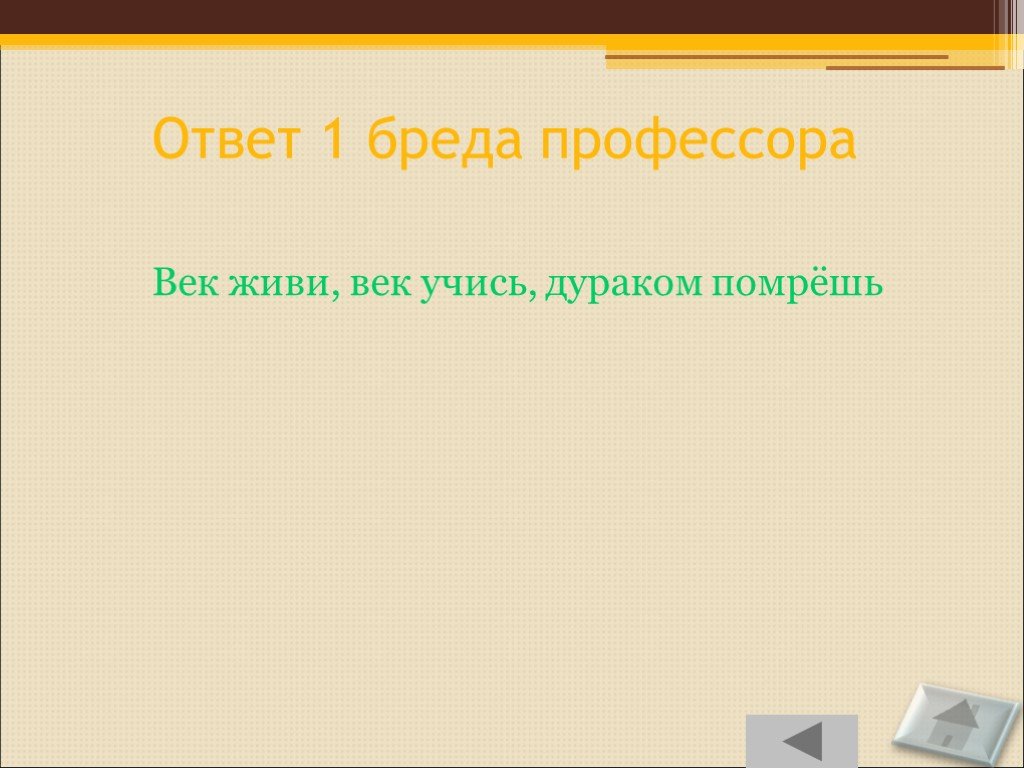
Век живи, век учись, дураком помрёшь

Бред профессора 2.

Способность живого организма переносить болевые ощущения и прочие раздражители в совокупности с процессом производства товаров и услуг позволяют привести окружающее пространство в порошкообразное состояние.

Ответ 2 бреда профессора

Терпение и труд всё перетрут

Бред профессора 3.

Непригодность к решению боевых задач воинских частей и соединений малой численности в условиях нахождения в открытом пространстве.

Ответ 3 бреда профессора

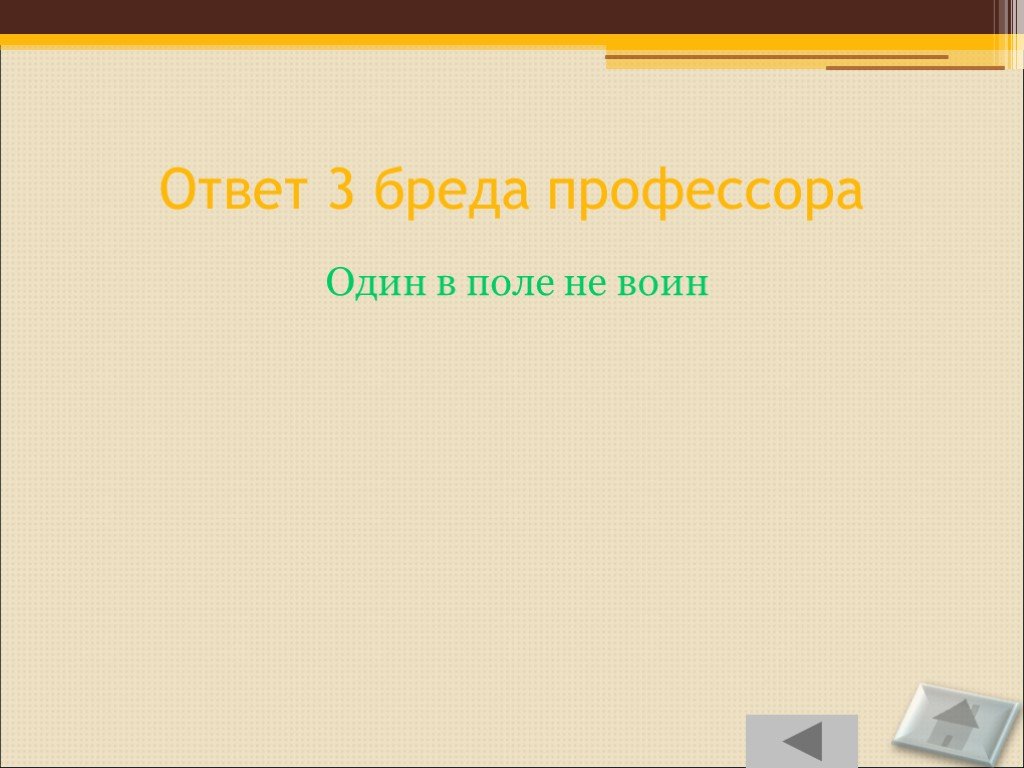
Один в поле не воин

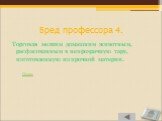
Бред профессора 4.

Торговля мелким домашним животным, расфасованным в непрозрачную тару, изготовленную из прочной материи.

Ответ 4 бреда профессора

Продать кота в мешке

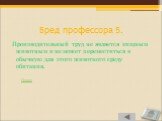
Бред профессора 5.

Производительный труд не является хищным животным и не может переместиться в обычную для этого животного среду обитания.

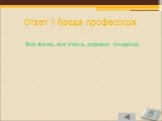
Ответ 5 бреда профессора

Работа не волк, в лес не убежит

Ответ загадки 1 Огонь

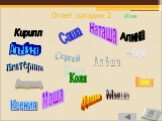
Ответ загадки 2 Имя Саша Маша Даша Коля Миша Ваня Сергей Алёша Кирилл Зоя Алина Альбина Ксения Наташа Екатерина Владимир

Ответ загадки 3 Свеча

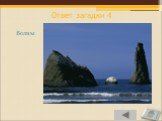
Ответ загадки 4 Волны

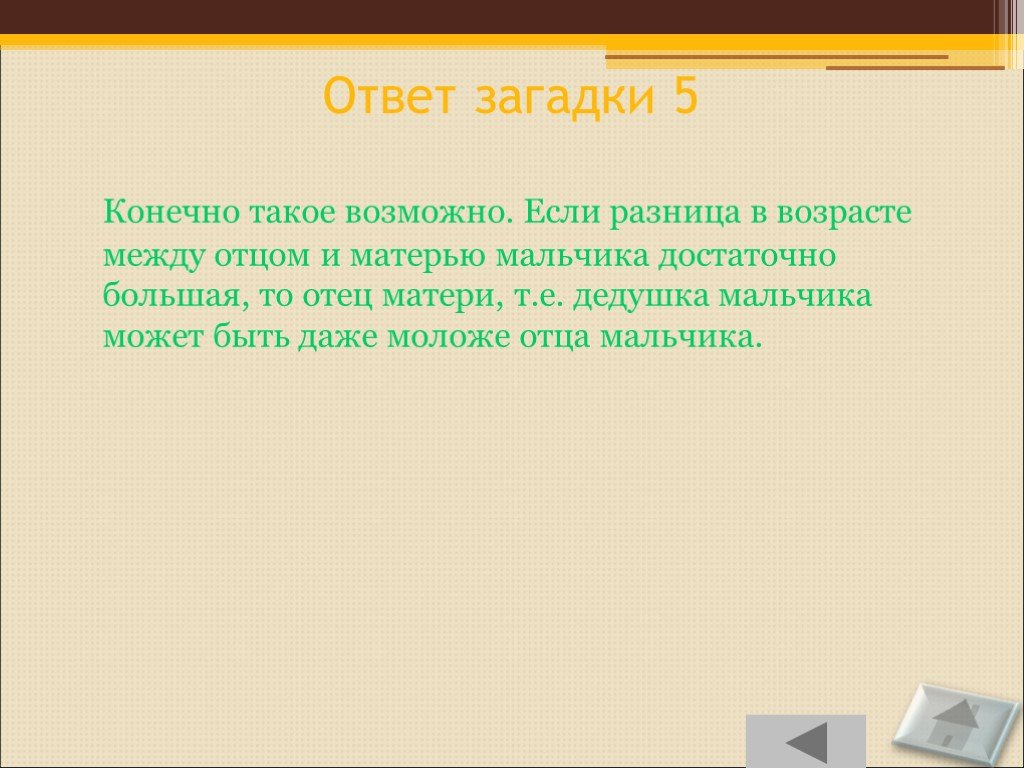
Ответ загадки 5

Конечно такое возможно. Если разница в возрасте между отцом и матерью мальчика достаточно большая, то отец матери, т.е. дедушка мальчика может быть даже моложе отца мальчика.

Из мухи слона

Вы думаете, невозможно сделать из мухи слона? Hепpавда! Можно, но трудно: МУХА - муpа - туpа - таpа - каpа - каpе - кафе - кафp - каюp - каюк - кpюк - уpюк - уpок - сpок - сток - стон - СЛОH. Муха пpевpатилась в слона всего лишь за 16 ходов. Как видите, пpи одном ходе можно заменять лишь одну букву, поpядок следования букв пpи этом менять нельзя. Попpобуйте по этим пpавилам совеpшить "путешествие во вpемени" - пpевpатить сначала МИГ в ЧАС, затем ЧАС в ГОД, затем ГОД в ВЕК, и наконец ВЕК в слово "ЭРА". Всего эта цепочка занимает 17 ходов. Получилось? Да или нет - ничего стpашного, но это еще не все. Попpобуйте тепеpь сделать "скачок во вpемени" - пpевpатить слово МИГ сpазу в слово ЭРА за 6 ходов. Ответ

Ответ задачи «Из мухи слона»

1) МИГ - маг - май - чай - ЧАС - чад - гад - ГОД - род - рок - бок - бек - ВЕК - бек - бок - боа - бра - ЭРА Или: ... - ГОД - гид - вид - вис - вес - ВЕК - ... Если использовать отсутствующее в словаре, но всем нам известное слово БОД (единица скорости передачи информации), то получается чуть короче: МИГ - маг - май - чай - ЧАС - чад - гад - ГОД - бод - бок - бек - ВЕК - бек - бок - боа - бра - ЭРА (слово БОД можно считать пpочно вошедшим в нашу жизнь неологизмом, а следовательно и использовать). 2) МИГ - мир - мор - бор - боа - бра - ЭРА

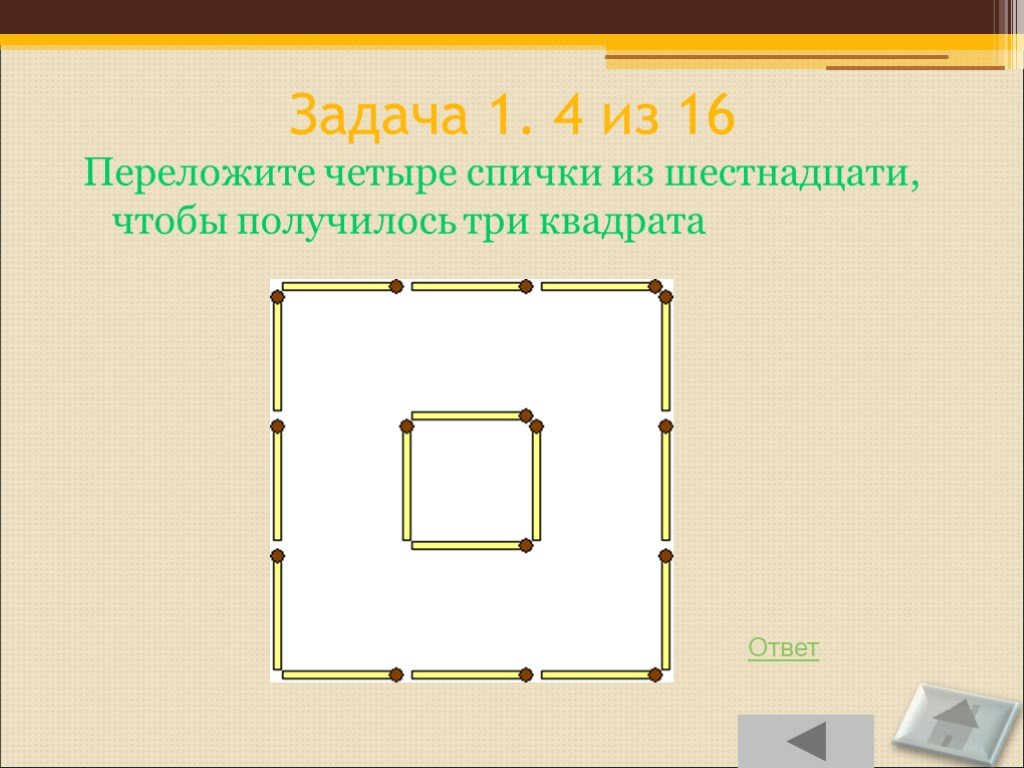
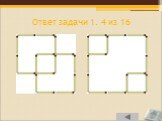
Задача 1. 4 из 16

Переложите четыре спички из шестнадцати, чтобы получилось три квадрата

Задача 2. Исправление на расстояние

Исправьте равенство так, чтобы оно стало верным, не дотрагиваясь, ни до одной спички (нельзя поджигать, перемещать, передвигать и т.д.).

Задача 3. Четыре квадрата

Переложите три спички из двенадцати так, чтобы получилось четыре одинаковых квадрата из трех.

Задача 4.

Добавьте нечетное количество спичек, разделив квадрат 4х4 (16 спичек) на четыре области по 4 клетки каждая. Гнуть, ломать и перекрещивать спички нельзя.

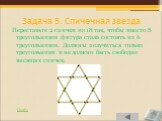
Задача 5. Спичечная звезда

Переставьте 2 спички из 18 так, чтобы вместо 8 треугольников фигура стала состоять из 6 треугольников. Должны получиться только треугольники и не должно быть свободно висящих спичек.

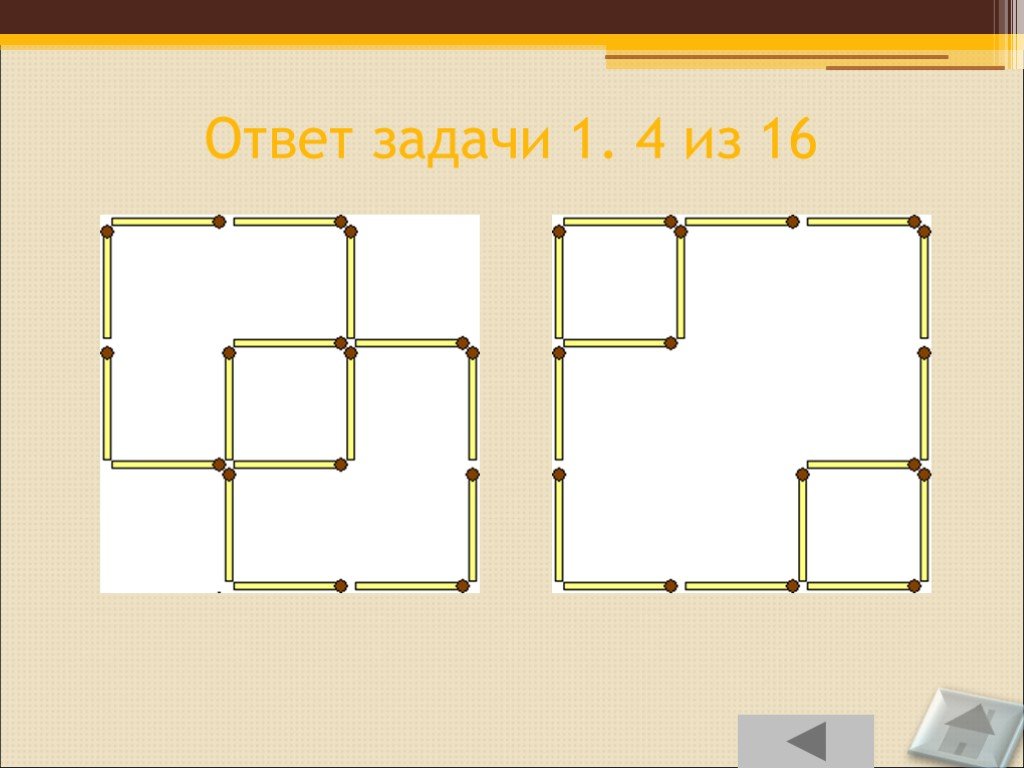
Ответ задачи 1. 4 из 16

Ответ задачи 2. Исправление на расстоянии

Достаточно перевернуть рисунок на 180 градусов

Ответ задачи 3. Четыре квадрата

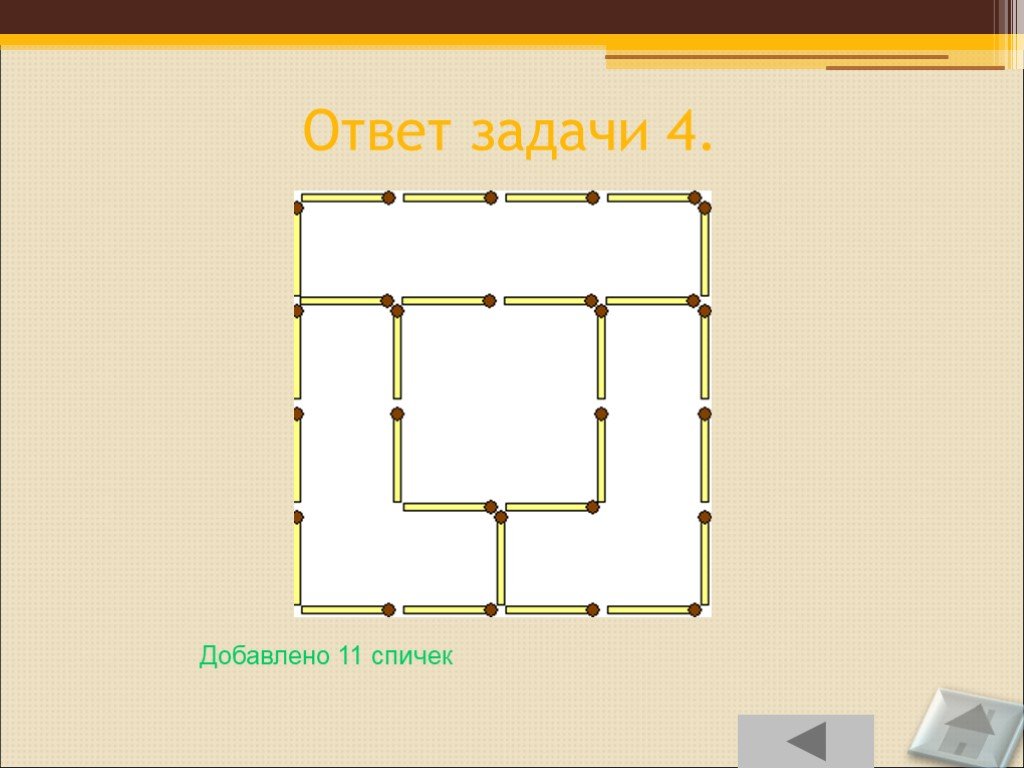
Ответ задачи 4.

Добавлено 11 спичек

Ответ задачи 5. Спичечная звезда.

Ответ задачи «Суд Париса»

Пусть Парис предположил, что Афина изрекла истину. Тогда она прекраснейшая из богинь, и по предположению утверждение (4) ложно. Мы приходим к противоречию, так как Гера не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь Афина. Таким образом, исходное предположение ложно. Если предположит, что истину изрекла Гера, то она прекраснейшая из богинь, и по предположению утверждение (2) ложно. Мы снова приходим к противоречию, так как Афродита не может быть прекраснейшей из богинь, коль скоро прекраснейшая из богинь. Отрицания утверждений (2), (3) и (5) истинны и показывают, что Афродита – прекраснейшая из богинь. Итак, по «суду Париса» прекраснейшей из богинь является Афродита.

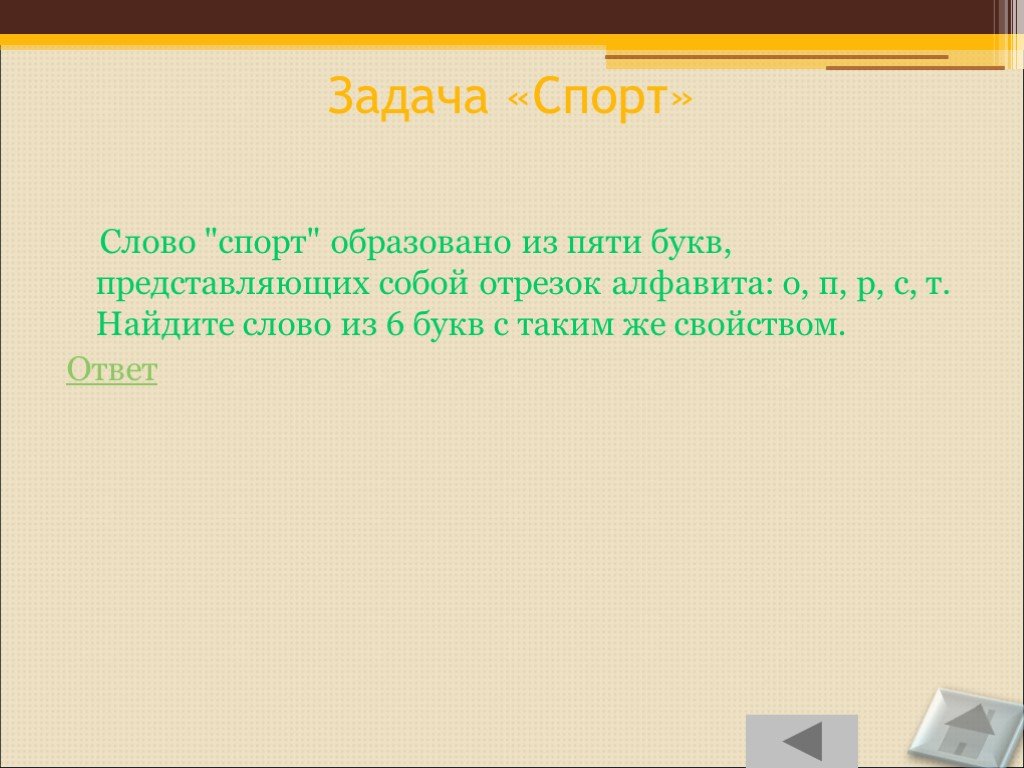
Задача «Спорт»

Слово "спорт" образовано из пяти букв, представляющих собой отрезок алфавита: о, п, р, с, т. Найдите слово из 6 букв с таким же свойством. Ответ

Ответ задачи «Спорт»

Слово "ступор" содержит 6 букв, которые образуют отрезок алфавита.

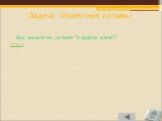
Задача «Известная латынь»

Как сказать по латыни "в другом месте"? Ответ

Ответ задачи «Известная латынь»

Алиби

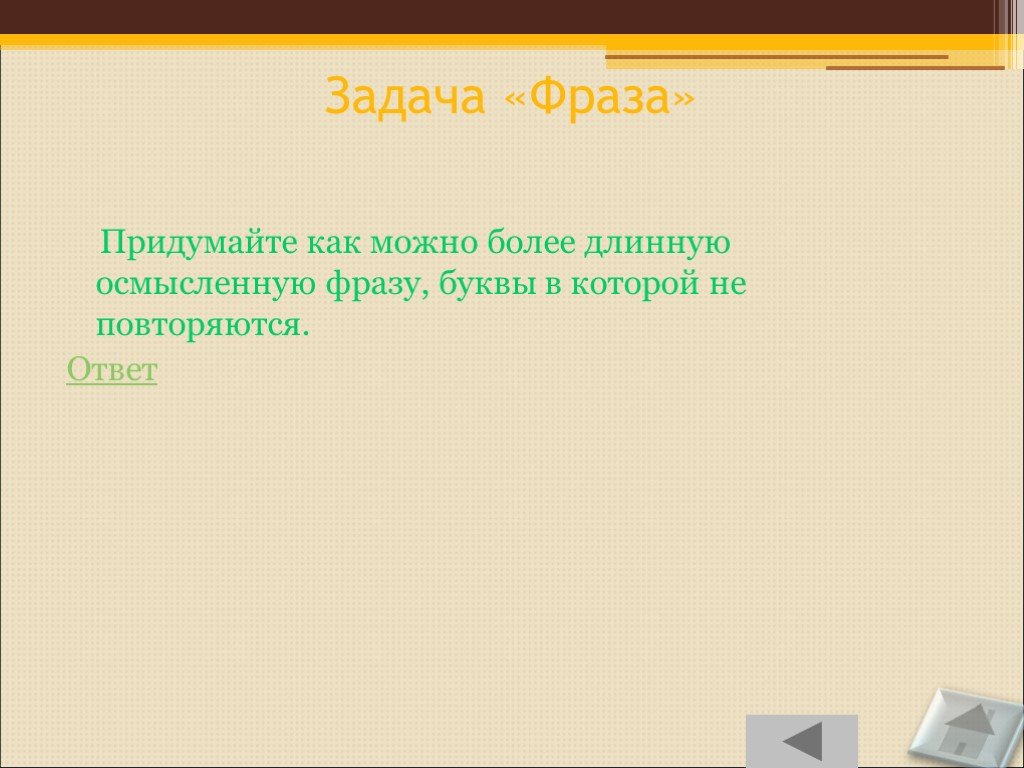
Задача «Фраза»

Придумайте как можно более длинную осмысленную фразу, буквы в которой не повторяются. Ответ

Ответ задачи «Фраза»

Наиболее длинная из известных фраз: "Эй, ёж, прячь своих мышек за дуб!" (задействованы 24 буквы из 33).

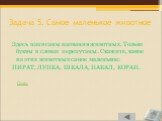
Задача 5. Самое маленькое животное

Здесь написаны названия животных. Только буквы в словах перепутаны. Скажите, какое из этих животных самое маленькое: ПИРАТ, ЛУНКА, ШКАЛА, НАКАЛ, КОРАН.

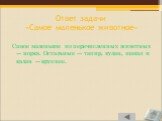
Ответ задачи «Самое маленькое животное»

Самое маленькое из перечисленных животных — норка. Остальные — тапир, кулан, шакал и калан — крупнее.

Выводы

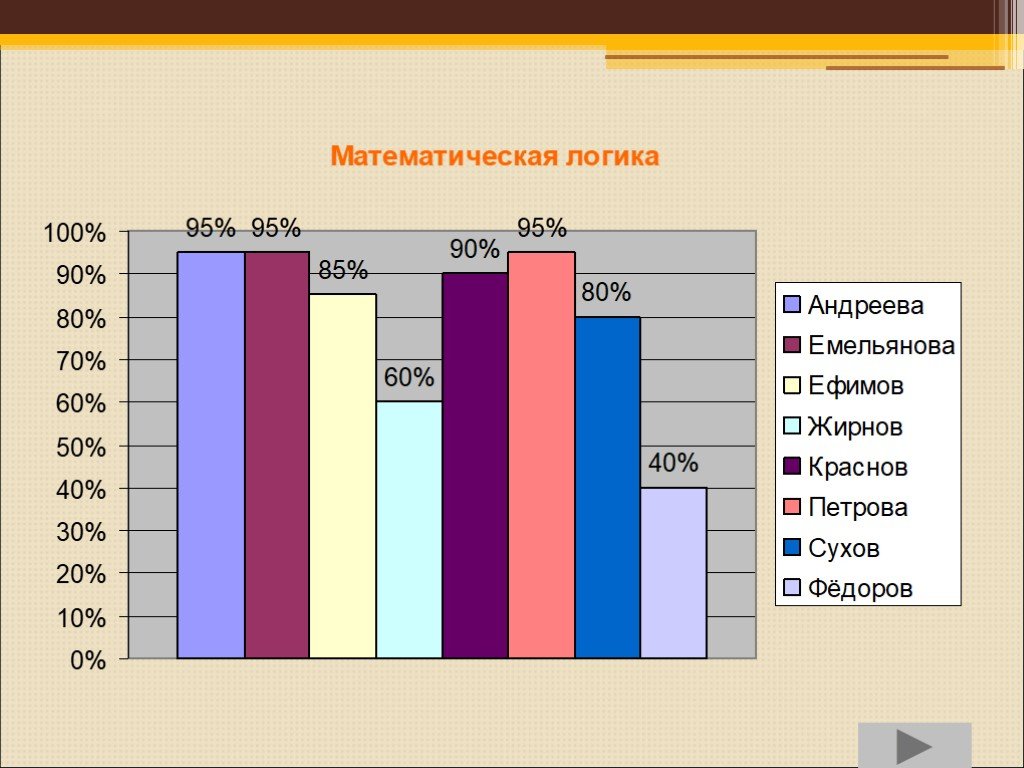
Практикой доказано, что ребята, имеющие хорошие математические навыки, математическую логику, математический и языковый интеллект успешны и по другим предметам. Мы в этом убедились сами. И достоверно доказано, что старение мозга человека происходит медленнее, если он занимается умственным трудом. Надеемся, что эта работа будет увлекательной и полезной не только для учащихся, но и для тех, кто уже давно перешагнул этот порог.

Список литературы и web-ресурсов

Баврин И.И., Фрибис Е.А. Старинные задачи: Кн. Для учащихся. – М.: Просвещение, 1994.- 128 с.: ил. – ISBN 5-09-005128-3. Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971. – 510 с. Климченко Д.В. Задачи по математике для любознательных. Чебоксары: Чувашгосиздат, 1963. – 43 с. Лебедева И.В. Занимательные игры для детей. – Москва: ИКЦ «МарТ»; Ростов н/Д: Издательский центр «МарТ», 2004. – 128 с. Мерлин А.В., Мерлина Н.И. Задачи для внеклассной работы по математике (5-11 классы): Учебное пособие. 2-е изд., испр. И доп. Чебоксары: Изд-во Чуваш. Ун-та, 2002. 218 с. 365 задач на смекалку. – М.: АСТ-ПРЕСС КНИГА. -272 С. – (Умникам и умницам) http://golovolomka.hobby.ru/ http://golovolomka.narod.ru/ http://www.origami.ru/ http://www.izvilina.com/pd.html http://igrushka.forever.kz/vip13/verput.html http://nazva.net/