Презентация "Решение тригонометрических уравнений" (10 класс) по математике – проект, доклад
Презентацию на тему "Решение тригонометрических уравнений" (10 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 28 слайд(ов).
Слайды презентации
Список похожих презентаций
Методы решения тригонометрических уравнений
Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. ...Ох уж эти показательные… Решение показательных уравнений и неравенств
Ответьте на вопросы. 1. Какая функция называется показательной? 2. Какова область определения показательной функции? 3. Какова область значений показательной ...Методы решения тригонометрических уравнений
«Думай о смысле, а слова придут сами». Льюис Кэрролл. Методы решения тригонометрических уравнений Указать метод решения уравнения:. . . . . . Методы ...Методы решения тригонометрических уравнений
ЦЕЛЬ:.Систематизировать, обобщить, расширить знания и умения, связанные с применением методов решения тригонометрических уравнений. . . 1. Какие ...
Методы решения тригонометрических уравнений
«Счастливый случай». 1 гейм «Разминка». 1. Решение уравнения вида cos x=a при |a| > 1? 2. При каком значении а, уравнение cos x =a имеет решения? ...Методы решения тригонометрических уравнений
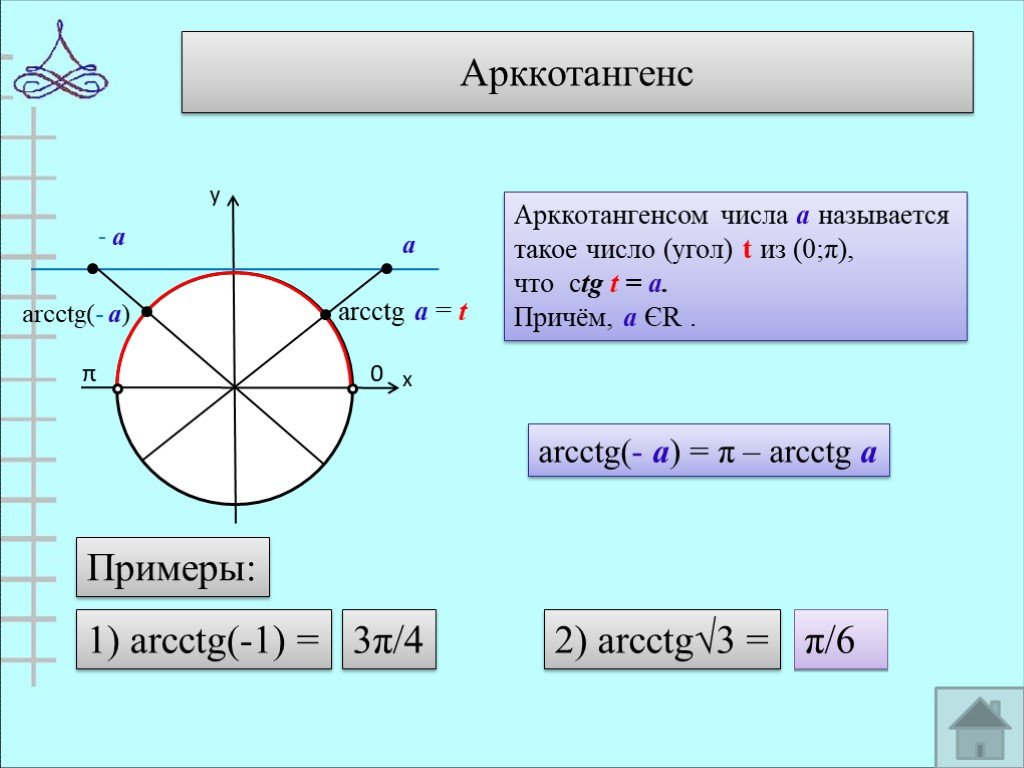
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Я. А. Коменский. Арксинус. ...Примеры решения тригонометрических уравнений
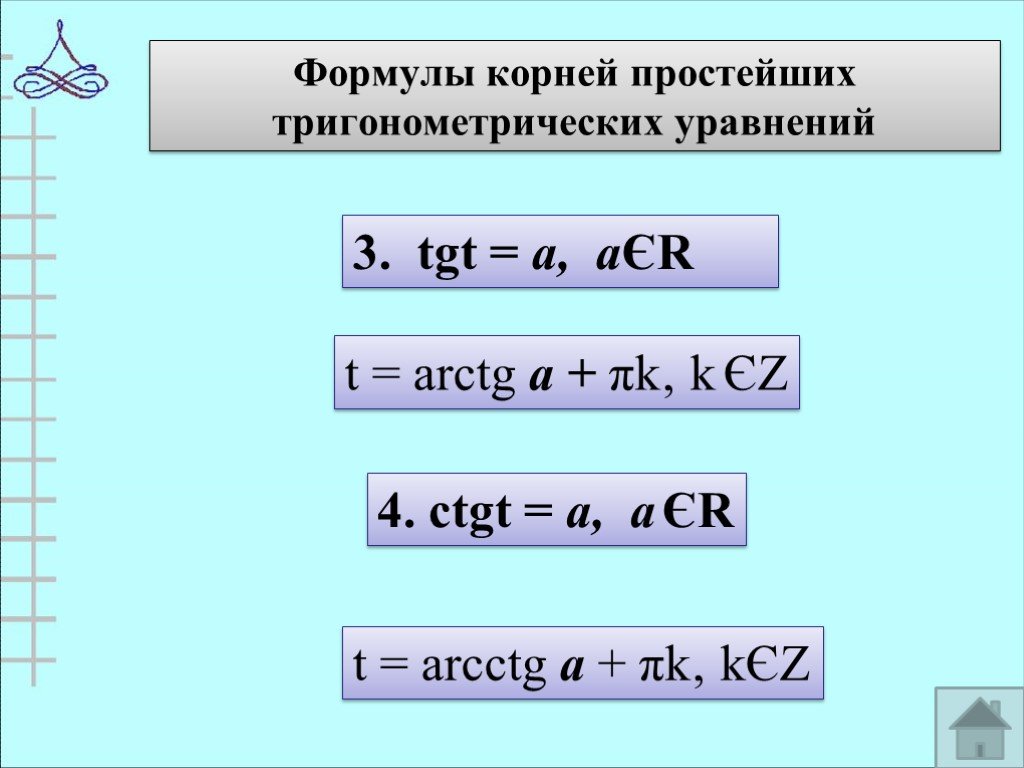
Примеры решения тригонометрических уравнений. Проверочная работа В заданиях 1-6 найдите значения аркфункций в заданиях 7-15 запишите решения простейших ...Методы решений тригонометрических уравнений
Цели урока:. Рассмотреть тригонометрические уравнения, решаемые с помощью: понижения степени введения вспомогательного угла и др. Разминка. Arcsin(a), ...Итоговый урок: решение систем уравнений
ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...меню для тригонометрических уравнений
Используемая литература. Алимов Ш.А. Алгебра и начала анализа 10-11 класс / Москва «Просвещение» 2002 год Тырымов А. А. методические пособия по математике ...Графическое решение уравнений
Установите соответствие:. А) парабола Б) ветвь параболы С) «галочка» Д) прямая. 4, 6 9 3. х у 0 1 х = 0. х = 0, х = 1. х = -2, 6 0 2 3 4 -2 6. . -2 ...8 класс "Решение квадратных уравнений"
. . . . . . «Уравнение – это золотой ключ, открывающий все математические тайны». . Цель: привести в систему знания о квадратных уравнениях и умение ...Графическое решение уравнений
АЛГЕБРА– 7 КЛАСС. ТЕМА: Графическое решение уравнений. Проверка домашнего задания. № 973 № 974. № 976 (а) построить функцию у = х2, построить функцию ...Решение диофантовых уравнений
Цели и задачи. Биография Диофанта Диофантовы уравнения с одной неизвестной Диофантовые уравнения первой степени Диофантовые уравнения высших степеней ...Графическое решение систем уравнений
Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...Графическое решение систем уравнений
Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...Графическое решение квадратных уравнений
Цель урока. формировать умение решать квадратные уравнения графическим способом. Решить уравнение х2 – 2х –3 = 0. Решение. I способ Построим график ...Решение задач на применение основных тригонометрических формул и преобразование выражений
Цели и задачи урока. Повторить основные тригонометрические формулы. Закрепить знания свойств синуса, косинуса, тангенса и котангенса. Научиться применять ...Графическое решение квадратных уравнений
Немного истории. Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений. Диофант Александрийский, Аль- Хорезми . Евклид Омар Хайям. ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...Конспекты
Общие методы решения тригонометрических уравнений
. ГБОУ ООШ с. Малое Ибряйкино. Похвистневского района Самарской области. Конспект урока для 10 класса на тему. «Общие методы ...Общие методы решения тригонометрических уравнений
. Муниципальное общеобразовательное учреждение. Малоибряйкинская основная общеобразовательная школа. Похвистневского района Самарской области. ...Методы решения тригонометрических уравнений
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 5 с углубленным изучением отдельных предметов. городского ...Решение дробных рациональных уравнений
8 класс. Тема « Решение дробных рациональных уравнений». Цель: закрепить изученный материал в ходе выполнения упражнений, развивать навыки решения ...Решение дробных рациональных уравнений
Муниципальное бюджетное общеобразовательное учреждение. «Новомихайловская средняя общеобразовательная школа». Татарского района Новосибирской области. ...Решение двухшаговых уравнений
Тема:. Решение двухшаговых уравнений. . . Цели:. 1) научить находить неизвестное слагаемое в уравнении вида: х+15=68:2;совершенствовать вычислительные ...Решение дробных рациональных уравнений
«. Решение дробно-рациональных уравнений». . Урок: алгебра 9 класс. Тема. :. . Решение дробных рациональных уравнений. Цель:. . познакомить ...Решение биквадратных уравнений
МУНИЦИПАЛЬНОЕ ОБРАЗОВАНИЕ ТАЗОВСКИЙ РАЙОН. Муниципальное казенное общеобразовательное учреждение. Тазовская школа – интернат среднего (полного) ...Методы решения тригонометрических уравнений
МОУ «Ангоянская средняя общеобразовательная школа». Открытый урок. по алгебре и началам анализа. 10 класс. Тема:. Методы решения тригонометрических ...Решение алгебраических уравнений
Тема: Решение алгебраических уравнений. Цели урока:. . систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:28 мая 2019
Категория:Математика
Классы:
Содержит:28 слайд(ов)
Поделись с друзьями:
Скачать презентацию






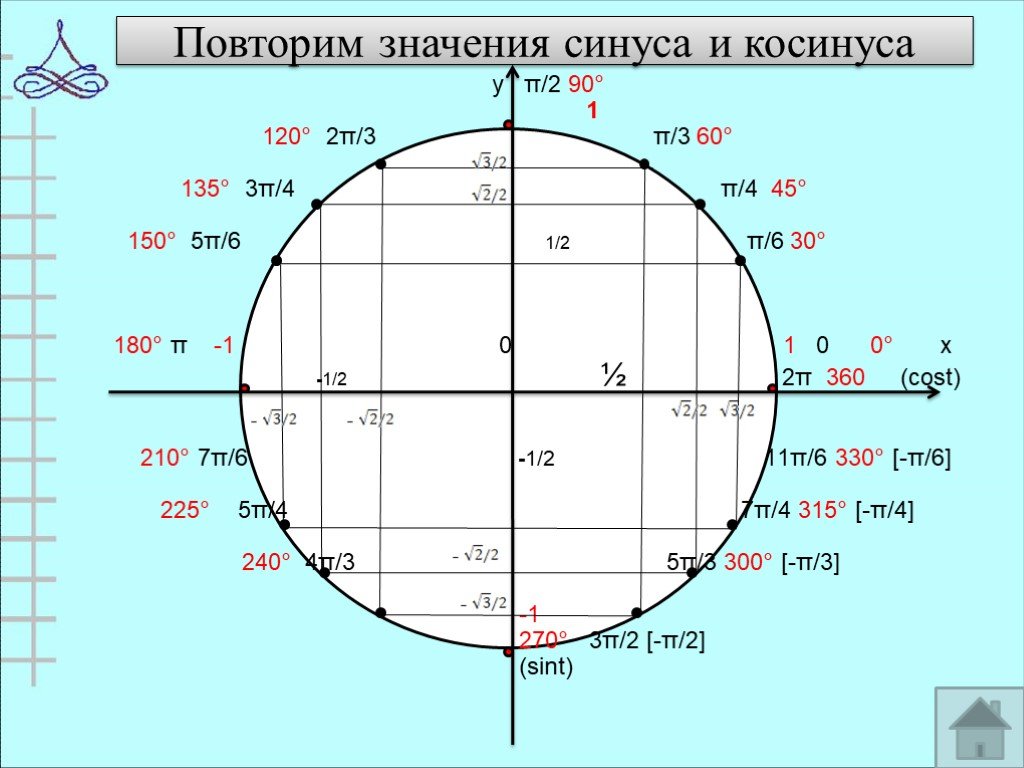





















![Повторим значения синуса и косинуса. у π/2 90° 1 120° 2π/3 π/3 60° 135° 3π/4 π/4 45° 150° 5π/6 1/2 π/6 30° 180° π -1 0 1 0 0° x -1/2 ½ 2π 360 (cost) 210° 7π/6 -1/2 11π/6 330° [-π/6] 225° 5π/4 7π/4 315° [-π/4] 240° 4π/3 5π/3 300° [-π/3] -1 270° 3π/2 [-π/2] (sint) Повторим значения синуса и косинуса. у π/2 90° 1 120° 2π/3 π/3 60° 135° 3π/4 π/4 45° 150° 5π/6 1/2 π/6 30° 180° π -1 0 1 0 0° x -1/2 ½ 2π 360 (cost) 210° 7π/6 -1/2 11π/6 330° [-π/6] 225° 5π/4 7π/4 315° [-π/4] 240° 4π/3 5π/3 300° [-π/3] -1 270° 3π/2 [-π/2] (sint)](https://prezentacii.org/upload/cloud/19/05/40460/images/thumbs/screen6.jpg)
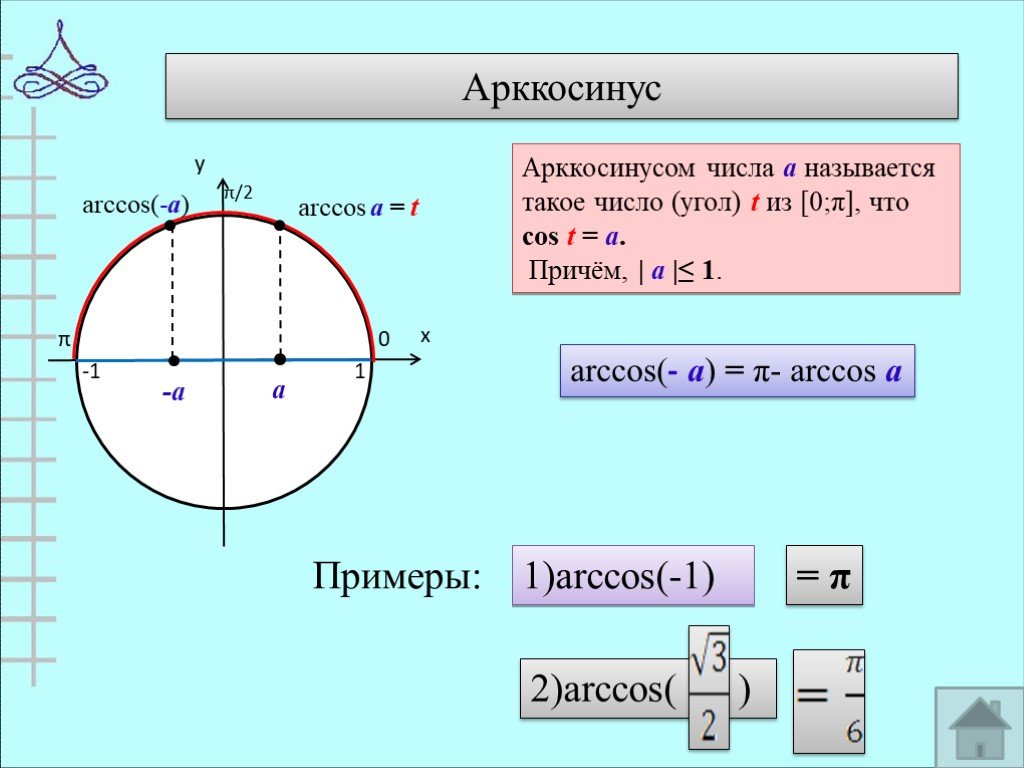
![Арккосинус 0 π 1 -1 arccos(-а). Арккосинусом числа а называется такое число (угол) t из [0;π], что cos t = а. Причём, | а |≤ 1. arccos(- а) = π- arccos а Примеры: 1)arccos(-1) = π 2)arccos( ) Арккосинус 0 π 1 -1 arccos(-а). Арккосинусом числа а называется такое число (угол) t из [0;π], что cos t = а. Причём, | а |≤ 1. arccos(- а) = π- arccos а Примеры: 1)arccos(-1) = π 2)arccos( )](https://prezentacii.org/upload/cloud/19/05/40460/images/thumbs/screen7.jpg)
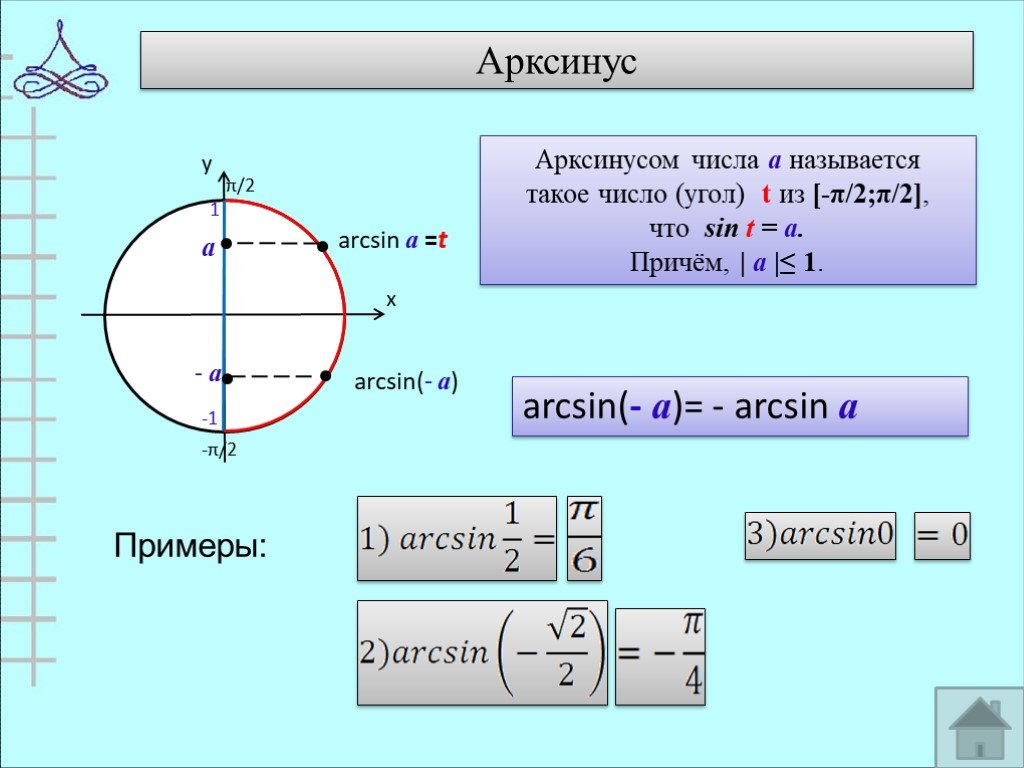
![Арксинус а - а arcsin(- а)= - arcsin а. Арксинусом числа а называется такое число (угол) t из [-π/2;π/2], что sin t = а. Причём, | а |≤ 1. Арксинус а - а arcsin(- а)= - arcsin а. Арксинусом числа а называется такое число (угол) t из [-π/2;π/2], что sin t = а. Причём, | а |≤ 1.](https://prezentacii.org/upload/cloud/19/05/40460/images/thumbs/screen8.jpg)

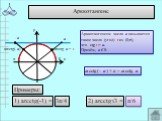


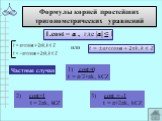
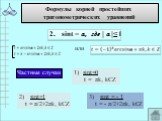

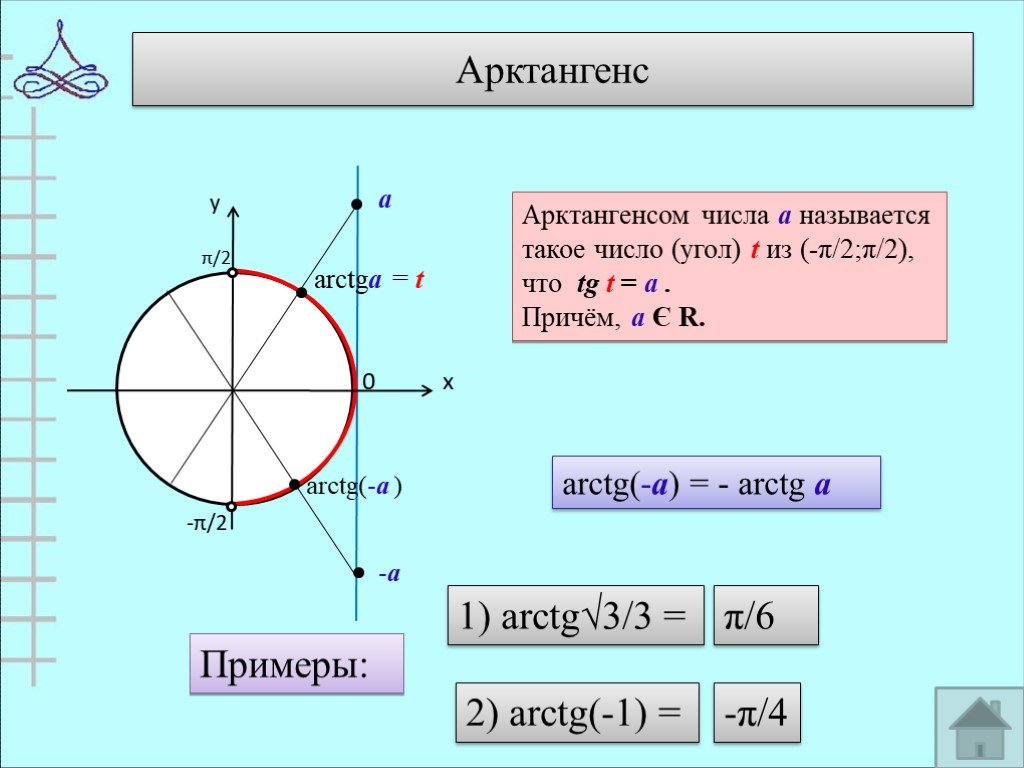
![При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x). 1) -1≤ 2х+1 ≤1 -2≤ 2х ≤0 -1≤ х ≤0 Ответ: [-1;0]. 2) -1≤ 5-2х ≤1 -6≤ -2х ≤ -4 2≤ х ≤3 Ответ: [2;3] При каких значениях х имеет смысл выражение: 1.arcsin(2x+1) 2.arccos(5-2x) 3.arccos(x²-1) 4.arcsin(4x²-3x). 1) -1≤ 2х+1 ≤1 -2≤ 2х ≤0 -1≤ х ≤0 Ответ: [-1;0]. 2) -1≤ 5-2х ≤1 -6≤ -2х ≤ -4 2≤ х ≤3 Ответ: [2;3]](https://prezentacii.org/upload/cloud/19/05/40460/images/thumbs/screen16.jpg)