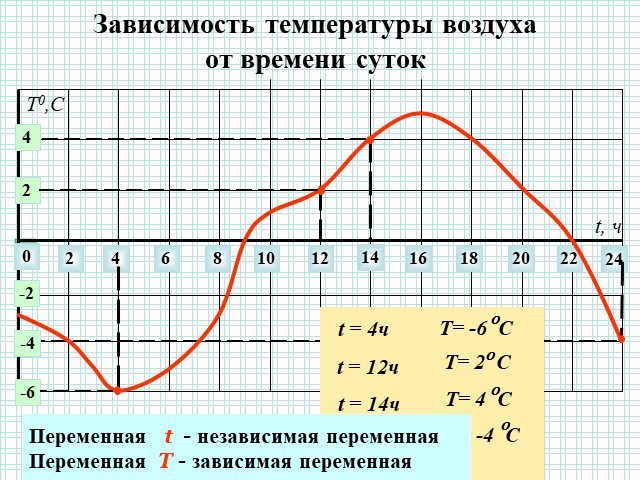
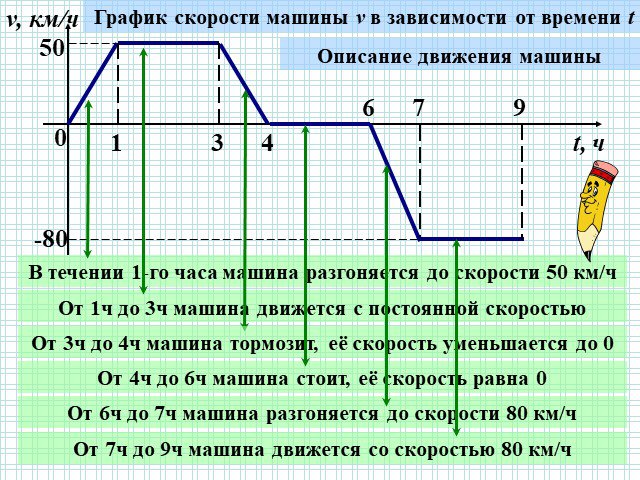
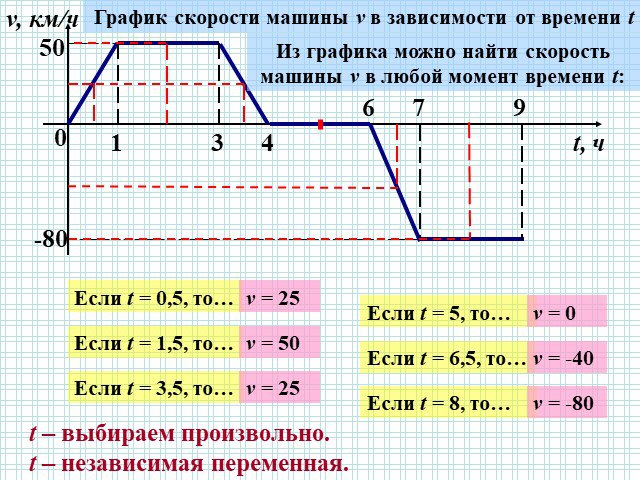
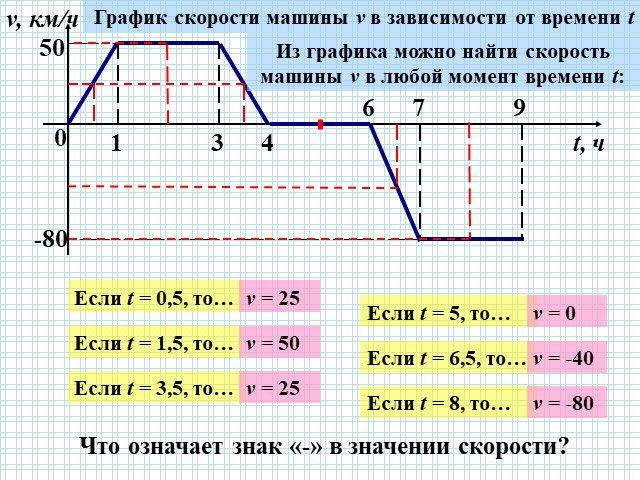
Презентация "Функция. График функции." по математике – проект, доклад
Презентацию на тему "Функция. График функции." можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
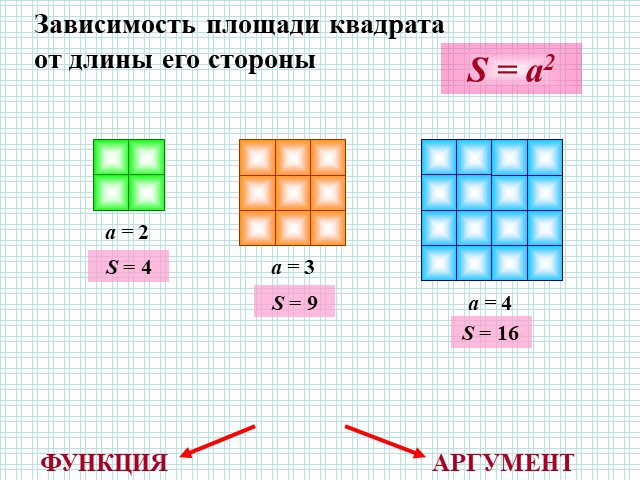
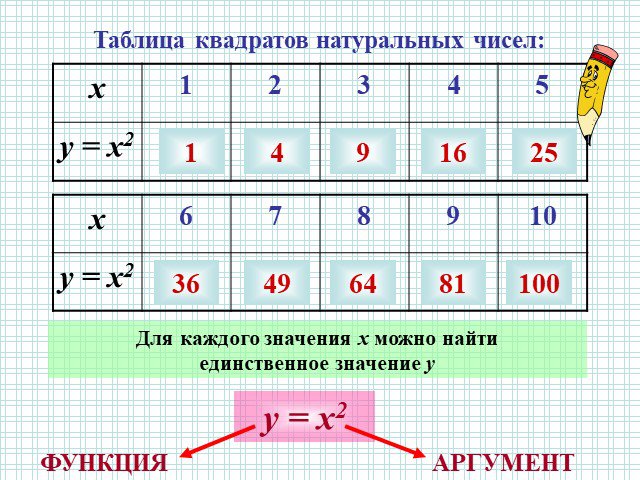
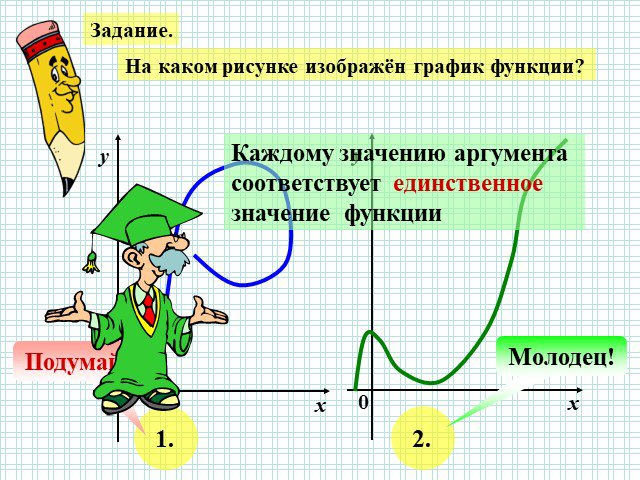
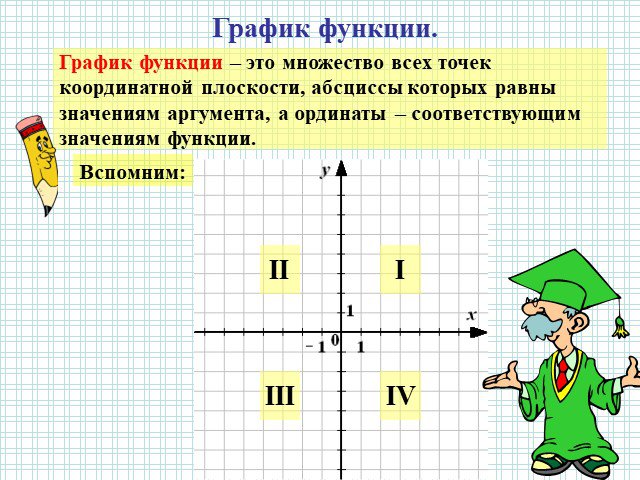
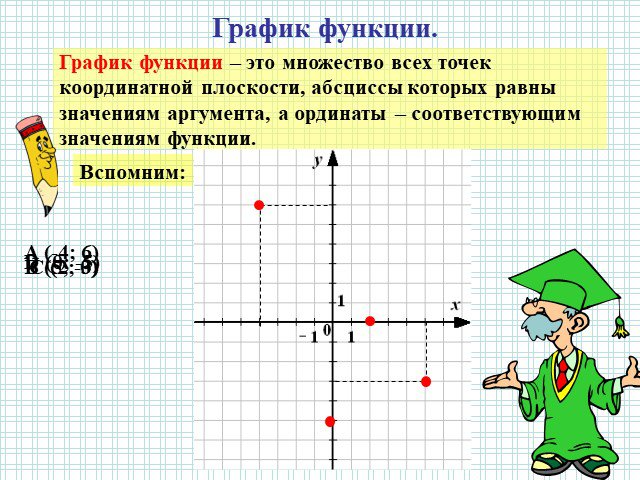
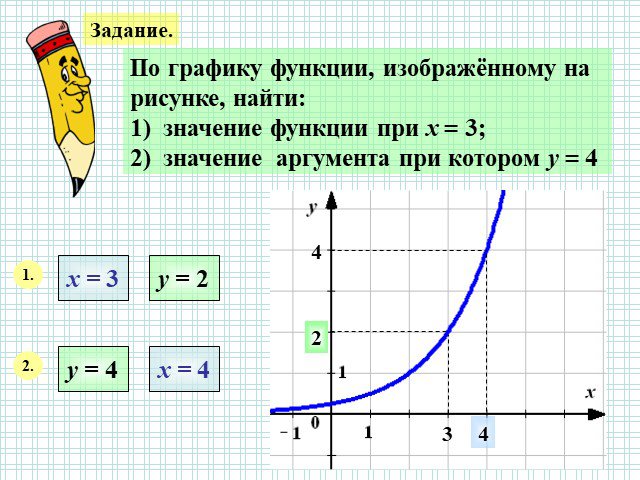
I Функция У=АХ², её график и свойства
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ...Построение графика квадратичной функции
Цели:. Формирование у учащихся умения строить график квадратичной функции в соответствии со схемой. определение. Квадратичной функцией называется ...Построение графика функции методом ее исследования с помощью производной
доцент кафедры математического образования Батан Любовь Федоровна. учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя ...Построение графика линейной функции вида у= kx + b
у = - 2х + 3 – линейная функция. Графиком линейной функции является прямая, для построения прямой нужно иметь две точки. х – независимая переменная, ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...Исследование функции и построение графика
ЕГЭ - 2014 Ответ: 3. Ответ: -0,25. Ответ: 7. Ответ: 2. . Ответ: 9. Ответ: 0. Ответ: -2. Ответ: 5. Ответ: 4. Ответ: -3. . Ответ: -12. . Исследование ...Построение графика квадратичной функции
Сдвиг графика функции y = ax2 вдоль оси y. y = x2 y = x2+1 x y. -2 1 0 y = x2 – 2. Сдвиг графика функции y = ax2 вдоль оси x. -3 y = (x+3)2. 2 y = ...Влияние коэффициентов а, b и с на расположение графика квадратной функции
Определите, график какой функции изображен на рисунке:. у = х² – 2х – 1; у = –2х² – 8х; у = х² – 4х – 1; у = 2х² + 8х + 7; у = 2х² – 1. у = ½х² – ...Взаимное расположение графиков линейной функции
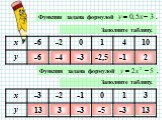
Разбейте функции, заданные формулами, на группы:. у = 2х - 3; у = х2 - 3; у = - 5х; у = 4 - 0,5х; у = - х +2; у=15х;. 7. 8. 9. 10. у = х (1 - х). ...Зачем нужно строить асимптоты графиков дробно-рациональной функции?
В работе сделан экскурс в историю возникновения понятия асимптоты, сделан сравнительный анализ различных определений асимптоты. Рассматривается построение ...Исследование графика функции с помощью производной.
Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4] функции. -7 4 Y=f'(x) проверка 0 1 X Y Y=f‘(x). ...Графики и функции в основной школе
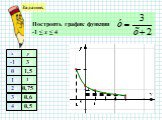
Постройте график функции. и найдите все значения а, при которых прямая у=а имеет с графиком данной функции ровно одну общую точку. 1. О чем говорится ...Как построить график функции у = mf(x),если известен график функции у = f(x)
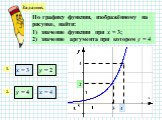
Вид преобразования: параллельный перенос. у = х у = 2х у =½х. у = 4х у =¼х. у =½x² у =2 х². у=5х² у = х². что произойдет с графиками при умножении ...Касательная к графику функции
Содержание. 1. Определение касательной к графику функции. 2. Уравнение касательной к графику функции в общем виде. 3. Алгоритм составления касательной ...Как построить график функции y=f(x+l)+m из графика функции y=f(x)
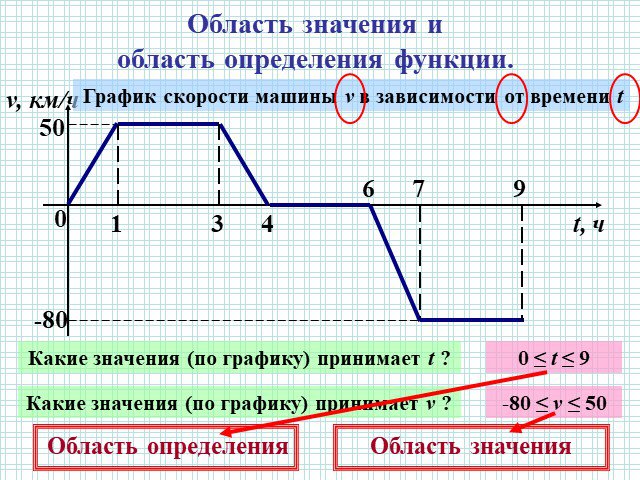
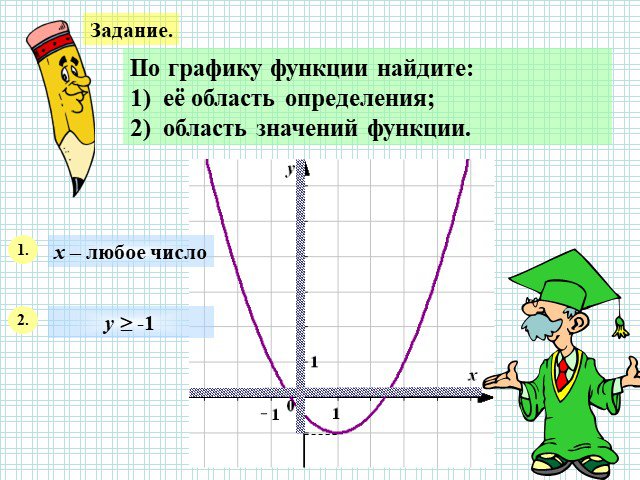
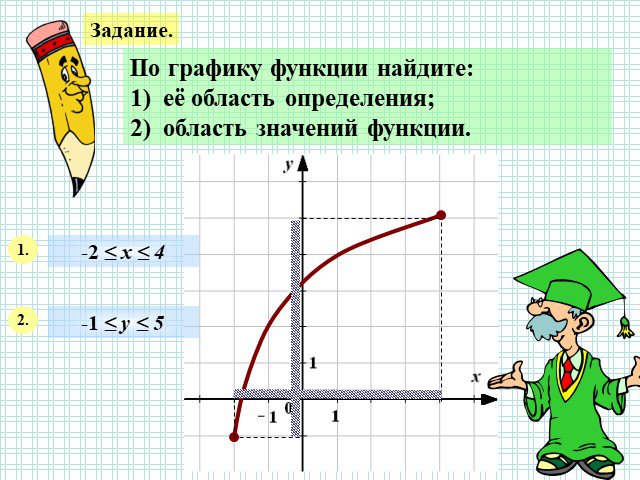
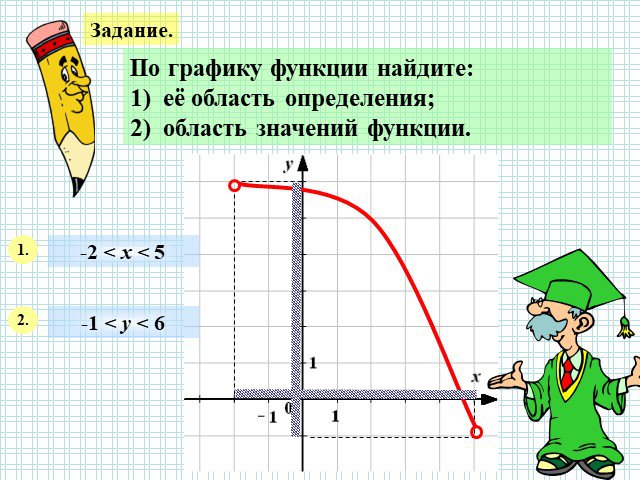
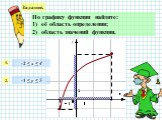
x y 1 0 6 3. Устная работа на повторение. 1) [-1;3] 2) [0;6] 3) [-2;6] 4) [0;3]. Найдите область определения функции. -2. Найдите область значений ...График квадратичной функции. Неравенства с одной переменной
Квадратичная функция и ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax² + bx + c, где х – независимая ...Как построить график функции y=f(x+L)+m, если известен график функции y=f(x)
ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x). Цель урока: Научиться строить график функции y=f (x + L) ...Алгоритм построения графика квадратичной функции
1)направление «ветвей» параболы. если а>0, то «ветви» параболы направлены вверх; если а 0 - «ветви» параболы направлены вверх;. 2)Нахождение координат ...График линейной функции
График линейной функции. Цели урока:. Обучающие: 1. Учить строить график линейной функции; 2. Заполнять по графику таблицу значений х и у; 3. Изображать ...График линейной функции
1. Как называется функция у = - 2 х - 3? 2. Уравнение прямой линии имеет вид у = К х + b. Для функции у = – 7 + 2 х запишите, чему равны К и b. 3. ...Конспекты
Квадратичная функция. Построение графика квадратичной функции
Конспект урока. Тема урока:. Квадратичная функция. Построение графика квадратичной функции . Класс:. 8. Цели урока:. . . 1. Формирование ...Логарифмическая функция. График и свойства логарифмической функции
Класс: 11. Тема урока. : Логарифмическая функция. График и свойства логарифмической функции (Слайд 1,2). Цели урока:. . 1.Ввести определение ...Число е. Функция у=е, её свойства и график
П х. . ЛАН-КОНСПЕКТ УРОКА. . «Число е. Функция у=е, её свойства и график» . ФИО. . . Грудинина Мария Михайловна. . . . ...Числовые функции их свойства и графики
Технологическая карта урока математики в 9 классе по теме: «Числовые функции их свойства и графики», учебник А.Г.Мордковича. Урок развивающего контроля ...График квадратичной функции и модуль
Администрация города Улан - Удэ. Комитет по образованию. МАОУ «Средняя общеобразовательная школа № 25». Урок алгебры в 9 классе. ...График квадратичной функции
МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 17. КУРГАНИНСКИЙ РАЙОН. Тема: «График квадратичной функции». ...Функция. Обобщение и расширение знаний о свойствах функции
Урок – «бенефис». Функция. Свойства функции. Учитель: Вундцеттель Ж.А. Тема урока: Функция. Обобщение и расширение знаний о свойствах функции. ...Взаимное расположение графиков линейной функции
Открытый урок по алгебре в 7 классе на тему: «Взаимное расположение графиков линейной функции». Напомните пожалуйста, что мы изучали на прошлом ...Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения
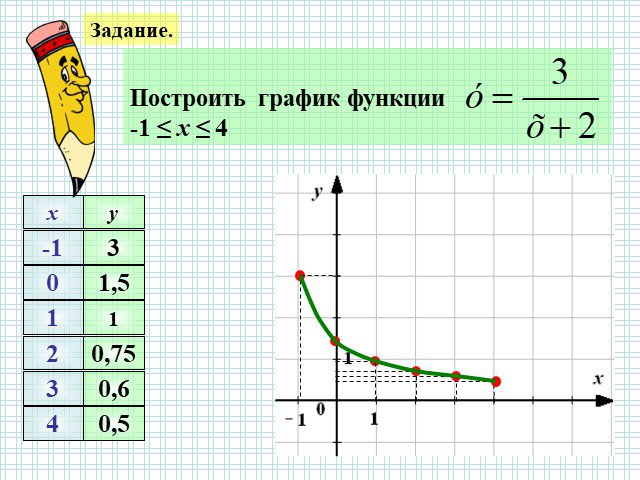
Предмет:. алгебра 10 кл. Тема урока:. «Преобразование графика тригонометрической функции у = sin. x. путем сжатия и расширения». Тип урока:. ...Функция у=к/х и её график
Открытый урок по алгебре в 8 А классе. . учителя Никитиной Ирины Александровны. Тема. :. Функция у=к/х и её график. (2-й урок в теме). Цель. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию