Презентация "Квадратичная функция" по математике – проект, доклад

Скачать презентацию (1.42 Мб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Презентацию на тему "Квадратичная функция" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 13 слайд(ов).

Скачать презентацию (1.42 Мб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

ИНТЕГРИРОВАННЫЙ УРОК ПО АЛГЕБРЕ И ИНФОРМАТИКЕ В 9 КЛАССЕ Учитель математики и информатики средней школы №6 г. Пятигорска Аветисян Жанна Георгиевна

Слайд 2

Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании Аристотель

Слайд 3

Устный опрос Сформулировать определение квадратичной функции; Что является графиком квадратичной функции? Сформулировать свойства квадратичной функции у=ах2 при а>0, a

Слайд 4

Задание 1

Слайд 5

Практическое выполнение задания в тетради В одной системе координат построить графики функций в тетрадях: А)у = 1/2 x2; y = 1/2x2 +4; y =1/2x2 -3; Б)у=-1/3х2 , y = -1/3(x-2)2 , y = -1/3(x+3)2 ,

Слайд 6

Задание 1 Построить в одной системе координат графики функции y=x2 , y=x2-5 и y=x2+5

Слайд 7

Задание 2 Построить в одной системе координат графики функций у=2х2, у=2(х-5)2, у=2(х+4)2

Слайд 8

Задание 3 Построить в одной системе координат графики функций у=2х2 ,у= 2(х-5)2+3, у=-2(х+4)2-5

Слайд 9

Проверь себя Задание 2 Задание 3

Слайд 10

Вывод: График функции у=ах2 +n является параболой, которую можно получить из графика функции у=ах2 с помощью параллельного переноса вдоль оси у на n единиц вверх, если n>0, или на -n единиц вниз, если n

Слайд 11

Вывод : График функции у=а(х-m)2 является параболой, которую можно получить из графика функции у=ах2 с помощью параллельного вдоль оси х на m единиц вправо, если m>0, или –m единиц влево, если m

Слайд 12

Вывод: График функции у=а(х-m)2 +n является парабола, которую можно получить из графика функции у=ах2 с помощью двух параллельных переносов: сдвига вдоль оси х на m единиц вправо, если m>0, или на –m единиц влево, если m0, или на –n вниз, если n

Список похожих презентаций

Квадратичная функция.

Квадратичная функция:. Квадратичной функцией называется функция, которую можно записать формулой вида y=ax2+bx+c, где x – независимая переменная, ...

Квадратичная функция. Графики функций

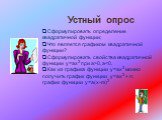
Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании Аристотель. Устный опрос Сформулировать определение квадратичной ...

Квадратичная функция, её свойства и график

Определение. Квадратичной функцией называется функция, которую можно задать формулой вида y = ax2 + bx + c, где x – независимая переменная, a,b и ...

Квадратичная функция: построение графика

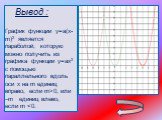
Содержание:. y x 0. График функции y = a x. 2 при a=1 при a= -1 1 2 3 4 5 6 -6 -5-4-3-2-1 1 4 9 -9 -4. 0 1 2 3 4 5 6 У= X. Построить график функции ...

Квадратичная функция, её свойства и график

Вспомнить свойства функций у = kx +b и у = х², их графики. Изучить свойства функции у = kx², у = - kx² и научиться строить график. Научиться по графику ...

Квадратичная функция, её свойства и график

Цели:. ввести понятие квадратичной функции; научится строить график функции у=ах2 + ах +с и описывать свойства данной функции по графику; установить ...

Квадратичная функция и ее график

Функция y=ax2,ее график. Квадратичной функцией называется функция, которую можно задать формулой вида y=ax2+bx+c , где x- независимая переменная, ...

Квадратичная функция и ее свойства

Определение. Функция вида у = ах2+bх+с, где а, b, c – заданные числа, а≠0, х – действительная переменная, называется квадратичной функцией. Примеры: ...

Квадратичная функция

Жизнь украшается двумя вещами: занятием математикой и ее преподаванием. С. Пуассон. Тема урока: «Квадратичная функция». Цель урока:. Обобщить знания ...

Квадратичная функция и ее график

Выберите правильный ответ:. 1. где x - независимая переменная, n-натуральное число. 2. где х - независимая переменная, a,b,c – некоторые числа, причем ...

Квадратичная функция

План:. 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Определение:. Квадратичной функцией ...

Квадратичная функция

История параболы. Математики Древней Греции отк- рыли параболу ещё в 260-170 г.г. до нашей эры при изучении коничес- ких сечений. Уже в 17 веке Галилео ...

Квадратичная функция

План:. Урок 1 Определение квадратичной функции; Функция вида Функция вида Урок 2 Функция вида Функция вида Функция вида Урок 3 Функция вида Урок 4 ...

Квадратичная функция. Ее свойства и график

В математике есть своя красота, как в живописи и поэзии. (Н.Е.Жуковский). y= ax2 +bx + c. где: a,b,c – числа Х – независимая переменная а 0. Определение ...

Квадратичная функция. Её свойства и график

Определение квадратичной функции. Функцию вида y = ax2 + bx + c, где a, b, c - произвольные числа, причём a ≠ 0, называют квадратичной функцией («a» ...

Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной. Содержание. Квадратный ...

Прямая и обратная пропорциональность Линейная функция

Прямая y = − x Биссектриса II и VI координатных углов. Прямая пропорциональность y = kx Графиком является прямая, проходящая через начало координат ...

Показательная функция урок

Цели урока: Образовательная: ввести понятие показательной функции, рассмотреть ее свойства и построить график. Применить изученные свойства показательной ...

Показательная функция, ее свойства и график

Свойства показательной функции:. Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией. Область определения показательной ...

Показательная функция

Определение. Функцию вида называют показательной функцией. Основные свойства. График функции Кривая называется экспонентой а>1. 0. Геометрическая ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.