Презентация "Линейная функция" по математике – проект, доклад
Презентацию на тему "Линейная функция" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
Линейная функция и равномерное прямолинейное движение
Математика – это язык, на котором говорят все точные науки. Н.И.Лобачевский. Слеп физик без математики. М.В.Ломоносов. Устный опрос. Является ли заданное ...Урок Линейная функция
Цель урока:. Обобщить материал, который мы изучали в течение 15 уроков и продемонстрировать умение использования наших знаний. Шкалирование ЗНАНИЯ ...Линейная функция и линейные уравнения вокруг нас
1. Линейное уравнение с одной переменной 2. Алгоритм решения линейного уравнения. Примеры уравнений 3. Примеры решения задач с помощью линейных уравнений ...Линейная функция"
Линейная функция. Учитель математики МБОУ сош№3 г Сосновый Бор Ленинградской обл Иванова Н.Л. ЦЕЛЬ УРОКА:. Обобщение и закрепление знаний по теме ...Линейная функция и ее график
Условия игры:. Класс разбить на шесть команд. В каждой команде один участник, один помощник, два-три болельщика. За правильный ответ команда получает ...Линейная функция и ее график
Цели урока:. Познакомиться с понятием линейной функции Выработать умение строить график линейной функции Познакомиться с математическими моделями ...Линейная функция и ее график
Какие функции являются линейными?s = 2t – 8 u = -3v + 1 у = 7 – 5х у = 9х f = 5 – g3. Линейная функция: Назвать k и b. у = 5х + 8 k = 5; b = 8 у ...
Линейная функция и ее график
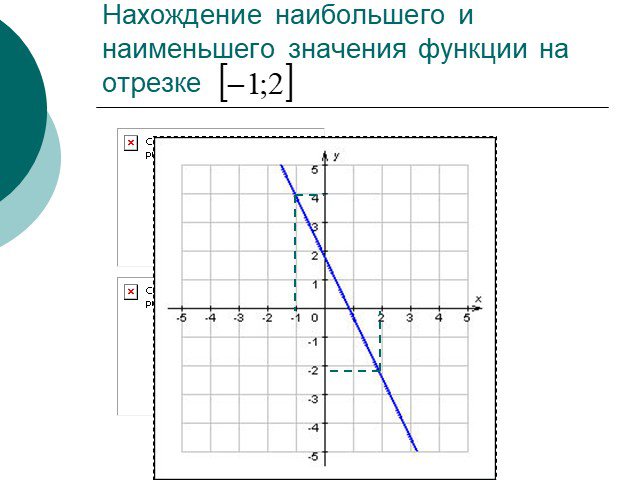
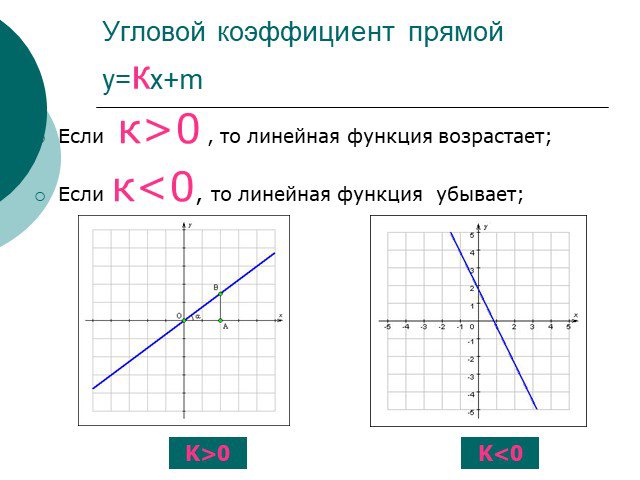
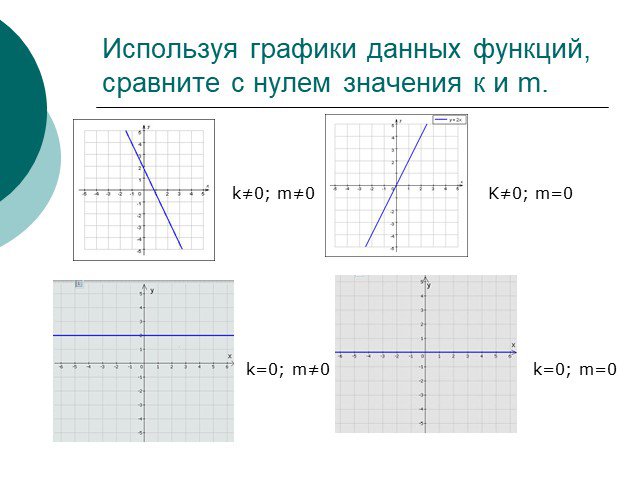
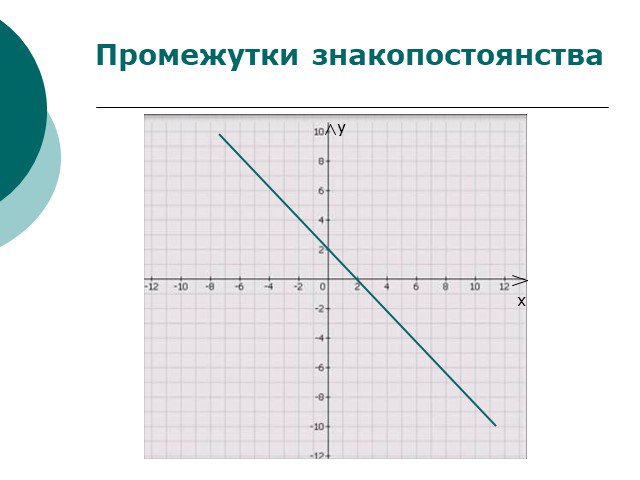
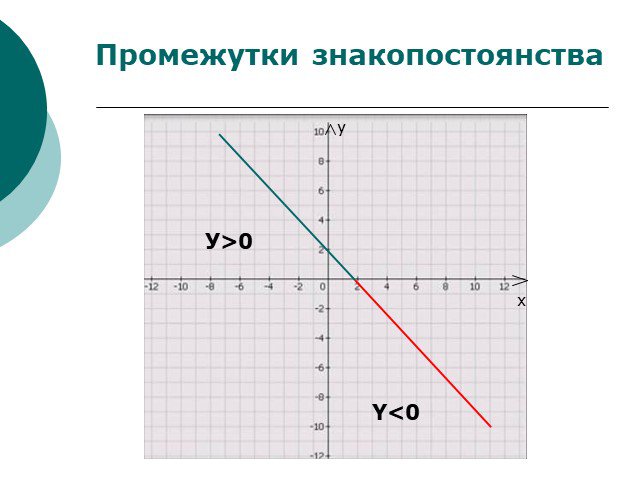
Что общего в этих изображениях? В чем различие рисунков? Линейная функция у=кх+l. возрастающая убывающая постоянная к >0 l >0 к< 0 l< 0 к >0 l< 0 ...Линейная функция и её график
Цель урока: Сформировать представление о числовой функции на примере линейной функции, с её графиком и алгоритмом его построения по двум точкам. ЗАДАЧИ: ...Обобщающий урок по теме « Линейная функция»
1) Какая функция называется линейной? Область определения и область значения линейной функции? Линейной функцией называется функция, которую можно ...Линейная функция
Цели:. Напомнить понятие координатной плоскости. Рассмотреть изображение точки на координатной плоскости. Дать понятие об уравнении с двумя переменными, ...Линейная функция
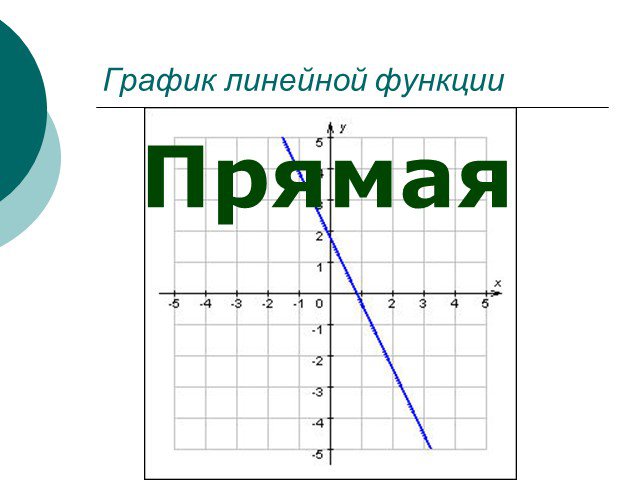
Определение линейной функции. Линейной функцией называется функция вида Y=kx+b, где k и b некоторые числа. График линейной функции. Графиком линейной ...Линейная функция
Функция, заданная формулой , где k, b числа, x аргумент, называется линейной. Определение. График линейной функции. Графиком линейной функции является ...Линейная функция
Линейная функция Определение линейной функции Свойство линейной функции Описание График линейной функции График 1 (рис. 1) Пример 1 Пример 2 Замечание ...Линейная функция
Цели урока:. Обобщить знания по теме «Линейная функция» и «Равномерное прямолинейное» движение». Построение целостной системы знаний через межпредметные ...Линейная функция
Определение. Линейной функцией называется функция, задаваемая формулой вида: y = kx + b, где k и b - некоторые числа. Прямопропорциональная зависимость. ...Линейная функция в рисунках
Авторы проекта: учащиеся 7-го класса: Горин Роман, Свешникова Екатерина, Спасюк Анастасия, Спренгель Дарья. Руководители: Кузнецова Галина Алексеевна ...Линейная функция и её график
Функция вида y = kx +b, где k и b числа, а x и y переменные, называется линейной функцией. x – независимая переменная (аргумент) y – зависимая переменная ...Прямая и обратная пропорциональность Линейная функция
Прямая y = − x Биссектриса II и VI координатных углов. Прямая пропорциональность y = kx Графиком является прямая, проходящая через начало координат ...Линейная функция
Содержание. Определение График Взаимное расположение графиков линейных функций Частные случаи Вопросы для повторения. Функция, заданная формулой , ...Конспекты
Линейная функция и ее свойства
Кочуева Людмила Николаевна. МКОУ «Рождественская ООШ» п. Тим. Учитель математики. Разработка открытого урока по математике в 7 классе. . ...Линейная функция, ее график, свойства
. «Линейная функция, ее график, свойства». (урок алгебры в 7 классе). Боброва Наталья Александровна. учитель математики. . ГОУ СОШ №19 им. ...Линейная функция и ее график
ПЛАН-КОНСПЕКТ УРОКА «Линейная функция и ее график». (Тема урока). . . ФИО (полностью). . Шинкарюк Светлана Юрьевна. . . . ...Линейная функция и её применение
Наименование ОУ:. МБОУ СОШ №12 г. Саров. ФИО автора:. Градова Юлия Геннадьевна. Должность:. учитель математики. . Бизнес-игра «УМА ПАЛАТА». ...Линейная функция и её график
ПЛАН-КОНСПЕКТ УРОКА «Линейная функция и её график». . ФИО (полностью): Одышева Ольга Валентиновна. . . . . Место работы: ...Линейная функция и ее график
Урок по алгебре в 7-м классе на тему: "Линейная функция и ее график". . Вид урока. : комбинированный. Цели урока:. Образовательные. Повторить ...Линейная функция и ее график
Яковлева Ангелина Андреевна, учитель математики. МБОУ «СОШ №19» г.Новочебоксарск. Открытый урок по теме «Линейная функция и ее график». 7-а ...Линейная функция и её график
Разработка урока на т. ему:. «Линейная функция и её график». Цели урока:. . Обучающие:. 1. Научить учащихся строить графики линейной функции;. ...Линейная функция и ее график
Урок алгебры в 7 классе. . на тему "Линейная функция и ее график". . Цели:. . применение возможностей программы GeoGebra. и интерактивной. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:17 января 2013
Категория:Математика
Автор презентации:Неизвестен
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию









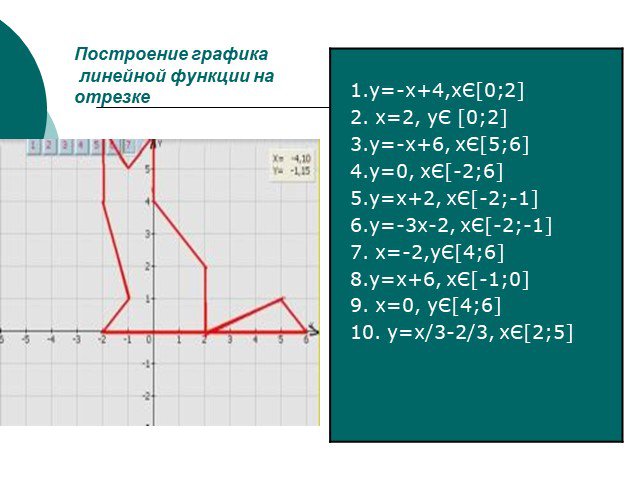
















![Домашнее задание. Построить отрезки в одной системе координат. 1. у=-2, хЄ[-4;-2] 2. х=-4, уЄ [-4;-2] 3. у=-х-8, хЄ[-4;-3] 4. у=-5, хЄ[-3;1] 5. у=х-6, хЄ[1;2] 6. х=2, уЄ[-4;1] 7. у=-х+3, хЄ[1;2] 8. у=2, хЄ[-2;1] 9. х=-2, уЄ [2;4] 10. у=4, хЄ[-2;2] 11. х=2, уЄ[4;6] 12. у=6, хЄ[-4;2] 13. х=-4, уЄ[0;6] Домашнее задание. Построить отрезки в одной системе координат. 1. у=-2, хЄ[-4;-2] 2. х=-4, уЄ [-4;-2] 3. у=-х-8, хЄ[-4;-3] 4. у=-5, хЄ[-3;1] 5. у=х-6, хЄ[1;2] 6. х=2, уЄ[-4;1] 7. у=-х+3, хЄ[1;2] 8. у=2, хЄ[-2;1] 9. х=-2, уЄ [2;4] 10. у=4, хЄ[-2;2] 11. х=2, уЄ[4;6] 12. у=6, хЄ[-4;2] 13. х=-4, уЄ[0;6]](https://prezentacii.org/upload/cloud/13/01/1600/images/thumbs/screen16.jpg)






























