Презентация "Усечённая пирамида" по математике – проект, доклад
Презентацию на тему "Усечённая пирамида" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
Пирамида. Усечённая пирамида
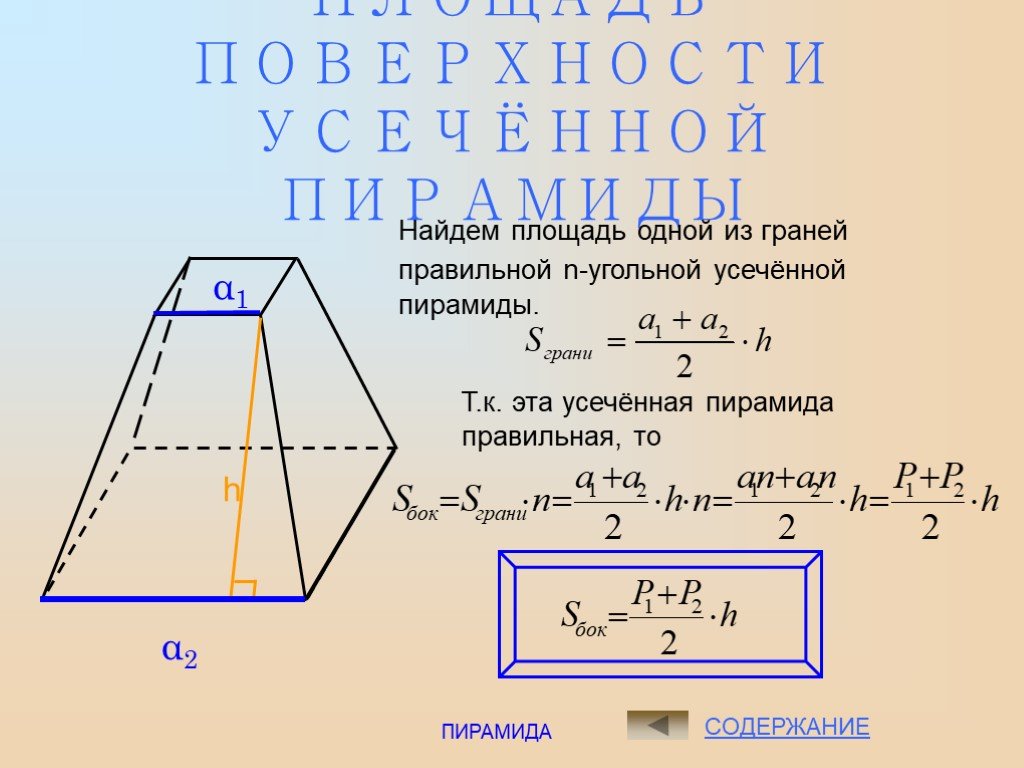
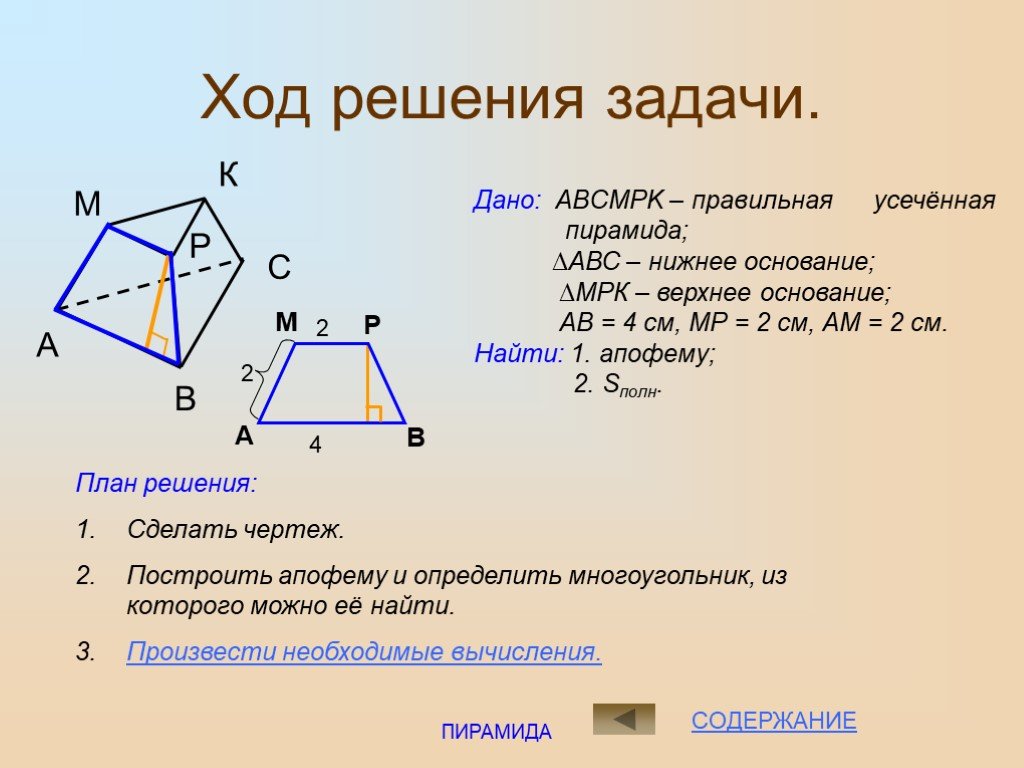
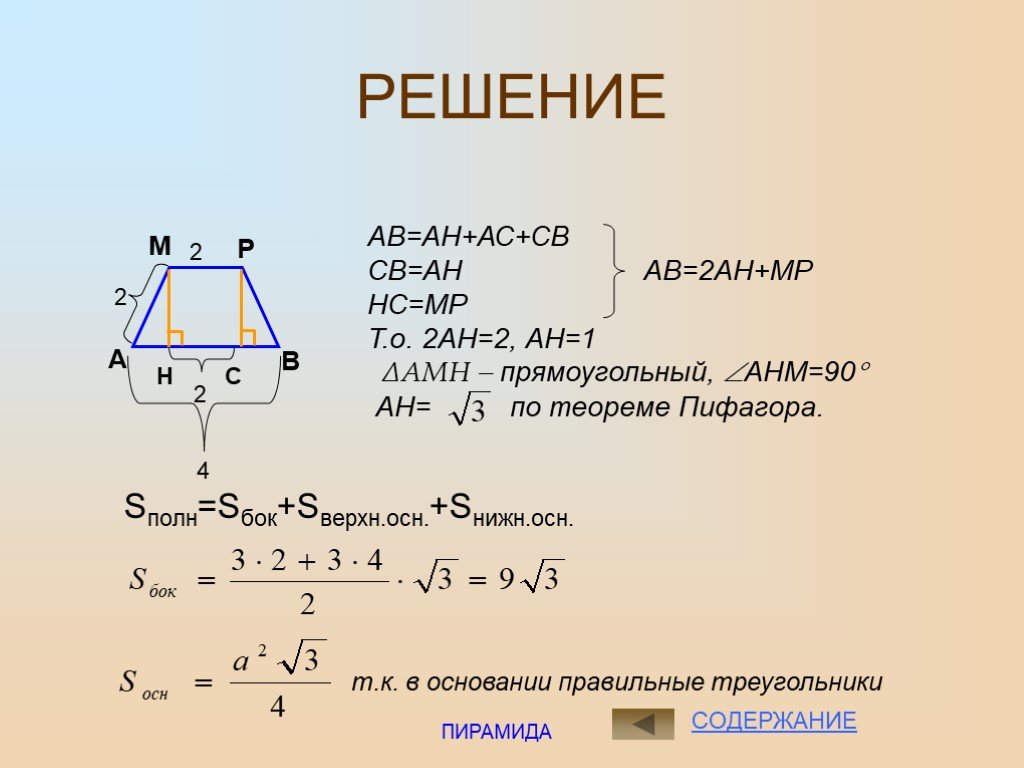
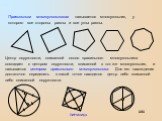
Архитектура и геометрия. . . . . . Многоугольник РА1А2А3….Ап основание пирамиды. Треугольники А1РА2, А2РА3 … боковые грани. Р –вершина пирамиды. РН ...Пирамида. Построение пирамиды и её плоских сечений. Усечённая пирамида. Правильная пирамида.
Что такое пирамида? Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.), а остальные ...Усечённая пирамида
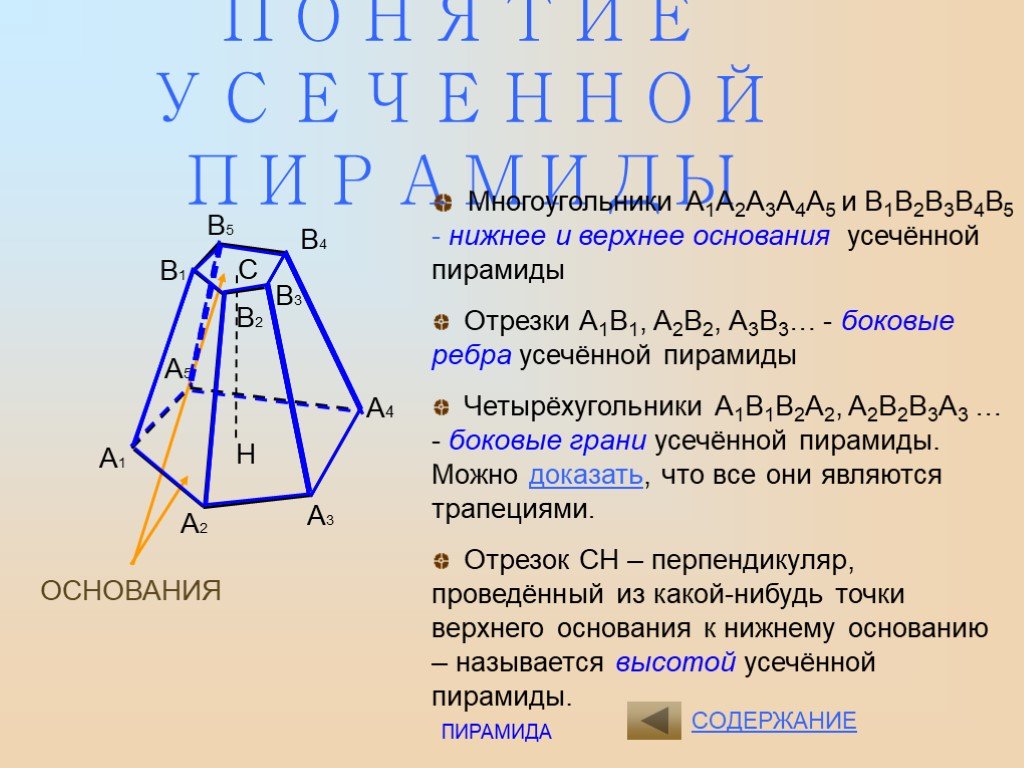
Многогранник, составленный из многоугольника A1A2…An и n треугольников называется n-угольной пирамидой. Многоугольник A1A2…An называется основанием ...Что такое пирамида ?
Термин “пирамида” заимствован из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского ...Фигура пирамида
Содержание. 1 История развития геометрии пирамиды 2 Элементы пирамиды 3 Развёртка пирамиды 4Свойства пирамиды 5Теоремы, связывающие пирамиду с другими ...Правильная пирамида
Тема урока: «Правильная пирамида». Цели урока:. 1. Познакомиться с понятием «правильная пирамида» и ее основными элементами. 2. Рассмотреть виды пирамид. ...Правильная пирамида
Цели урока:. введение понятия правильной пирамиды; рассмотрение свойств правильной пирамиды; введение понятия апофема; рассмотрение задач на нахождение ...Правильная пирамида
A D C B O K T E. В правильной четырехугольной пирамиде известны длина стороны основания 2 и длина высоты 2. Найдите: а) объем пирамиды; б) площадь ...Конус, пирамида, призма, цилиндр.
Цели урока. Учить учащихся навыкам и умениям определять название геометрических тел, мысленно расчленять предметы на составляющие его геометрические ...Геометрия пирамида
Цель. Обобщить, расширить и углубить сведения о пирамиде. Задачи:. Изучить дополнительные источники и собрать исторический и занимательный материал ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 мая 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию