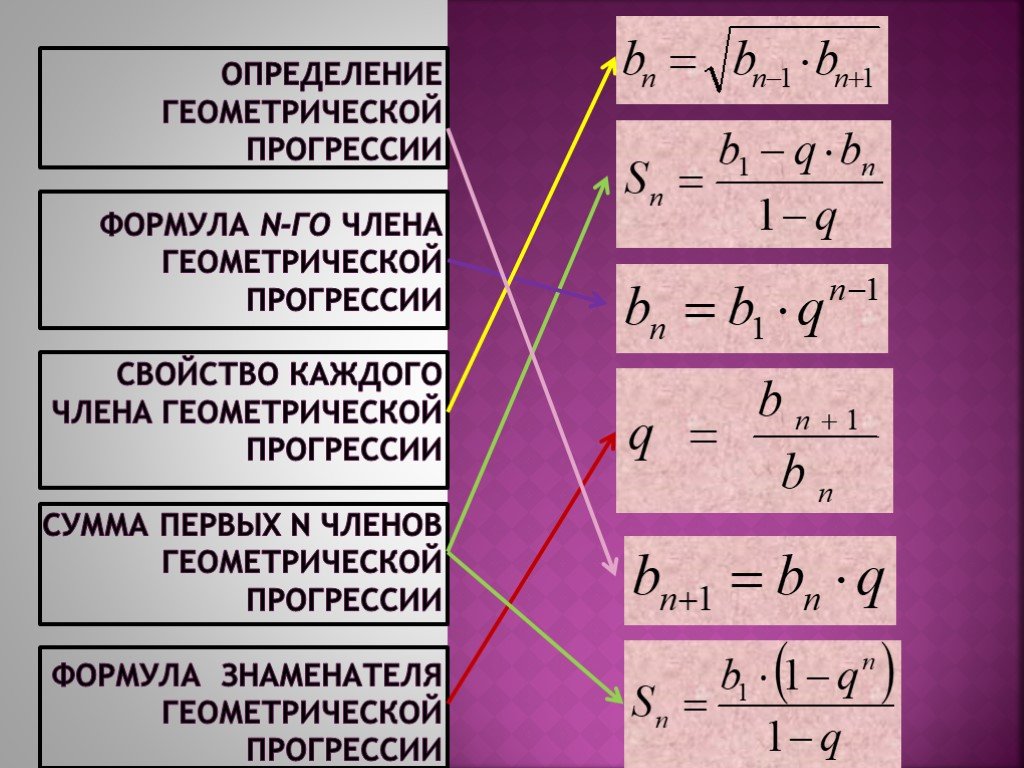
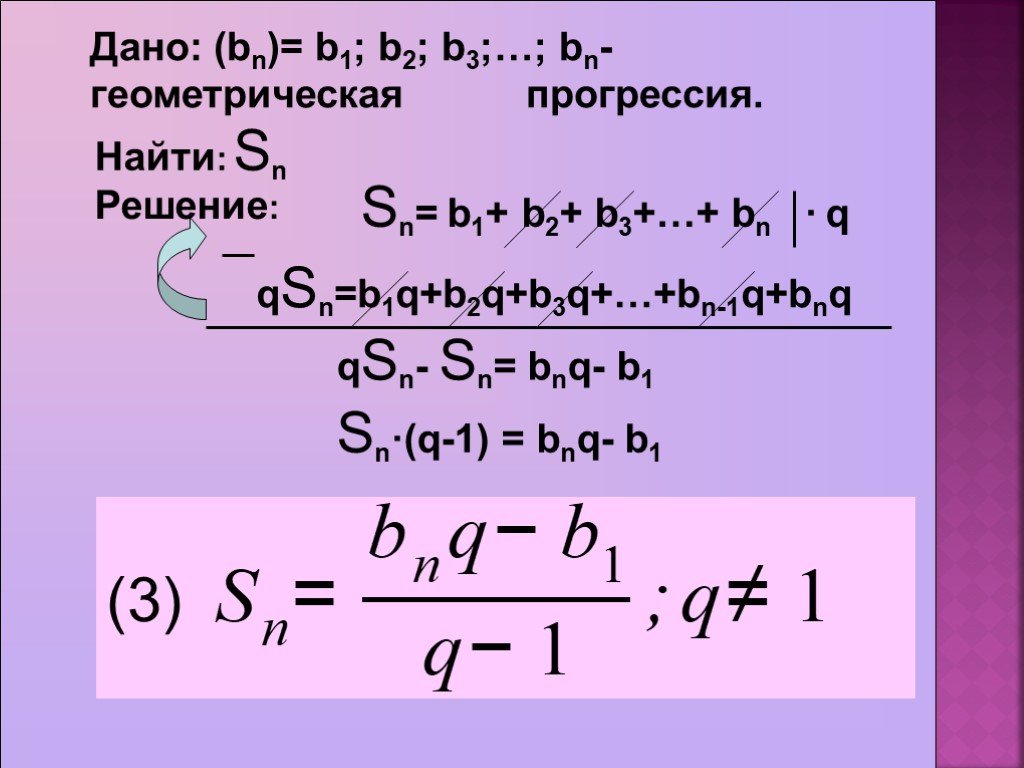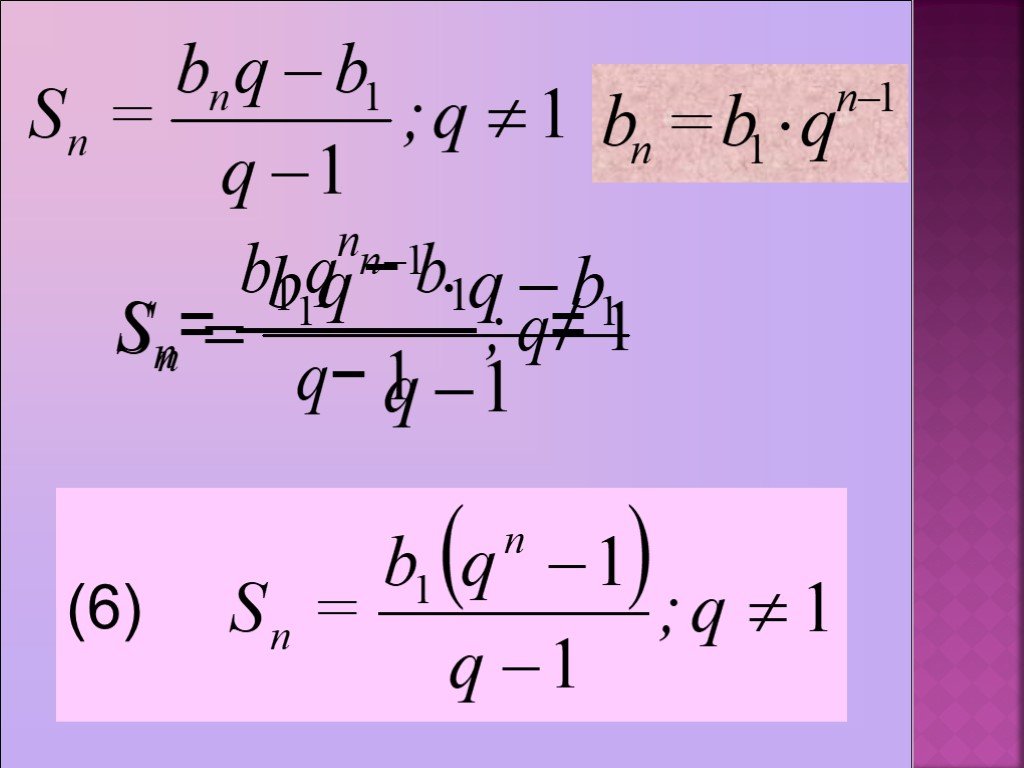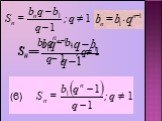Презентация "Формулы для решения задач на прогрессии" по математике – проект, доклад
Презентацию на тему "Формулы для решения задач на прогрессии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 40 слайд(ов).
Слайды презентации
Список похожих презентаций
Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Арифметика Л.Ф. Магницкого. Задачи на сплавы и смеси
Цели моей работы. Познакомиться с биографией Леонтия Филипповича Магницкого Научиться решать задачи на сплавы, находить процентное содержание веществ ...Викторина по математике для 5-6 классов
1.Половина-треть числа. Какое это число? Ответ: 3/2. 2.За книгу заплатили 60 рублей. И ещё 1/3 стоимости книги. Сколько стоит книга? 90 рублей. 3.Как ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Аналитические методы решения логарифмических уравнений
Цели урока:. Обобщить и систематизировать изученные методы решения логарифмических уравнений Выявить особенности каждого метода Выяснить, всегда ли ...Аналитический и численный методы решения систем уравнений с параметром
АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Блок-схема для решения квадратных неравенств
Неравенства второй степени вида. D. D=0 x=m m. D>0 m n. . . . . . . . Нет решения. . . . . . . . . Тренажер. решение квадратных неравенств. Варианты ...Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат
Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...Арифметическая прогрессия.Формула n –го члена арифметической прогрессии
А) an =5n-2 Б) bn = 9n + 1 В) cn = 3n - 4 1) 10 2) 13 3) -10 4) -1 Ответ: А- , Б - , В - . Для каждой арифметической прогрессии, заданной формулой ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Историческая справка. Задачи на обе прогрессии встречаются у вавилонян, в египетских папирусах, в древнекитайском трактате «Математика в 9 книгах». ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Введение понятий "больше‒меньше" на числовом луче
1 0 5 меньше левее. 8 больше правее. 3 3 < 5 < 8 8 > 5 > 3. 3 + 5 =. . . ...3 вида разложение многочлена на множители
1 вид вынесение общего множителя за скобки. Что значит разложить многочлен на множители? Разложить многочлен на множители — это значит представить ...Арифметическая и геометрическая прогрессии в заданиях ГИА
Цели урока: Обобщить и систематизировать знания учащихся по данной теме. Разобрать типичные задания встречающихся в сборниках для подготовки к ГИА. ...Арифметическая и геометрическая прогрессии
1. Одна из двух данных последовательностей является арифметической прогрессией, другая – геометрической:. -15; -12; -9; -6; -3; 0;… d=3 32; 16; 8; ...Авария на промышленном объекте
Цели урока:. Повторить материал по темам “ Площади криволинейных трапеций”, “Решение показательных уравнений”, выявить пробелы в знаниях и постараться ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Конспекты
Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Две основные задачи на дроби
. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 8». Методическая разработка урока математики . ...Действия с величинами. Соотношение цены, количества, стоимости. Решение задач, выражений
Автор: Енина Н.В. учитель начальных классов МКОУ НОШ №17 ст.Зольской,. . Ставропольский край. . Урок математики в 3-м классе. УМК «Гармония». ...Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Конспект урока. Учитель: Кононенко Дмитрий Юрьевич. Предмет:. математика. . . Класс 9. Тип урока:. урок изучения нового материала по теме ...Двузначные числа (приём вычисления для случаев вида 36 + 2)
МОУ « СОШ №12 г.Балашова Саратовской области». Урок математики. 1 класс. УМК «Гармония». Двузначные числа. (приём вычисления для случаев ...Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Автор: Сватковская Елена Александровна,. учитель математики,. МБНОУ «Лицей № 3 (искусств)». Арифметическая прогрессия.Формула. n. -го члена ...Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Тема: Арифметическая прогрессия. Формула n. -го члена арифметической прогрессии. Цель:. Совершенствование навыков применения формулы n. -го члена ...Геометрическая прогрессия. Формула n-го члена геометрической прогрессии
Открытый урок в 9 классе МБОУСОШ станицы Терской. Учитель Яшина Н.П. Тема урока: «Геометрическая прогрессия. Формула. n. -го члена геометрической ...Вывод формул для вычисления координат вершины параболы
Нагаева Светлана Николаевна, учитель математики МАОУ « Лицей №1» города Березники. Проект. урока по алгебре в 9 классе. (гуманитарный профиль). ...Действия с обыкновенными дробями. Основные задачи на дроби
ГБС(К)ОУ ШИ. I. -. II. вида г. Тихорецка Краснодарского края. Урок – КВН. в 7 классе по теме:. «Действия с обыкновенными дробями. Основные ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:29 мая 2019
Категория:Математика
Содержит:40 слайд(ов)
Поделись с друзьями:
Скачать презентацию