Презентация "Понятие цилиндра" по математике – проект, доклад
Презентацию на тему "Понятие цилиндра" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 36 слайд(ов).
Слайды презентации
Список похожих презентаций
Понятие функции
Множество х: Все Жильцы.Множество y: номера квартир.
Правило соответствия (зависимости) между множествами : «Каждому жильцу дома будет соответствовать ...
Понятие числа
Основные понятия. Цифра-это знак для обозначения числа Число-понятие, служащие выражением количества. Число состоит из цифр. История возникновения ...Понятие производной
Сегодня у нас праздник! Эпиграф: Был этот мир глубокой тьмой окутан. Да будет свет! И вот явился Ньютон. А.Поуп. Что такое высшая математика? Когда ...Понятие рационального числа
Понятие рационального числа. Рациональные числа - это натуральные, отрицательные и дробные (обыкновенные и конечные десятичные) числа. От английского ...Понятие одночлена стандартный вид одночлена
Определение: Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, ...Понятие площади
реализовать триединые дидактические задачи: через использование различных уровней обучения. обучение, развитие, воспитание. минимальный, базовый, ...Объём цилиндра
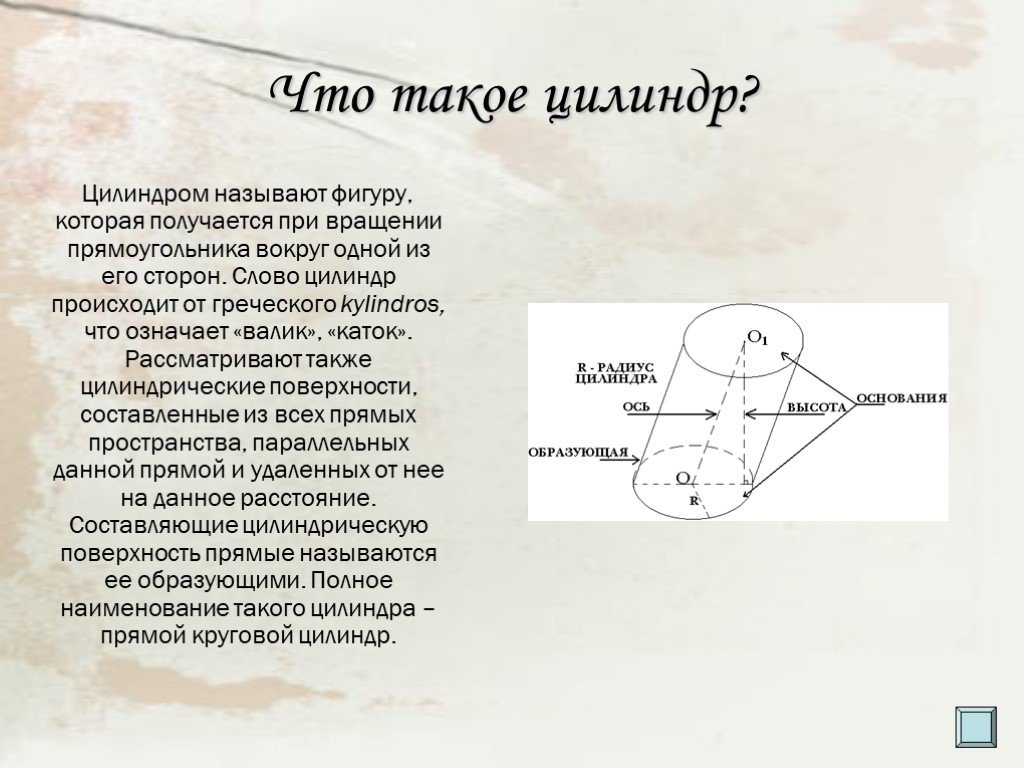
Цилиндр: история. Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …. Цилиндры из жизни. Цилиндры-башни. Водовзводная ...Понятие о производной функции
Цели урока:. ОБУЧАЮЩАЯ : 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический смысл производной; 2) ...Объем цилиндра
Задача. Какое количество нефти вмещает цистерна диаметром 18м. и высотой 7м., если плотность нефти 0,85г/см^3. Определение цилиндра. Тело, ограниченное ...Объем цилиндра
Цилиндр: история. Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …. Цилиндры из жизни. Цилиндры-башни. Водовзводная ...Объём цилиндра
Объём цилиндра равен произведению площади основания на высоту. V=SH=пR^2H. . Решить задачу. Дано: АВ = 26см АС = 12 см Найти: V Решение: V=SH=пR^2H. ...Объем конуса цилиндра
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 300. В ответе укажите . А О 1 Просят найти. Во сколько ...Десятичные дроби. Понятие десятичной дроби
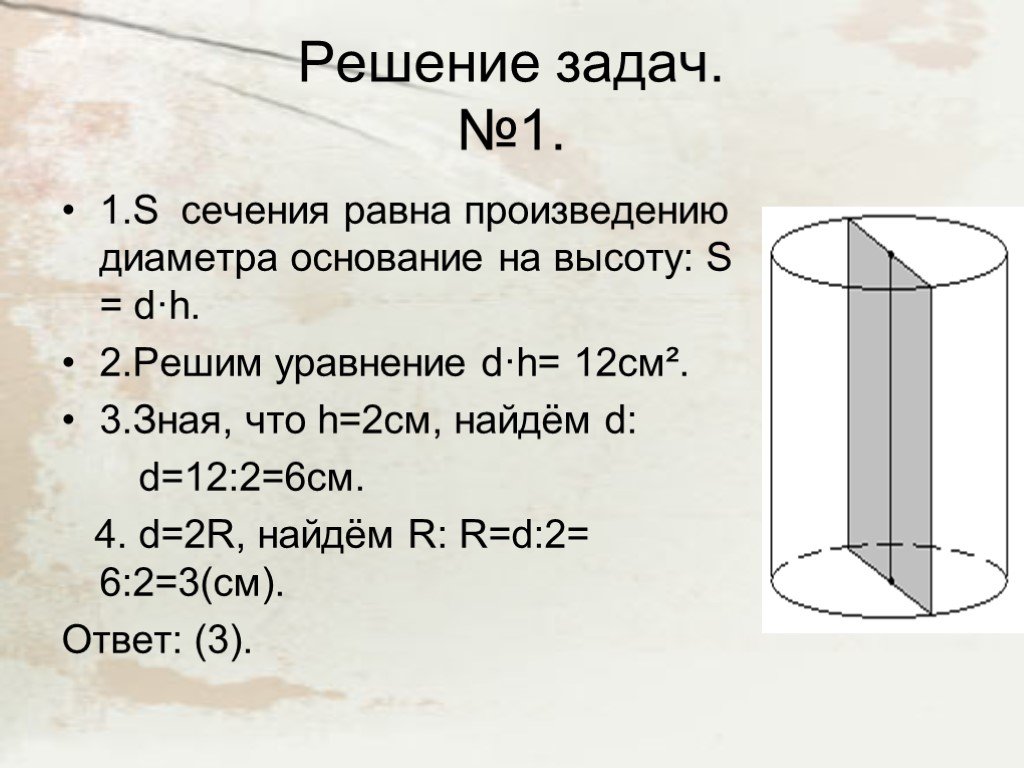
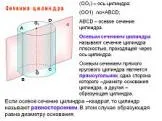
Немного истории. Дроби, как известно, возникли в связи с делением предметов на несколько частей. При решении разных практических задач возникали дроби ...Сечения цилиндра
...Объём цилиндра и конуса
«Не стыдись спросить – не знать еще стыднее!» Японская пословица. В игре участвуют 2 команды. Капитан команды выбирает номер задания, и команда приступает ...Вычисление объёма цилиндра
Устные упражнения по теме. Решение стереометрических задач. Выполнение практической работы. Самостоятельная работа. План урока. Чтобы избегать ошибок, ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Понятие обратной функции. Определение логарифмической функции
Рассмотрим пример какой-либо функции, заданной в явном виде формулой y=f(x). Пусть, для определенности, это будет линейная функция y=2x–7. Вспомним, ...Поверхность цилиндра
Цилиндр- тело ограниченное цилиндрической поверхностью и двумя окружностями, расположенных в параллельных плоскостях, с границами L и L1. Образующие. ...Понятие осевой симметрии
Определение и теорема. Примеры Задачи. Осевой симметрией с осью a называется такое отображение пространства на себя , при котором любая точка М переходит ...Конспекты
Понятие треугольника
Естремская Лидия Ивановна,. . МБОУ Донская СОШ, Орловский район,. учитель математики 1 категории,. Ростовская область. КОНСПЕКТ УРОКА ...Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице
Тема:. Нумерация чисел в пределах 1000. Понятие о сотне как новой счетной единице. 5 класс специальной (коррекционной) школы. Цели:. . . Познакомить ...Понятие процента
Конспект урока по математике в 5 классе. тема урока «Понятие процента». Автор: Кирпина Татьяна Яковлевна, учитель математики МАОУСОШ № 1 г. Окуловка ...Понятие смешанной дроби
ФИО автора: Чемерова Татьяна Владимировна. Место работы:. МБОУ СОШ №3 г. Петровска Саратовской области. Должность:. учитель математики. Предмет:. ...Понятие о системах счисления
Етова Юлия Вячеславовна. Учитель информатики. ГБОУ Центр Образования №1469, город Москва. Понятие о системах счисления. ...Понятие об обыкновенной дроби
Тема: Понятие об обыкновенной дроби. Цели:. Познакомить учащихся с основными понятиями: обыкновенная дробь, числитель дроби, знаменатель дроби; ...Понятие вектора
Муниципальное общеобразовательное учреждение. «Завьяловская средняя общеобразовательная школа №1». Завьяловского района Алтайского края. ...Понятие о производной функции. Ее геометрический и физический смысл
Дата. . Класс. . Предмет. . . 14.11.2013. . . 11. . Алгебра и начала анализа. . . . Тема урока:. Понятие о производной ...Понятие арккосинуса. Уравнение вида сosх = а
Разработчик материала:. . Матвеева Мария Викторовна. учитель математики. ГБОУ ШИ «Олимпийский резерв». Программированный урок для 10 класса ...Понятие вектора
Учитель математики - Юшина Раиса Алексеевна. . МБОУ СОШ № 18. . . Тема:. 9КЛ. . 2010. год. Тема:. Понятие ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 марта 2019
Категория:Математика
Содержит:36 слайд(ов)
Поделись с друзьями:
Скачать презентацию