Презентация "Объем цилиндра" по математике – проект, доклад
Презентацию на тему "Объем цилиндра" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 19 слайд(ов).
Слайды презентации
Список похожих презентаций
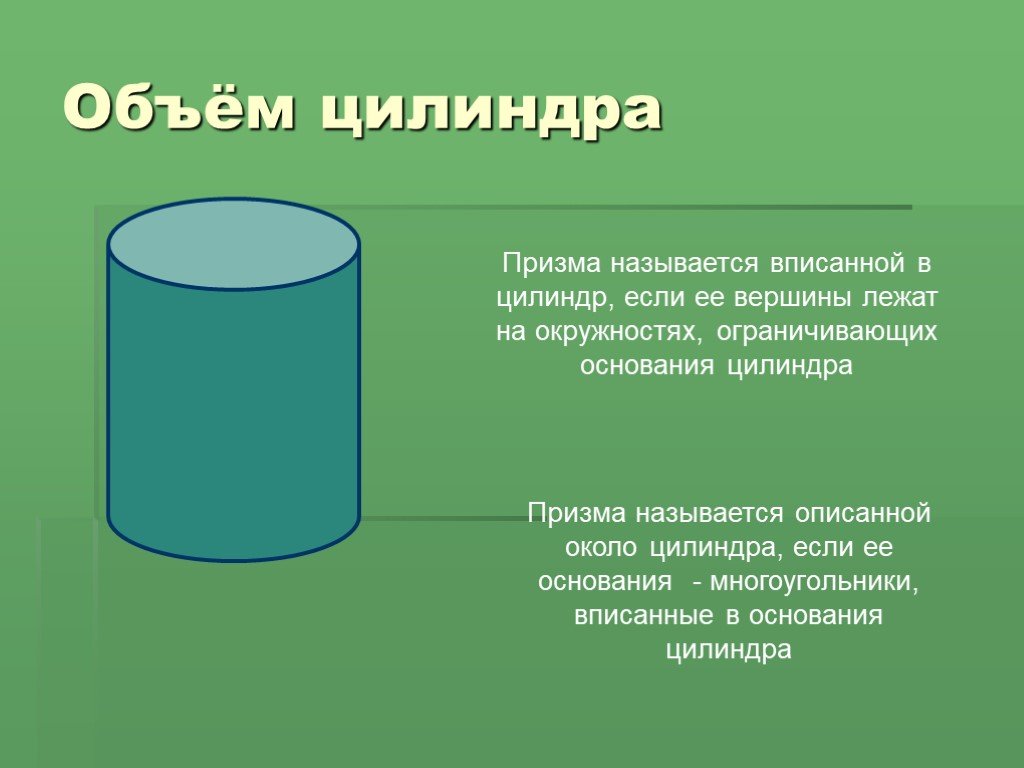
Объем цилиндра
Задача. Какое количество нефти вмещает цистерна диаметром 18м. и высотой 7м., если плотность нефти 0,85г/см^3. Определение цилиндра. Тело, ограниченное ...Объем конуса цилиндра
Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 300. В ответе укажите . А О 1 Просят найти. Во сколько ...Объем конуса
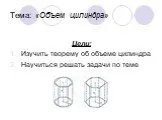
План урока:. Организационный момент. Повторение основных сведений о конусе. Историческая справка. Объяснение нового материала. Решение задач на объем ...Сечения цилиндра
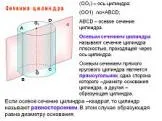
...Сечения конуса и цилиндра
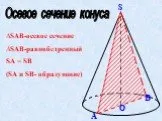
M N. Сечение конуса плоскостью, проходящей через его вершину. ∆SMN-равнобедренный SM=SN - образующие. Дуга NM = φ, значит φ K α. Осевое сечение O1 ...Понятие объема многогранников. Объем прямоугольного параллелепипеда
1. О понятие объема тела. Аналогия с S M S(M) Равные многоугольники имеют равные площади. Площадь многоугольника равна сумме площадей составляющих ...Объемы. Объем прямоугольного параллелепипеда
1 = ? 4·16 +11 :15 ·12 -20. 2 19·3 -9 :12 ·25 :10. 3. Соревнование с первоклассником Корова-2,овца-2,свинья-3,собака-3,кукушка-4,лошадь-5,петух-8. ...Объём цилиндра и конуса задачи практического содержания
№ 1 1 вариант. Выполните рисунок цилиндра, обозначьте на рисунке радиус, высоту. 2 вариант. Выполните рисунок конуса, обозначьте на рисунке образующую, ...Объём цилиндра
Цилиндр: история. Слово "цилиндр" происходит от греческого kylindros, что означает "валик", "каток " …. Цилиндры из жизни. Цилиндры-башни. Водовзводная ...Объем призмы
Ход урока:. Вступительное слово учителя Повторение материала проводится в форме игры «Поле чудес Правила игры: выбор троек игроков после правильного ...Объем пирамиды
Определение. Пирамидой называется многогранник, одна грань которого – произвольный многоугольник, а остальные грани – треугольники, имеющие общую ...Объем пирамиды
Необходимые формулы и теоремы. Площадь треугольника можно вычислить по формулам Площадь прямоугольного треугольника можно вычислить по формуле Объем ...Объем параллелепипеда
Объем куба. Объем куба с ребром а вычисляется по формуле. а. Объем прямоугольного параллелепипеда вычисляется по формуле. Объем любого параллелепипеда ...Объем конуса
Работу выполнили Ученицы 11 класса МОУ «Тугустемирская СОШ» Кудряшова Наташа Дусаева Гульнара. Теорема. Объем конуса равен одной трети произведения ...Объём цилиндра
Объём цилиндра равен произведению площади основания на высоту. V=SH=пR^2H. . Решить задачу. Дано: АВ = 26см АС = 12 см Найти: V Решение: V=SH=пR^2H. ...Объем прямой призмы
Теорема: объем прямой призмы равен произведению площади основания на высоту. Доказательство. 1. Рассмотрим прямую треугольную призму АВСА1В1С1 С ОБЪЕМОМ ...Объем прямой призмы
Цели урока:. Вспомнить понятие призмы. Изучить теорему об объеме призмы. Провести доказательство. Применить полученные знания на практике. Призма ...Объём цилиндра и конуса
«Не стыдись спросить – не знать еще стыднее!» Японская пословица. В игре участвуют 2 команды. Капитан команды выбирает номер задания, и команда приступает ...Объем прямоугольного параллелепипеда
ПЛОСКИЕ ОБЪЕМНЫЕ ФИГУРЫ. ПЛОСКИЕ ФИГУРЫ. ТРЕУГОЛЬНИК КВАДРАТ ПРЯМОУГОЛЬНИК КРУГ ЧЕТЫРЕХУГОЛЬНИК. КУБ ЦИЛИНДР ПАРАЛЛЕПИПЕД. ОБЪЕМНЫЕ ФИГУРЫ. Планиметрия ...Объем шара. Площадь сферы
Внешний диаметр полого шара равен 18 см, а толщина стенок - 3 см. Найдите объем материала, из которого сделан шар. №1. Внутренний диаметр полого шара ...Конспекты
Объемы цилиндра конуса
Объемы цилиндра конуса. Цель: совершенствовать навыки решения задач на нахождение объемов фигур. . вращения (цилиндра и конуса). Задачи: -способствовать ...Прямоугольный параллелепипед. Объем прямоугольного параллелепипеда
Технологическая карта урока. Разработчик. : учитель математики ГБОУ СОШ с. Криволучье-Ивановка. Самарской обл., Красноармейского р-она Баранов ...Площадь боковой поверхности цилиндра и конуса
Конспект урока по математике. Данные о преподавателе:. Кочерягина Галина Владимировна,. I. квалификационная категория,. . государственное ...Площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра. . . . . равна . , а диаметр основания — 8. Найдите высоту цилиндра. . Длина окружности основания ...Объемы. Объем прямоугольного параллелепипеда
Урок математики в 5 классе. . . Тема:. Объемы. Объем прямоугольного параллелепипеда. Цель:. 1. Закрепить знания по данной теме при решении задач. ...Объем шара
. Урок геометрии в 11 классе. . Тема урока:. Объем шара. Учитель: Кусекеева Г.Б. Дата:. . Цели урока:. образовательные:. обобщить и систематизировать ...Объем прямоугольного параллелепипеда
Предмет — математика. . Класс: 5. Тема урока:. Объем прямоугольного параллелепипеда. Главная дидактическая цель:. закрепление навыков. ...Объем прямоугольного параллелепипеда
Осмоловская Нина Федоровна. учитель математики. Муниципального общеобразовательного учреждения Усвятская средняя общеобразовательная школа Дорогобужского ...Объем пирамиды
Коспект урока по геометрии в 11 классе «Объем пирамиды». Цели занятия:. 1. . Образовательные:. • ознакомление учащихся с геометрическим телом – ...Объем наклонного параллелепипеда. Объем призмы
Технологическая карта. Класс – 11. Предмет – геометрия. Тема - Объем наклонного параллелепипеда. Объем призмы. Проверка домашнего задания. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:25 марта 2019
Категория:Математика
Содержит:19 слайд(ов)
Поделись с друзьями:
Скачать презентацию









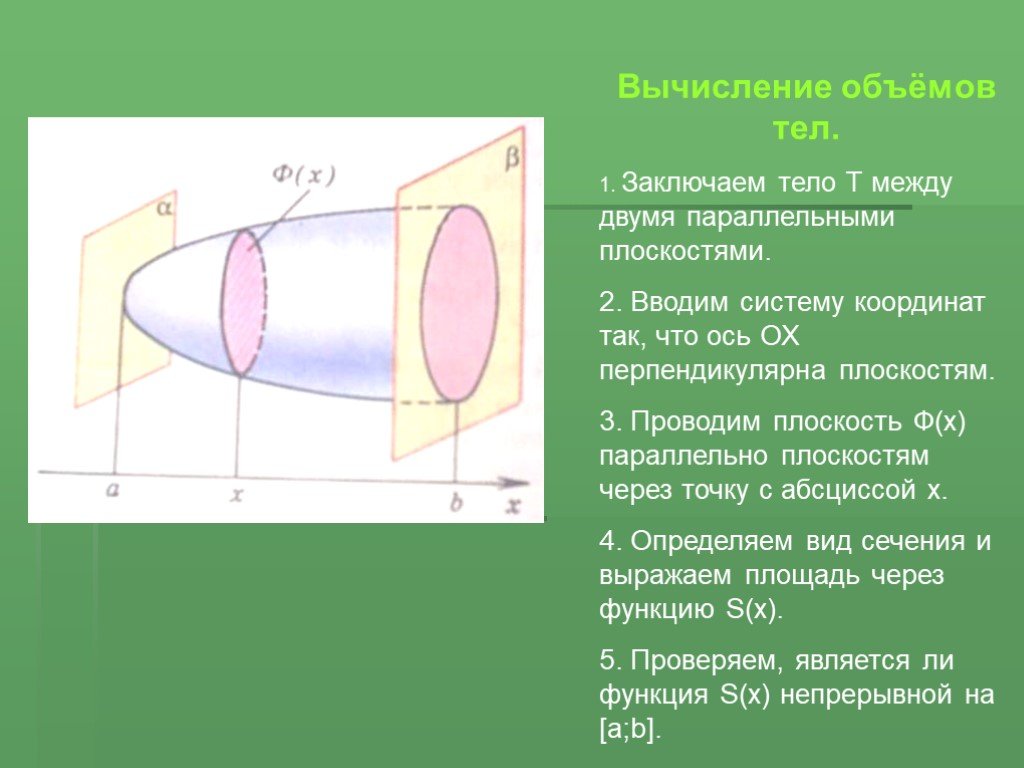


















![6. Разбиваем [a;b] на n - равных отрезков точками а = х0, х1, х2, …хn=b и проводим через хi плоскости перпендикулярно ОХ. 7. Плоскости разбивают тело Т на n- тел Т1, Т2, Т3,... Тn с основаниями Ф(хi) и высотой xi = (b - a)/n. 8. V Vn= (S(x1) + S(x2) +…+ S (xn) )xi = (S(x1) + S(x2) +… + S (xn))(b 6. Разбиваем [a;b] на n - равных отрезков точками а = х0, х1, х2, …хn=b и проводим через хi плоскости перпендикулярно ОХ. 7. Плоскости разбивают тело Т на n- тел Т1, Т2, Т3,... Тn с основаниями Ф(хi) и высотой xi = (b - a)/n. 8. V Vn= (S(x1) + S(x2) +…+ S (xn) )xi = (S(x1) + S(x2) +… + S (xn))(b](https://prezentacii.org/upload/cloud/19/03/136476/images/thumbs/screen15.jpg)