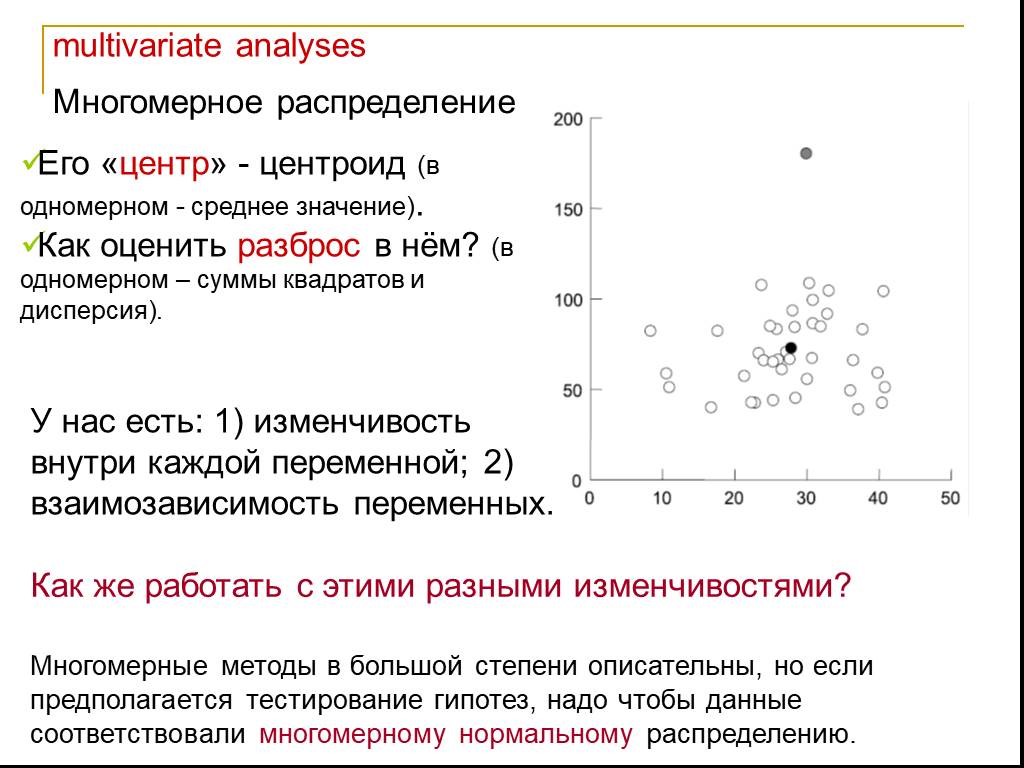
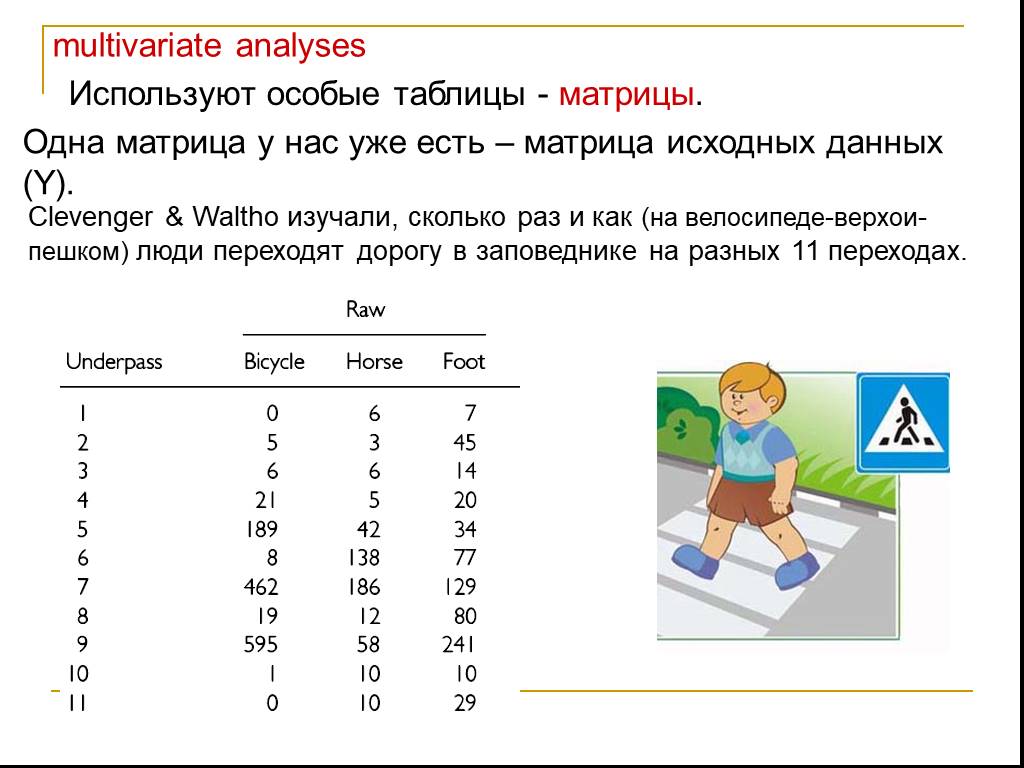
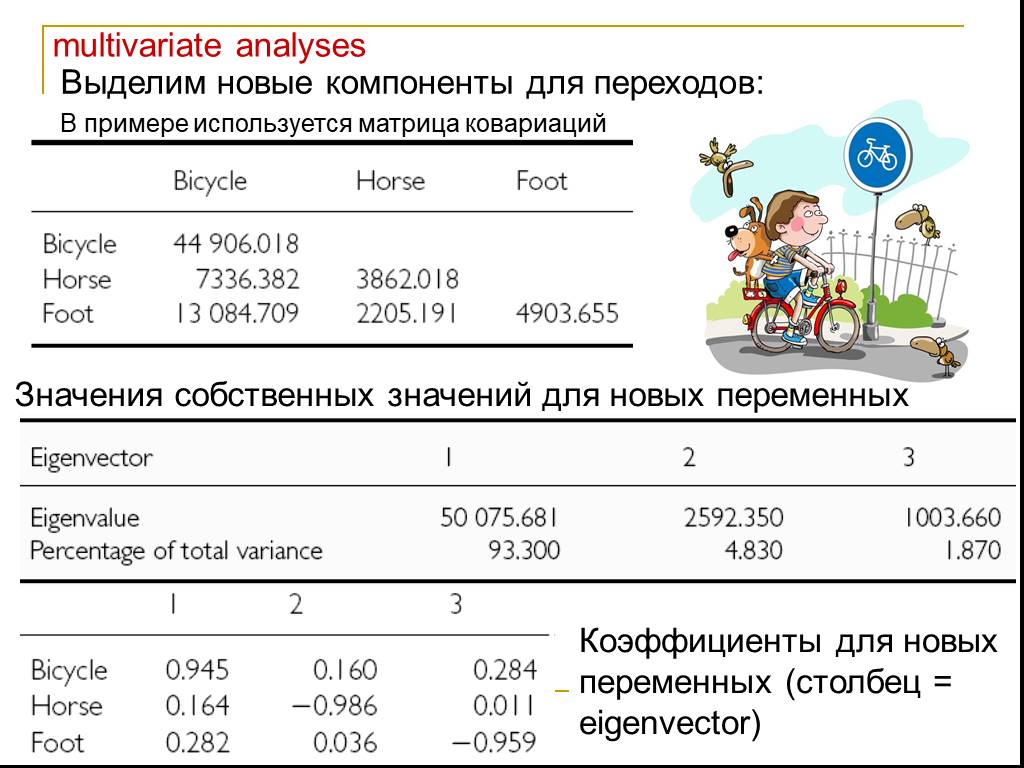
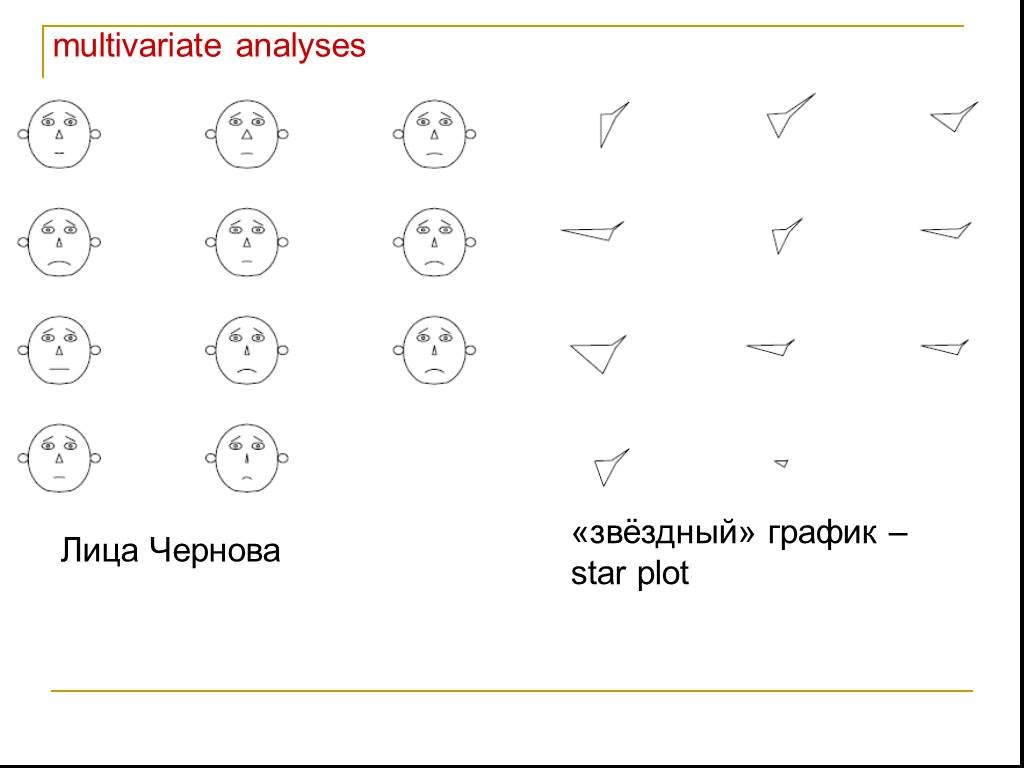
Презентация "Основы многомерных методов анализа. Факторный анализ" по математике – проект, доклад
Презентацию на тему "Основы многомерных методов анализа. Факторный анализ" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 39 слайд(ов).
Слайды презентации
Список похожих презентаций
Основы концепции “глубинного анализа текстов
Контент-анализ: определения. Один из истоков концепции Text Mining – контент-анализ. Понятие контент-анализа, корни которого в психологии и социологии, ...Алгебра и начала математического анализа
УМК "Алгебра и начала анализа" 10 – 11 класс. Профильный уровень. ЦЕЛЬ: Оказать методическую помощь учителям при выборе УМК для работы в профильных ...Урок алгебры и начал анализа
. Эпиграф:. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство ...Алгебра и начала анализа "Логарифмическая функция"
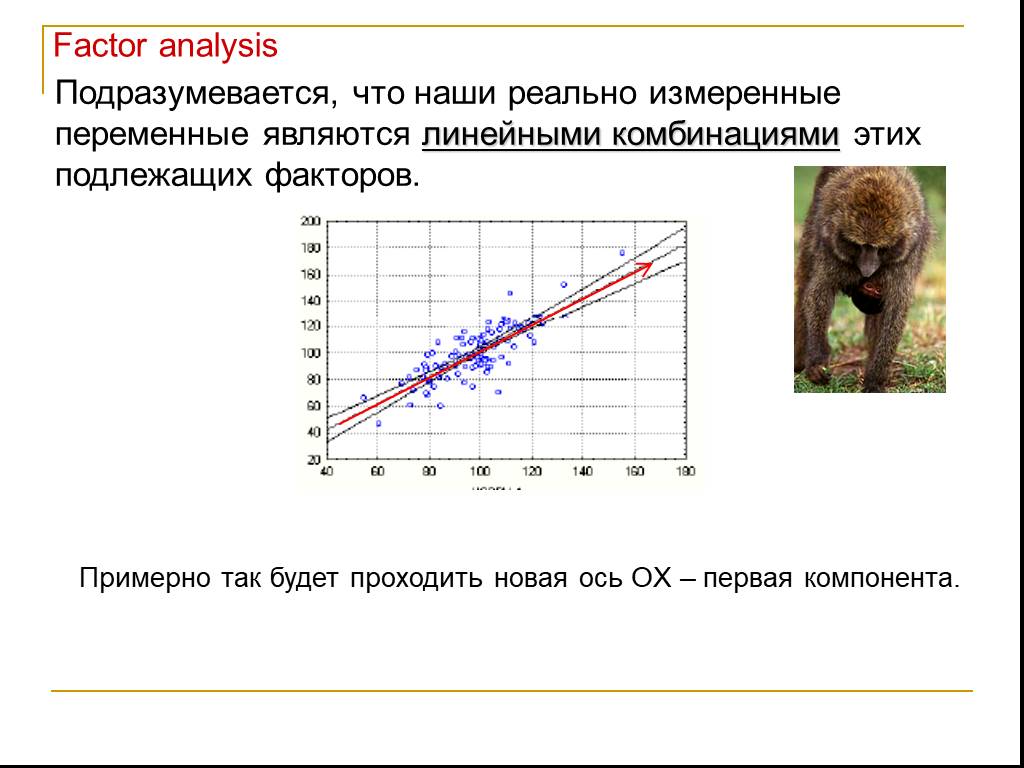
Содержание. Титульный лист Содержание Определение логарифмической функции Свойства логарифмической функции График логарифмической функции Примеры. ...Факторный анализ
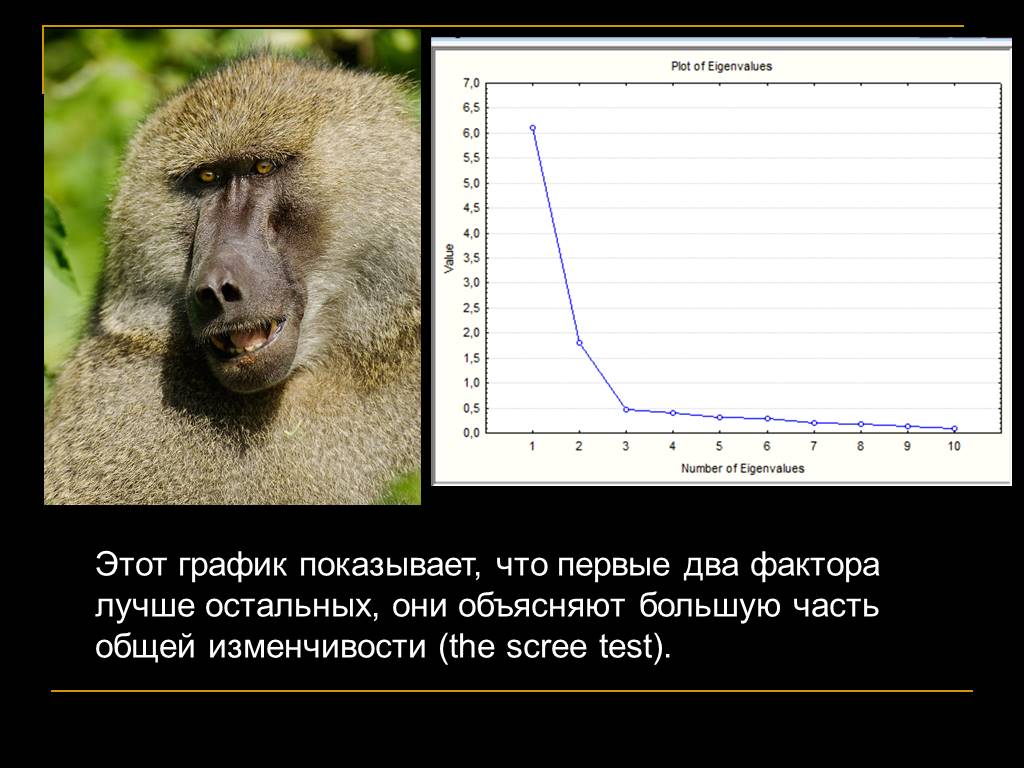
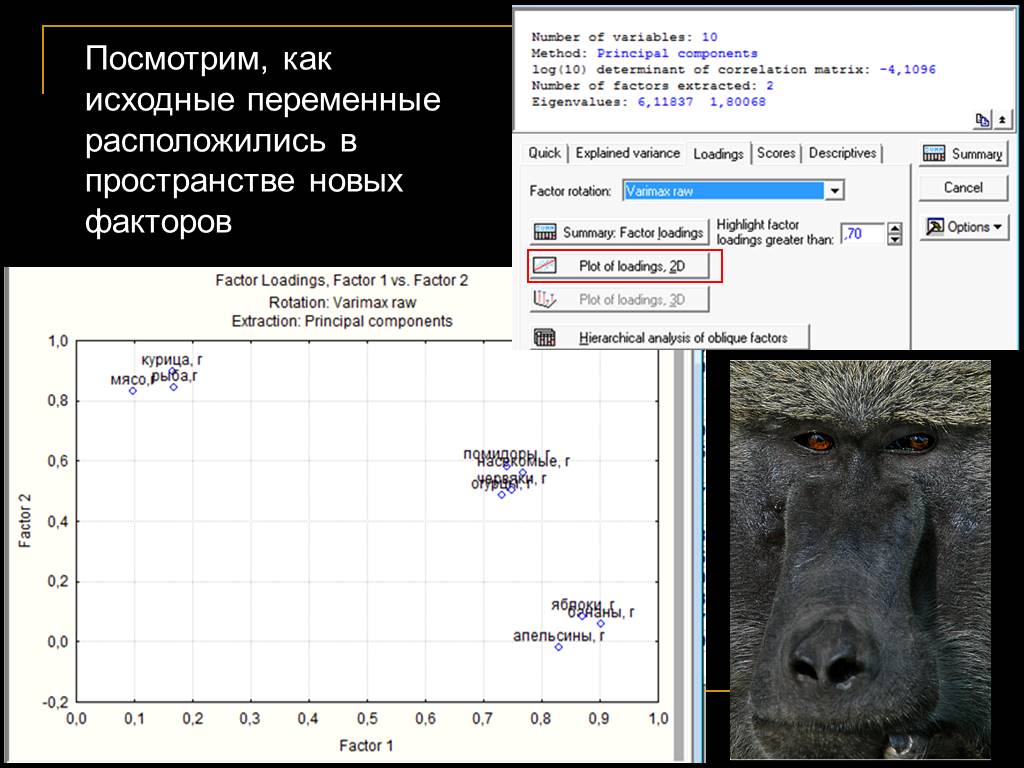
Термин факторный анализ впервые ввел Thurstone, 1931 Факторный анализ в современной статистике - совокупность методов, которые на основе реально существующих ...Открытый урок по алгебре и началам анализа
Урок- семинар. Цель: Обобщить знания учащихся по данной теме, продемонстрировать различные методы решения иррациональных уравнений, показать умение ...Применение элементов математического анализа при решении задач
- Учиться проводить анализ условия задачи, что помогает поиску способа решения;. Цели урока. - Учиться переводить язык задачи на язык производной ...Алгебра и начала анализа 10-11 класс
Числовые функции, заданные формулами y=sin x и y=cos x,называют соответственно - ??? и ???. Числовые функции, заданные формулами y=tg x и y=ctg x, ...Использование схемы анализа на уроках математики и литературы
Буква и цифра, Слово и число, Словесность и математика… - две формы общения человека с миром. Слово – Бог… Математика – Королева наук… Так ли они ...Задания на построение и анализ функций
Задания на построение и анализ функций. А это наша комиссия. Районный эксперт по математике. Директор и завуч. Математик Васильева Маргарита Викторовна. ...Основы тригонометрии
Этапы развития тригонометрии. Тригонометрия в древности являлась вспомогательным разделом астрономии. Древнегреческие ученые разработали «тригонометрию ...Основы теории вероятности
Основные понятия теории вероятностей. Событием называется любой исход опыта, различают следующие виды событий: - случайные - достоверные - невозможные ...Основы логики. Алгебра высказываний
Логика. Логика – это наука о формах и способах мышления, позволяющая строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. ...Основы логики
Комбинаторика Классификация Сравнение Анализ Синтез. КОМБИНАТОРИКА –. перебор возможных вариантов. Из цифр 1, 2, 3 составить возможные двузначные ...Детерминационный анализ
Это система методов анализа социологических и социально-экономических данных, в которой задачи обработки и интерпретации ставятся как задачи анализа ...Основы комбинаторики
Правило произведения Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными ...Дисперсионный анализ
Основной целью дисперсионного анализа является исследование значимости различия между средними. Установить различаются ли три группы или более по ...Задача и пять методов её решения
Введение. Для успешного изучения геометрии необходимо знать не только основные формулы и теоремы, но и владеть различными методами решения задач. ...Применение вероятностных методов
Применение теории вероятности. Что такое вероятность? «Вероятность – возможность исполнения, осуществимости чего-нибудь». Какое определение дает основатель ...Множественный регрессионный анализ
Построение уравнения регрессии 1. Постановка задачи. Данные наблюдений. По имеющимся данным n наблюдений за совместным изменением параметров y, xj ...Конспекты
Алгебра и начала анализа 10 класс
Алгебра и начала анализа 10 класс(поурочные планы). . 1-е полугодие. . Глава 1. Числовые функции. . Уроки 1-2. Определение числовой функции ...Применение графических и геометрических методов при решении текстовых задач
Тема урока. : Применение графических и геометрических методов при решении текстовых задач. (11 класс). Цели. :. Обучающая:. научить решать текстовые ...Основы тригонометрии
Учитель математики первой категории Славкина Надежда Владимировна ОСШ №39 имени М.Жумабаева города Шымкента,. . Южно-Казахстанской области. ...Использование математических методов исследования при изучении физики
. Севастопольская билингвальная гимназия № 2 СГС. Бинарный урок физики и математики. на французском языке. « Использование ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 марта 2019
Категория:Математика
Содержит:39 слайд(ов)
Поделись с друзьями:
Скачать презентацию