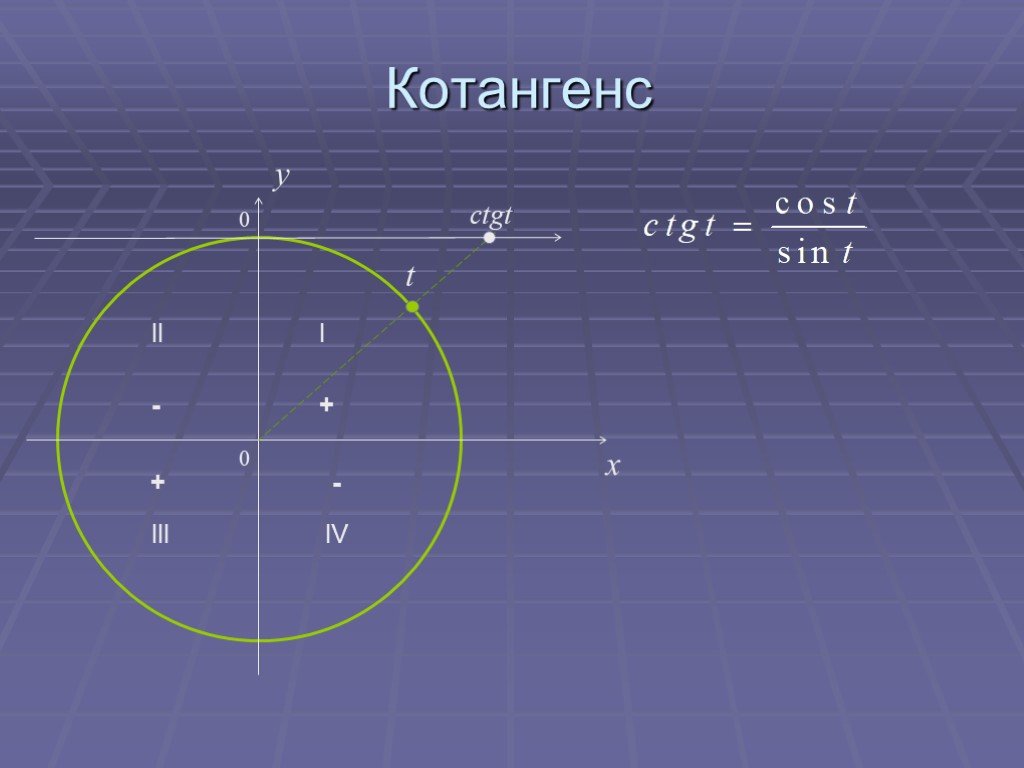
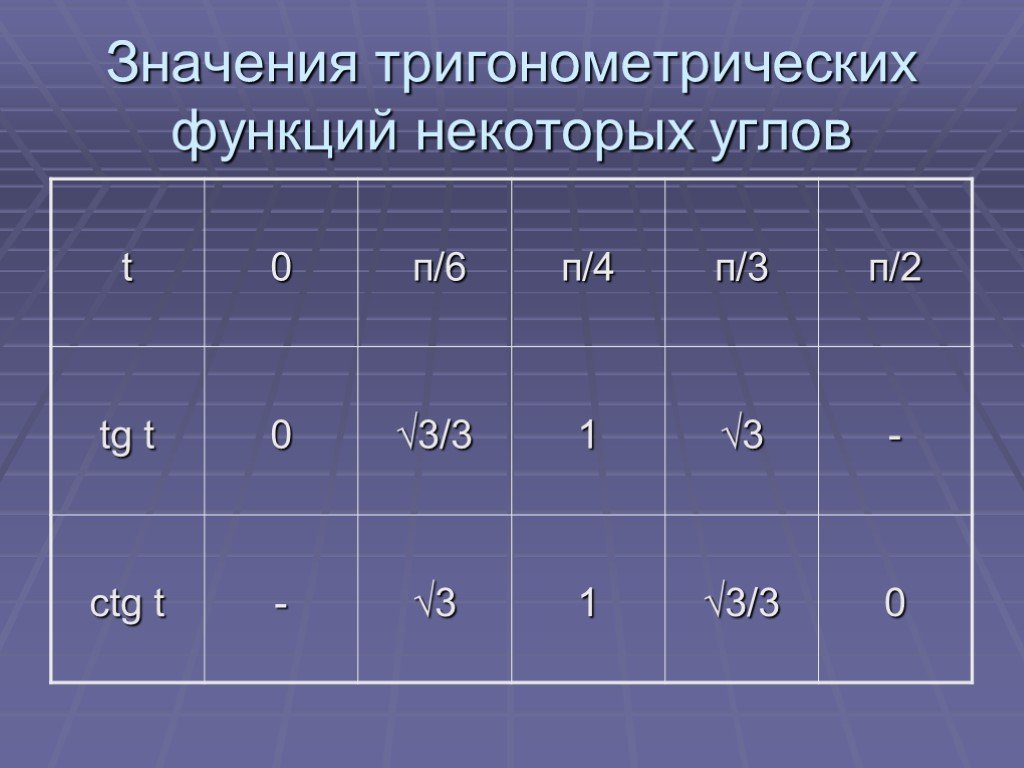
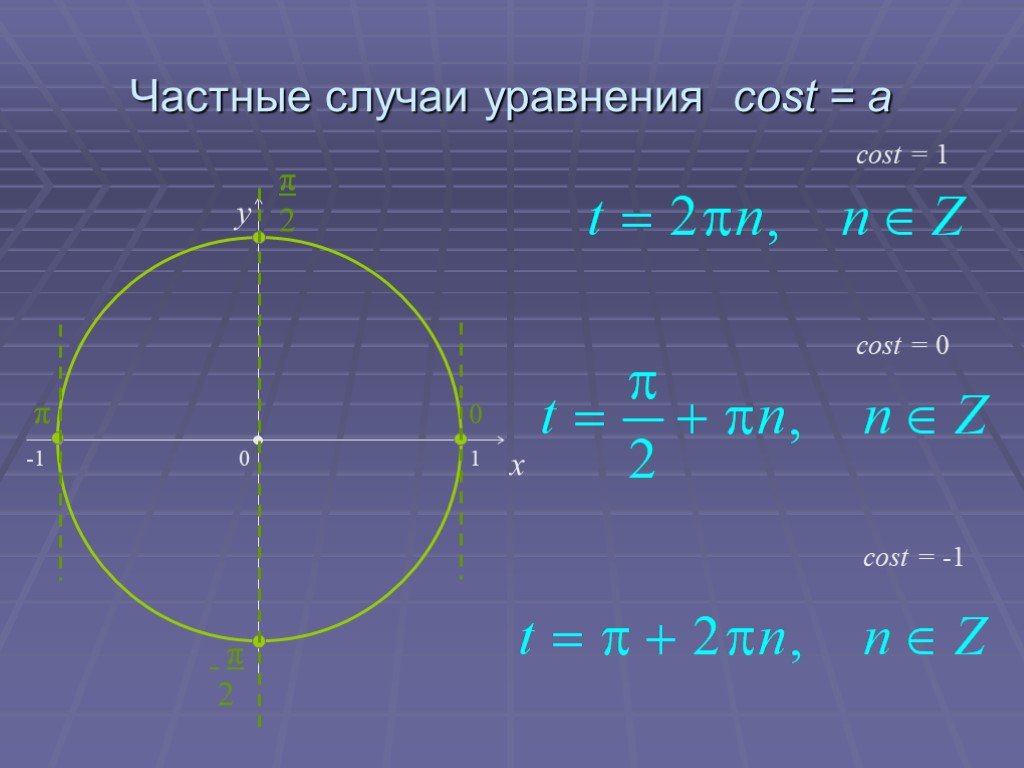
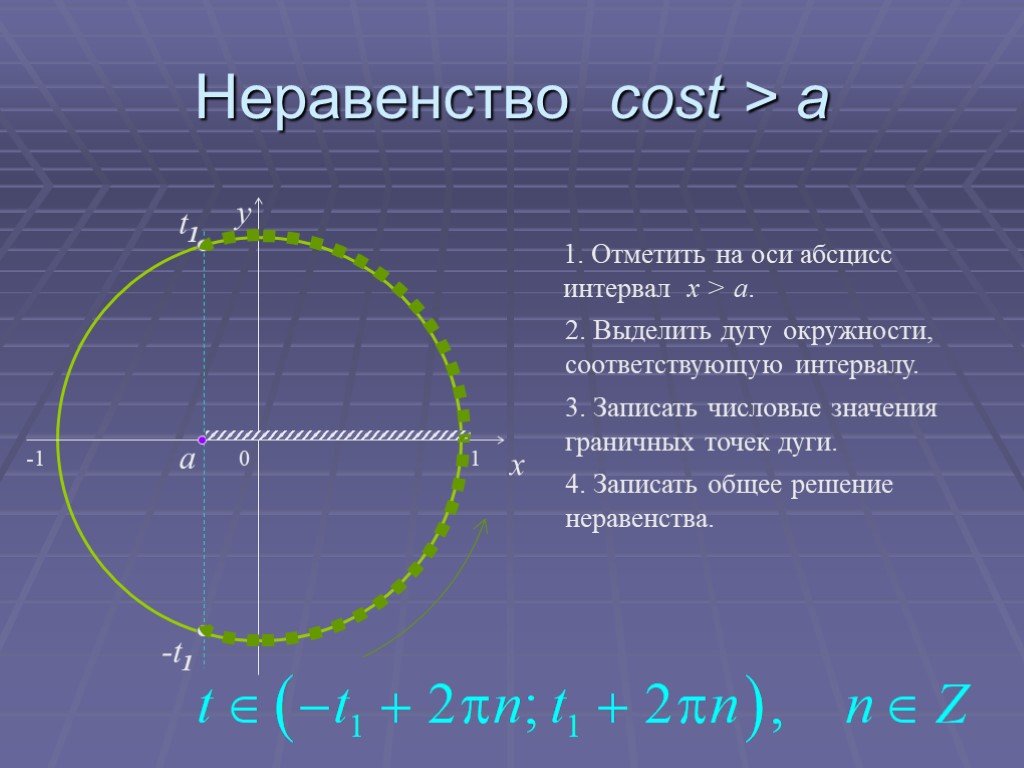
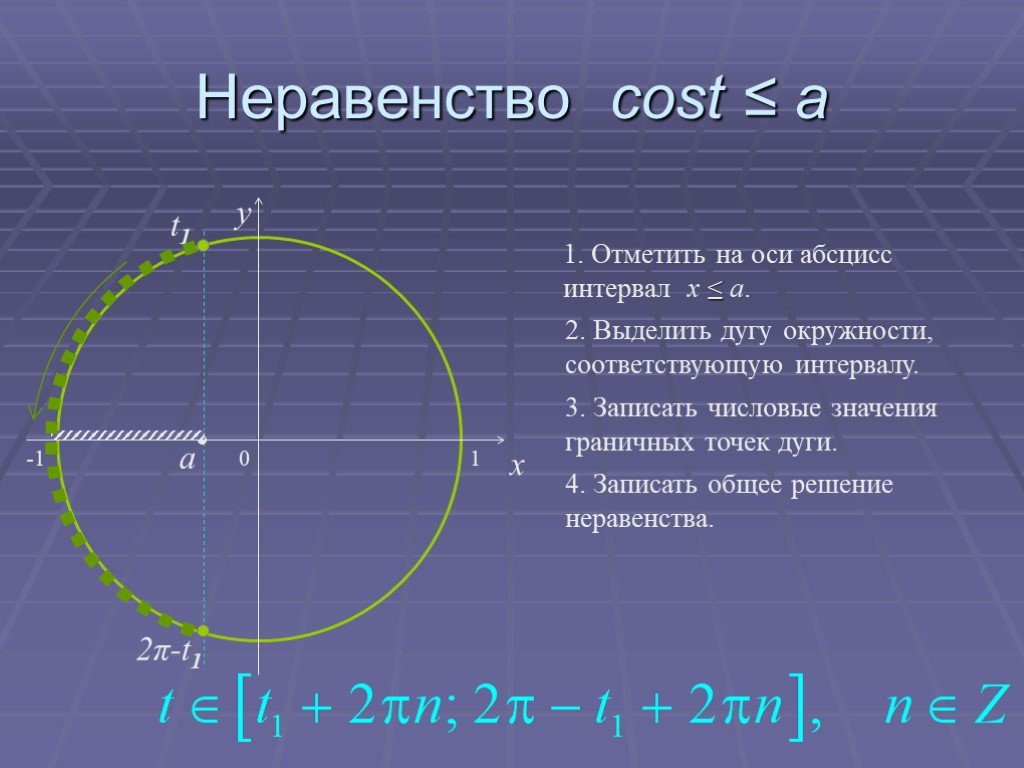
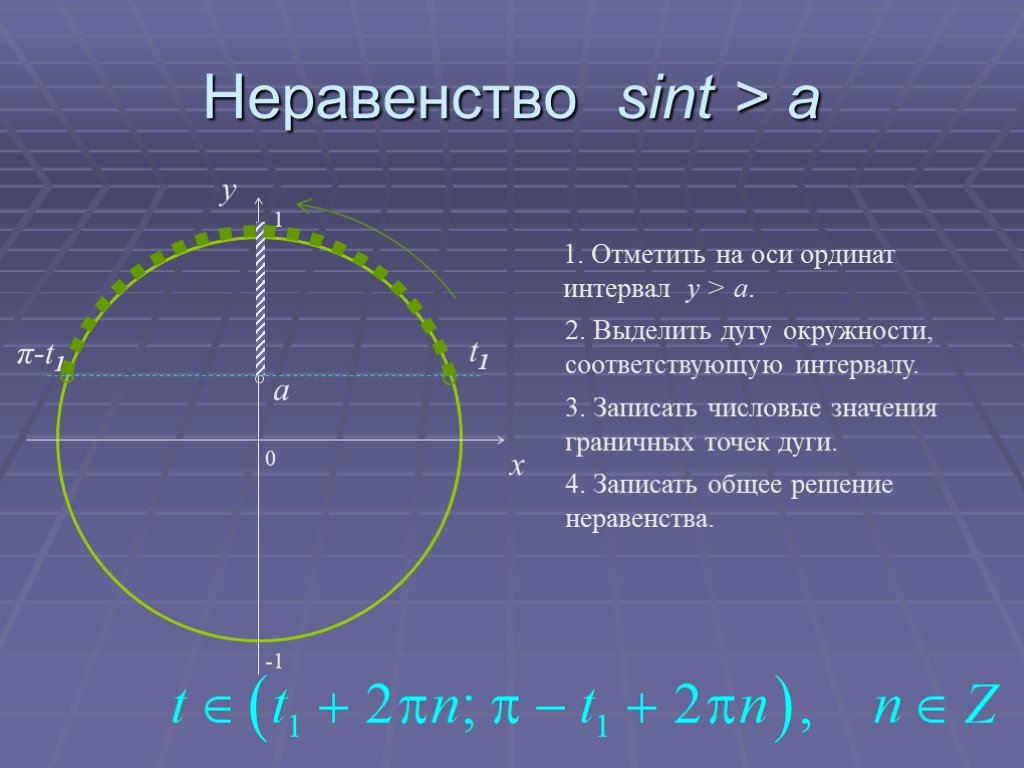
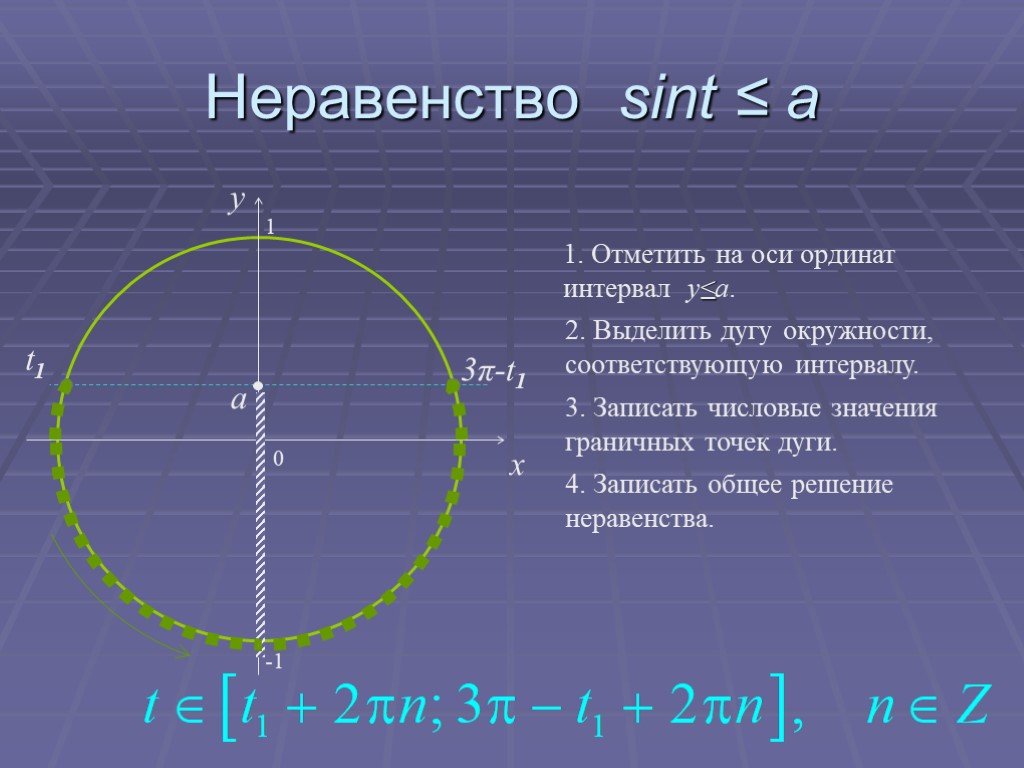
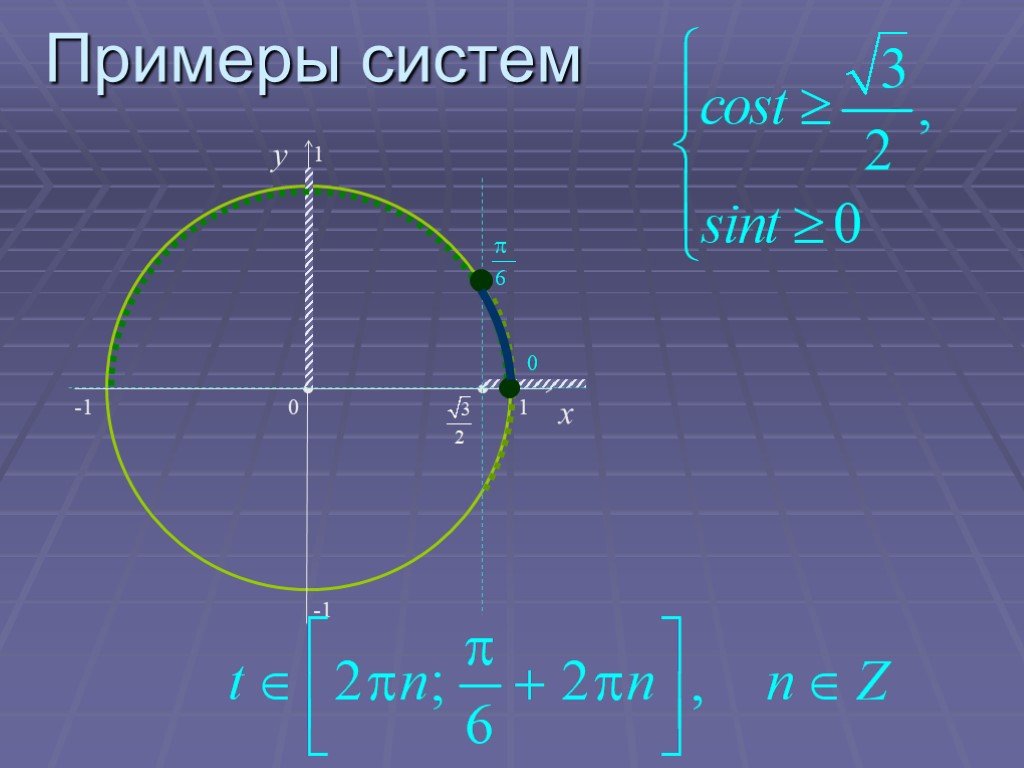
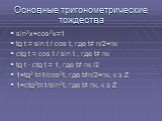
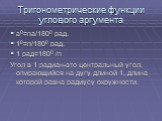
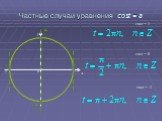
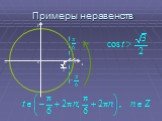
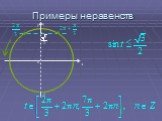
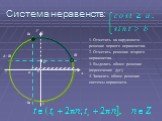
Презентация "Основы тригонометрии" по математике – проект, доклад
Презентацию на тему "Основы тригонометрии" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Основы многомерных методов анализа. Факторный анализ
Методы многомерного анализа (multivariate analyses) Предназначены для анализа многомерных данных. Много независимых переменных – Многофакторная ANOVA ...Основы теории вероятности
Основные понятия теории вероятностей. Событием называется любой исход опыта, различают следующие виды событий: - случайные - достоверные - невозможные ...Основы логики
Комбинаторика Классификация Сравнение Анализ Синтез. КОМБИНАТОРИКА –. перебор возможных вариантов. Из цифр 1, 2, 3 составить возможные двузначные ...Основы логики. Алгебра высказываний
Логика. Логика – это наука о формах и способах мышления, позволяющая строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. ...Основы комбинаторики
Правило произведения Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными ...Основы концепции “глубинного анализа текстов
Контент-анализ: определения. Один из истоков концепции Text Mining – контент-анализ. Понятие контент-анализа, корни которого в психологии и социологии, ...Основы высшей математики и математической статистики
Учебники:. Н.Л. Лобоцкая и др. Высшая математика. Мн.1987г. Морозов Ю.В. Основы высшей математики и статистики. М. 1998г. И.В. Павлушков и соавт. ...Элементы тригонометрии
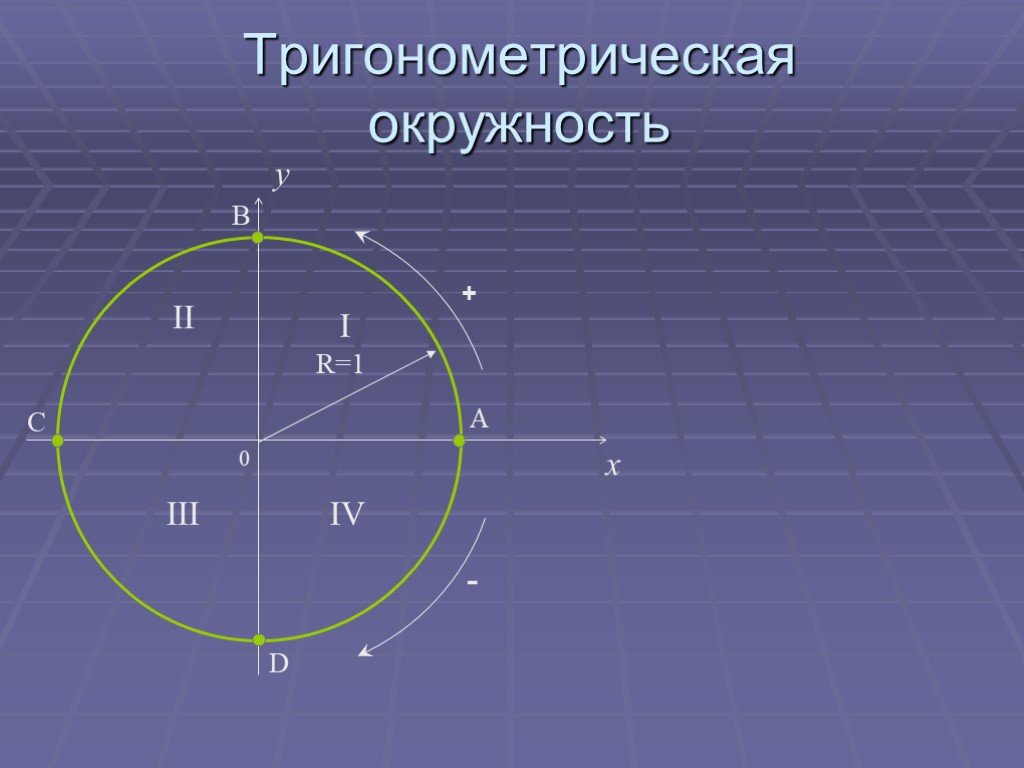
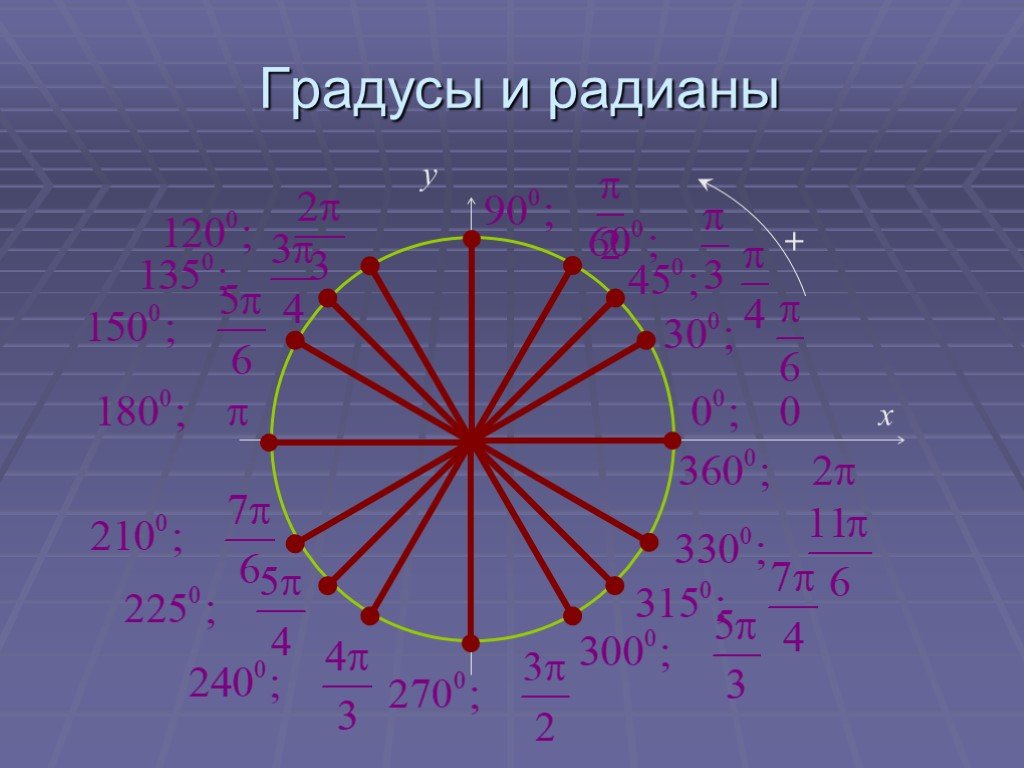
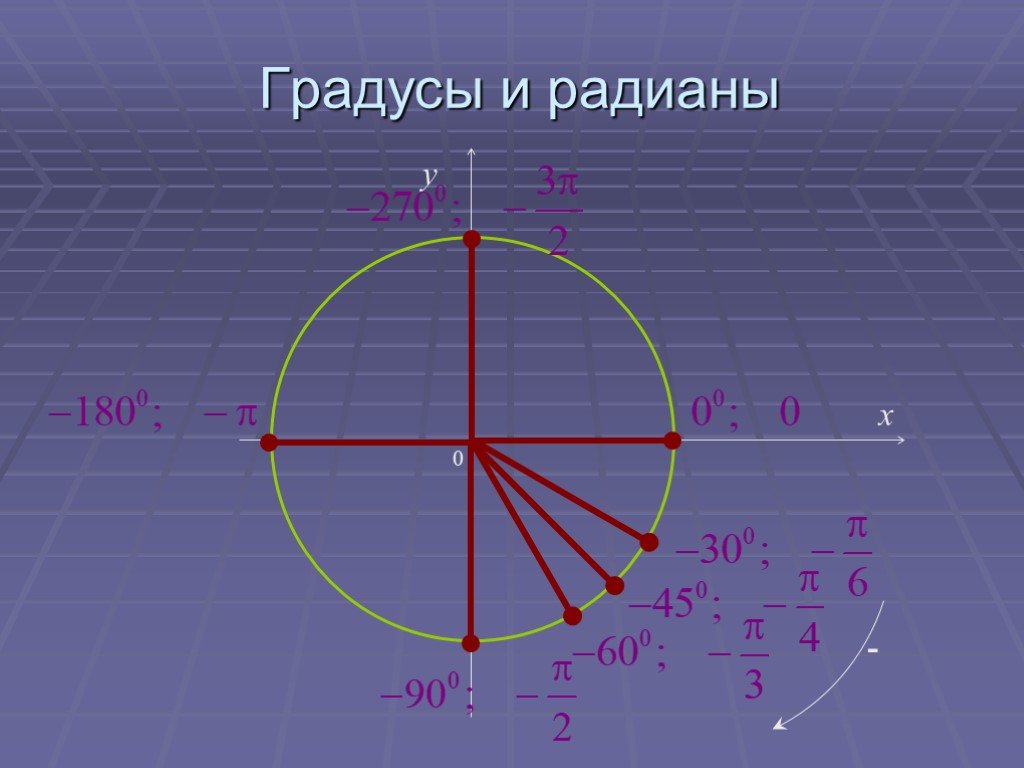
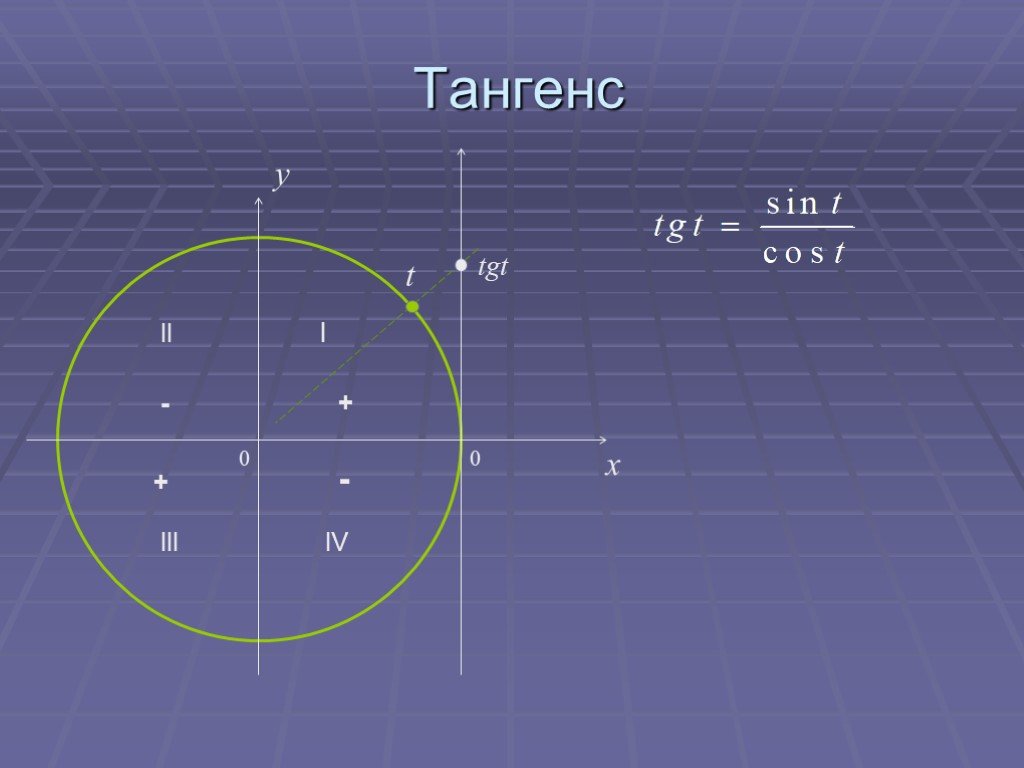
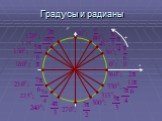
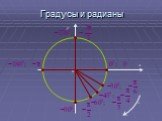
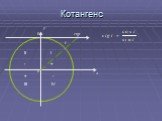
На тригонометрическом круге:. определения синуса, косинуса, тангенса и котангенса угла; радианное измерение углов; область определения и область значений ...Основные формулы тригонометрии
Содержание. Из истории… 2) Основные тригонометрические формулы а) основные тригонометрические тождества б) формулы сложения в) формулы суммы и разности ...Основы бизнес-математики
Дидактическая цель: Представить учащимся краткий исторический очерк развития рынка; Показать, что математические величины и зависимости – отображение ...Основные формулы тригонометрии
Могут ли одновременно выполняться равенства? Правильный ответ: Да 17.06.2019. . Нет. Вычислите:. учитель математики Кустова М.О. . - 0,6. . . . . ...История тригонометрии
Содержание. Определения История Синус, косинус, тангенс Дальнейшее развитие Аналитическая теория Список литературы. Определения. Тригономе́трия-от ...История тригонометрии
Издавна установилась такая практика, что при систематическом обучении математике ученику приходится встречаться с тригонометрией трижды. Соответственно ...История развития тригонометрии
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса. Тригонометрия – слово греческое и в буквальном ...Основы геометрического практикума при изучении математики
ОКР.(О;3СМ.5ММ). Мы начертили окружность с центром в точке О и радиусом 3 см 5 мм, провели прямую, которая пересекает окружность в точке М и К. о ...Уравнения в тригонометрии
Цели урока. Образовательные: обобщить знания по теме «Решение простейших тригонометрических уравнений», проверить практические навыки и умения учащихся ...Решение задач по механике с использованием тригонометрии
Наука начинается тогда, когда начинают считать. Д.И.Менделеев. Слеп физик без математики. М.В.Ломоносов. Рано или поздно всякая правильная математическая ...Задания по тригонометрии
Достроить проекции плоского пятиугольника АВСДЕ , если: заданы АВ и ВС и фронтальная проекция АЕ; ВС параллельно П1; ЕД параллельна П2; /ВС/ =/ЕД/. ...Синус, косинус, тангенс и котангенс, алгебра,
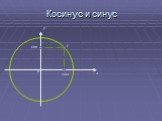
Синус и косинус. Что будем изучать:. Определение синуса и косинуса. Определение тангенса и котангенса. Основное тригонометрическое тождество. Примеры ...Тригонометрические функции углового аргумента - алгебра,
Тригонометрическая функция углового аргумента. Что будем изучать:. Определение. Примеры. Вспомним геометрию. Градусная мера угла. Радианная мера угла. ...Конспекты
Основы тригонометрии
Учитель математики первой категории Славкина Надежда Владимировна ОСШ №39 имени М.Жумабаева города Шымкента,. . Южно-Казахстанской области. ...Решение задач по механике с использованием тригонометрии
Муниципальное общеобразовательное учреждение. Средняя общеобразовательная школа № 34 города Томска. Конспект интегрированного урока ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:24 октября 2018
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию