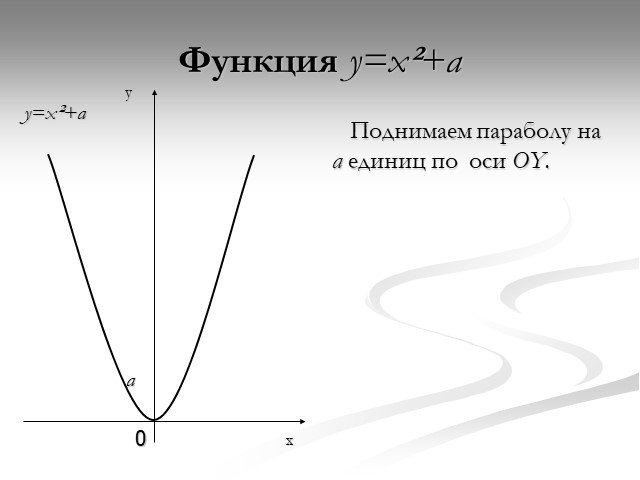
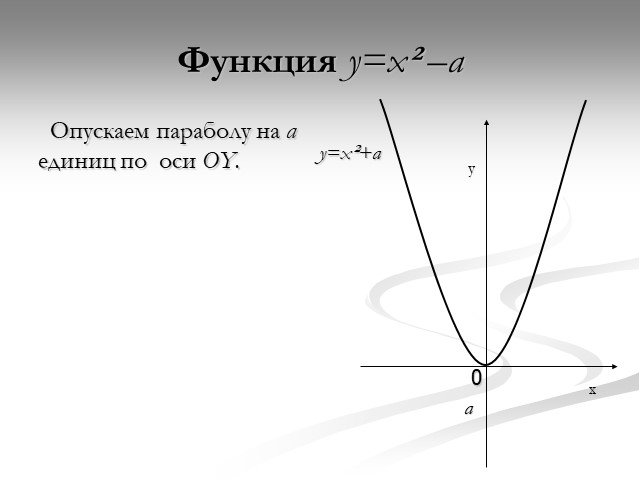
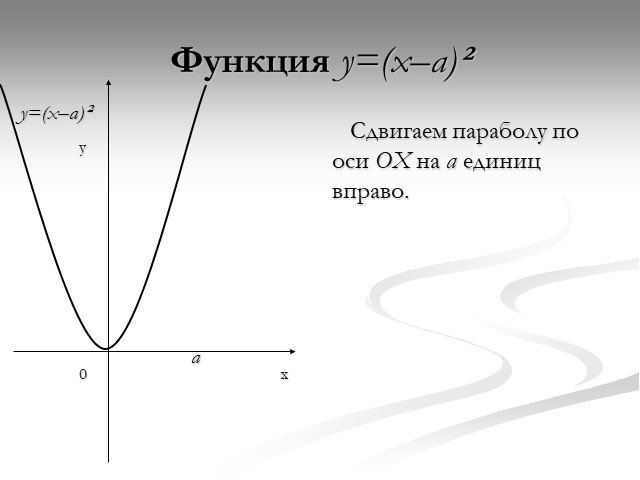
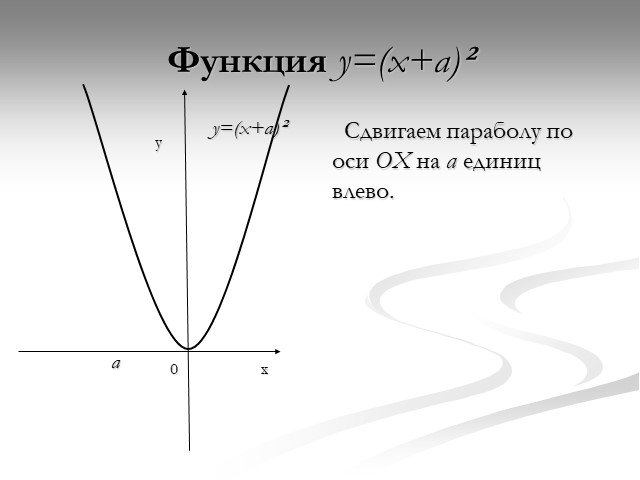
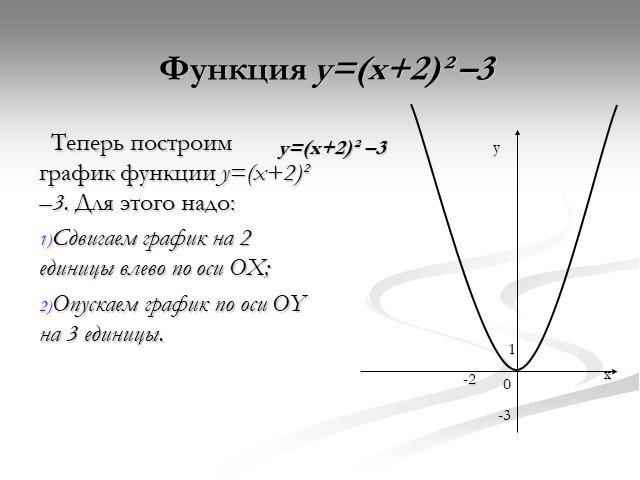
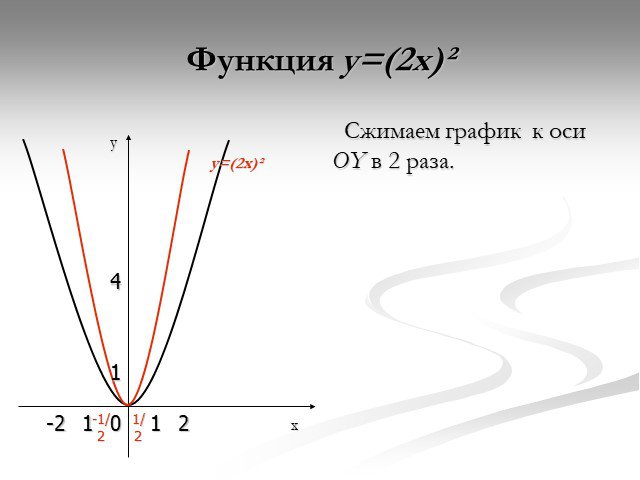
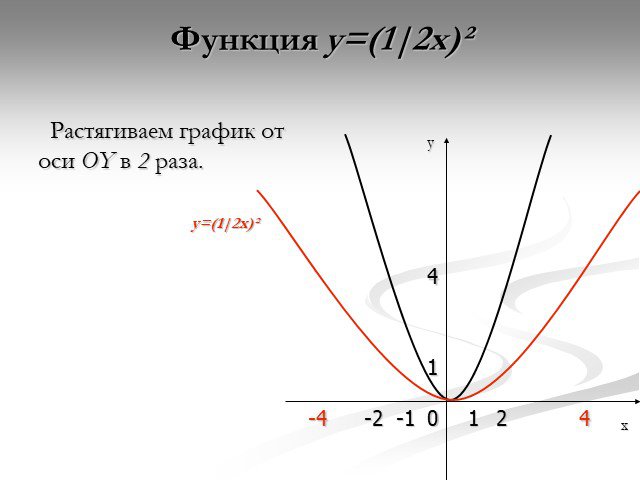
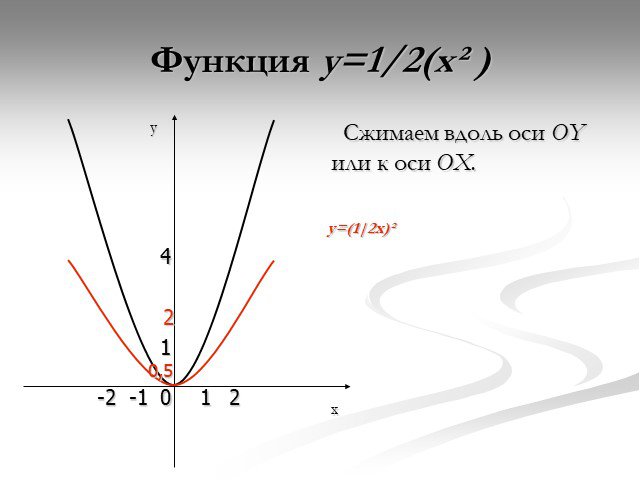
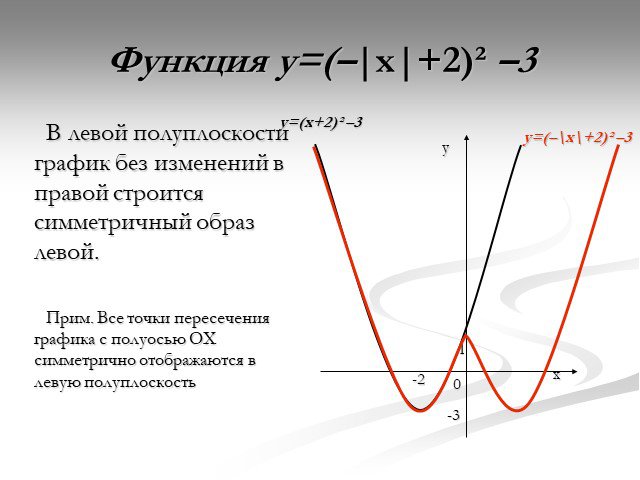
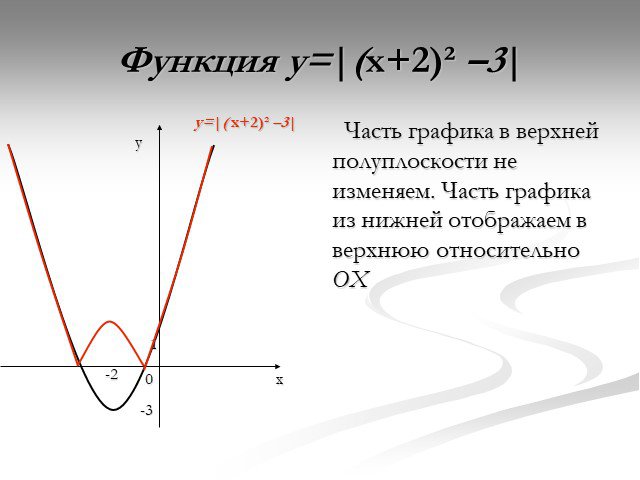
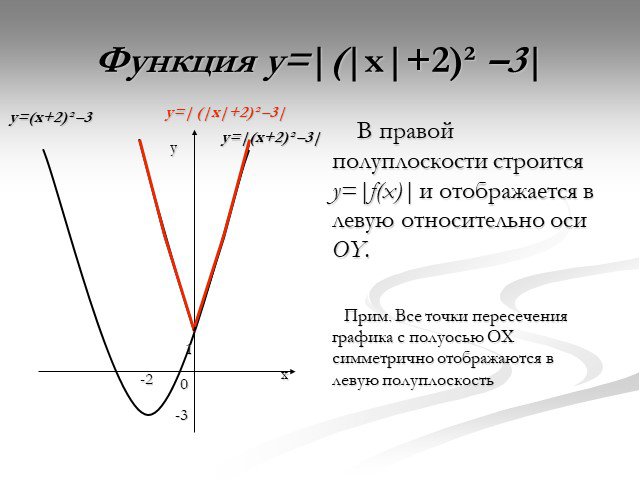
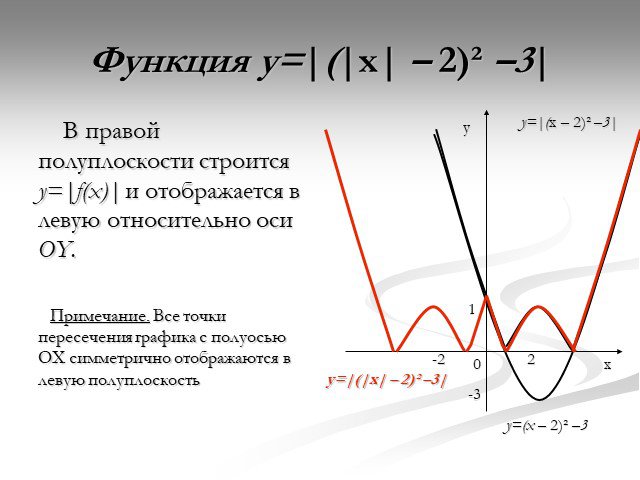
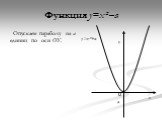
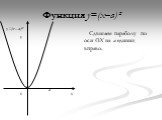
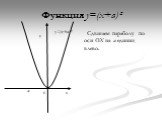
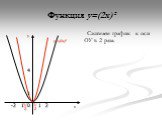
Презентация "Функция y=x2" по математике – проект, доклад
Презентацию на тему "Функция y=x2" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 20 слайд(ов).
Слайды презентации
Список похожих презентаций
Функция у=к/х, её свойства и график
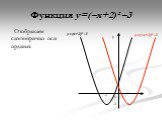
. . - обратная.Графиком является гипербола.
пропорциональность, где k ≠ 0 – заданное число. 1 2 4 6 - - - - - -.
Гипербола в I и III координатных ...
Функция у=кх2, ее свойства и график
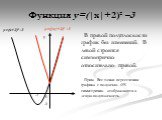
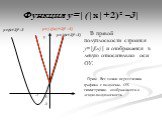
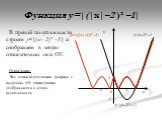
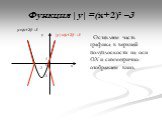
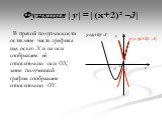
Математику уже затем учить надо, что она ум в порядок приводит. М.В.Ломоносов. Девиз урока:. «Дорогу осилит идущий, а математику- мыслящий». у = 2х2 ...Функция у= модуль х
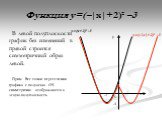
Область определения этой функции - множество R действительных чисел. Пользуясь определением модуля числа х при х > О получим у = х, а при х. Свойства ...Функция у=ах² +вх+с
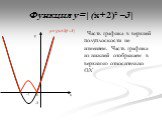
Повторим свойства функции у=ах² при а>0,а. 1)Определите направление ветвей параболы: а) у=3х²; б)у=-1/3х². 2)Выделите полный квадрат из квадратного ...Функция и её график
Задание 1. Решите уравнения:. Задание 2. Сократите дробь:. Задание 3. Найдите площадь фигуры:. Задачи, приводящие к понятию функции. Площадь квадрата ...Функция у = cos х, ее свойства и график
Устно. А) Для ф-ции у=f(х),гдеf(х)=sinх, найти: f(п\6), f(3п\2), f(-п) Б)Упростить: sin(п + х), sin( 3п\2-х), сos(п\2+х), cos(2п-х). В)Как построить ...Функция
Что такое функция? Что называется графиком функции? Какая функция называется линейной? Что является графиком линейной функции? В каком случае графики ...Функция в математике
оглавление. Что такое «функция» Координатная плоскость Что такое «график функции» Декартова координатная плоскость История создания Линейная функция ...Функция
Повторить: свойства функций; методы построения графиков функций; графический способ решения уравнений и систем уравнений. Цели урока. На каком графике ...Функция
Определение функции. Функция – одно из важнейших математических понятий. Функцией называют такую зависимость переменной у от переменной х, при которой ...Функция
Определение функции (функциональной зависимости). Функцией или функциональной зависимостью переменной у от переменной х называется такая зависимость, ...Функция
Актуальность – собрать сведения по теме в связи с подготовкой к экзамену Проблема – в школьном курсе алгебры недостаточно задач с модулем Объект исследования ...Урок по теме Функция
Изучение функций и их свойств. в объёме школьной программы. Методическая тема. Тема урока: «Взаимное расположение графиков линейных функций» Обобщающий ...Функция у=х^3 и её график
Примеры, приводящие к понятию функции. 1. а R зависимая независимая. График функции. Построим график функции по точкам:. х -2 -1,5 -1 -0,5 0 у -8 ...Функция
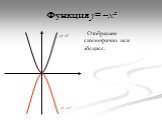
Графиком функции называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям ...I Функция У=АХ², её график и свойства
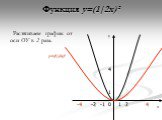
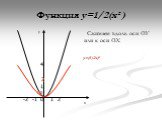
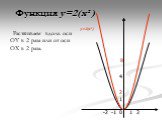
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ...Функция y = ax².
Сегодня на уроке:. введем понятие квадратичной функции научимся строить график функции y=ax2 изучим свойства функции y=ax2. Устная работа 1 задание. ...Функция и её график
Задачи, приводящие к понятию обратной пропорциональности.1.
Пешеход путь S проходит со скоростью v за t часов. Выразите время пешехода через путь ...
Функция y = cos x. Ее свойства и график
Сегодня мы рассмотрим. Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения ...Функция и не функция
Способы задания функции. 1)описать словами 2)формула 3)график 4)таблица. Формула. Формула-вид математического выражения, записанное условными математическими ...Конспекты
Функция у=х^n ее свойства и график
Открытый урок в 9классе по теме:”Функция у=х^. n. ее свойства и график. “. Цели урока: систематизация ЗУН по теме,. активизация мыслительной деятельности,. ...Функция у=к/х
Открытый обобщающий урок по алгебре в 8 классе по теме «Функция у=к/х». «Знатоки гиперболической функции». Цели урока:. Образовательная:. обобщить ...Функция у=к/х и её график
Открытый урок по алгебре в 8 А классе. . учителя Никитиной Ирины Александровны. Тема. :. Функция у=к/х и её график. (2-й урок в теме). Цель. ...Функция у=ах^2 , её свойства и график
. Конспект урока по теме:. . «Функция у=ах^2 , её свойства и график». . 8 класс. Выполнила: учитель математики. . ГБОУ школы ...Функция у=ах2 и ее свойства
. План-конспект урока. . по алгебре 8 класс. Учителя математики. Гринёвой Татьяны Васильевны. Ростовской области. . МБОУ Тацинской ...Функция y = k/x и её график
ФИО автора материала. Белых Олеся Валерьевна. . . Место работы: МБОУ «Верхнедеревенская СОШ» Льговского района Курской области. . Должность: ...Функция у=
ПЛАН-КОНСПЕКТ УРОКА. Тема урока: «Функция у=. ». . ФИО (полностью):. . Скурлатова Ольга Викторовна. . . . Место работы:. ...Функция и ее график
Тема: «Функция. и ее график». Цели:. . Сформулировать определение обратной пропорциональности, научить находить значение функции и аргумента ...Функция у = √Х и её график.
Открытый урок. в. VIII. классе. ТЕМА:. «Функция у = √Х и её. график.». г. Минеральные Воды 2011 -2012 уч.год. . учитель:Здвижко Екатерина ...Функция y=sin x ее свойства и график
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 47 с углубленным изучением отдельных предметов. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Содержит:20 слайд(ов)
Поделись с друзьями:
Скачать презентацию