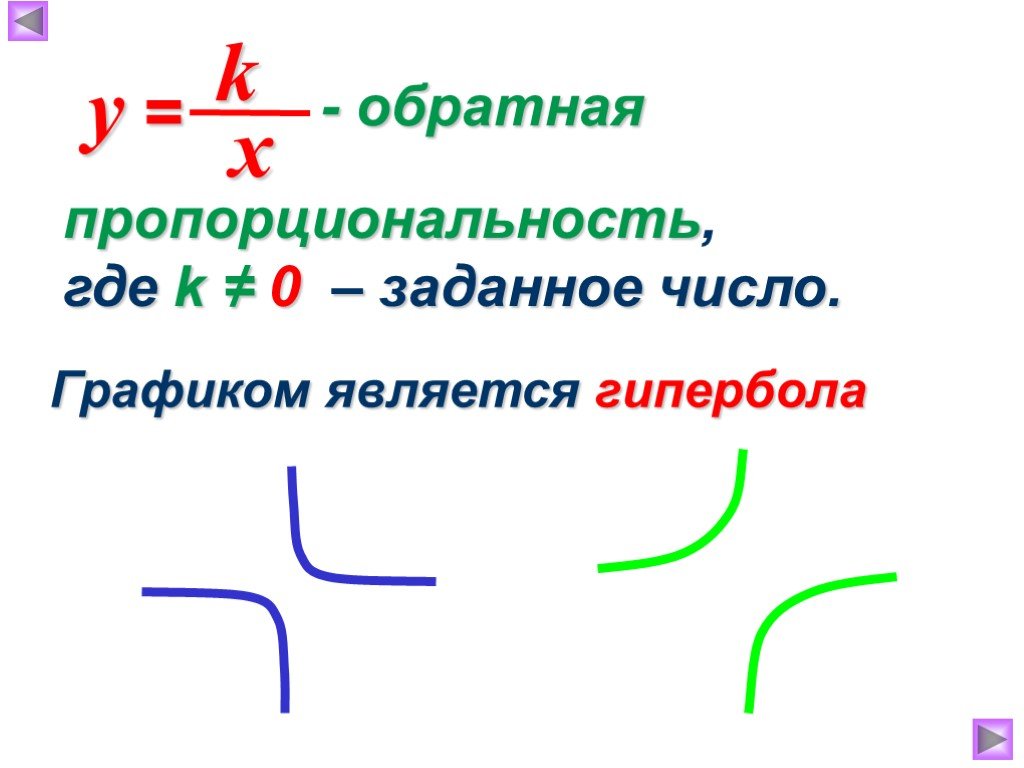
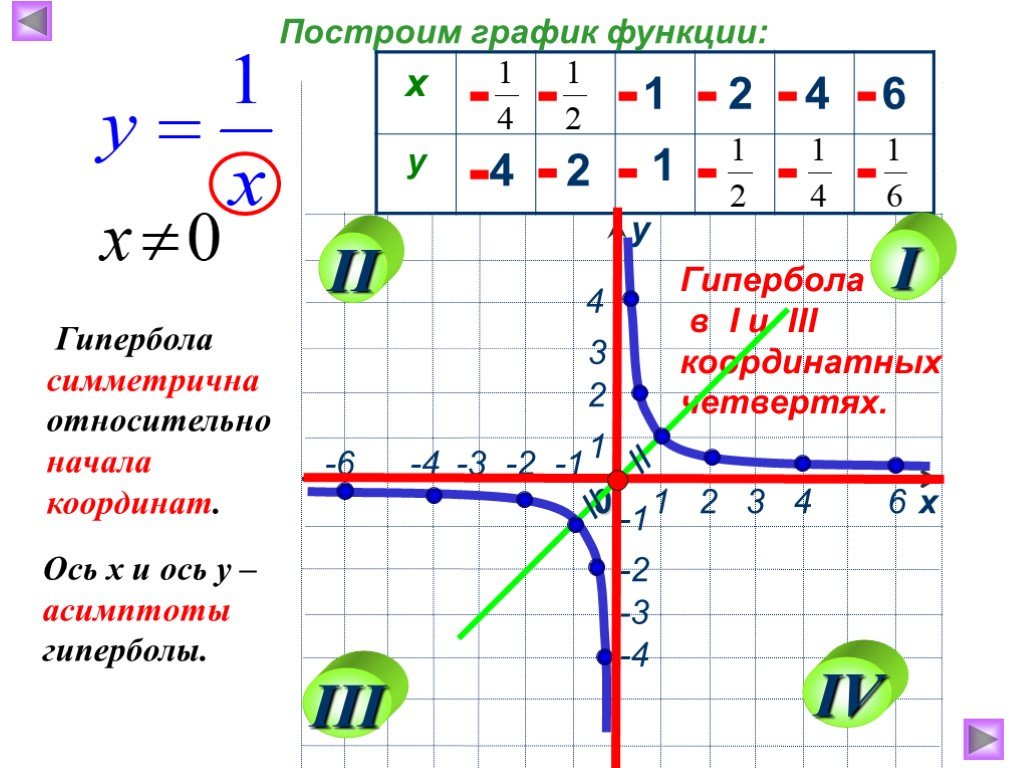
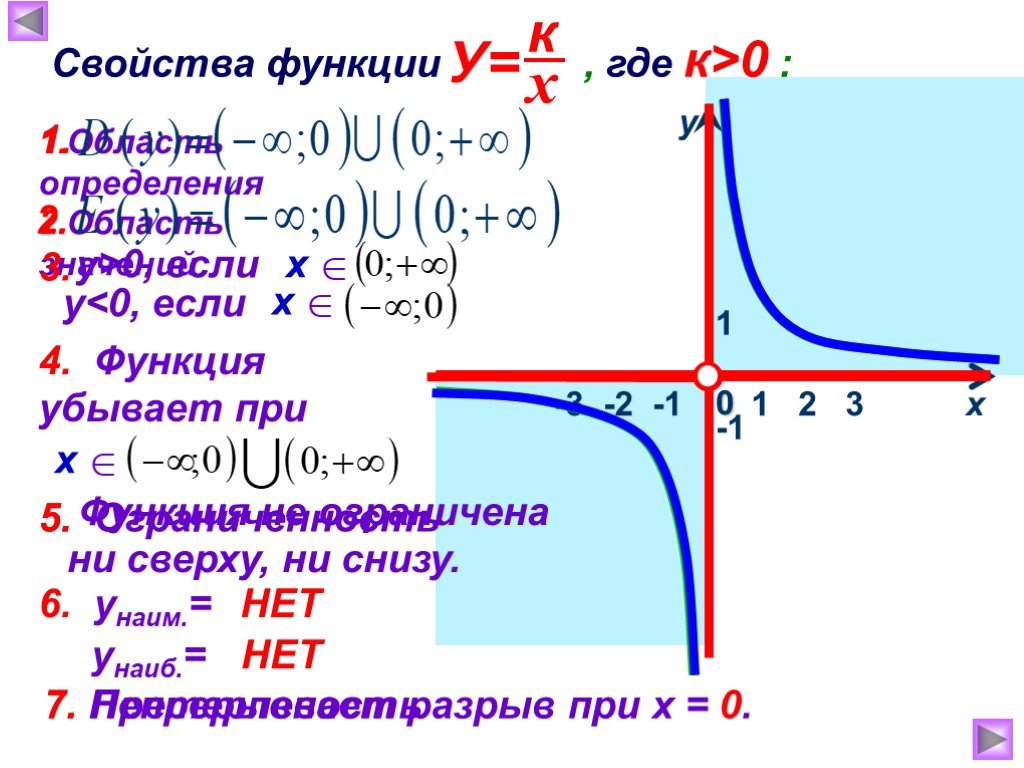
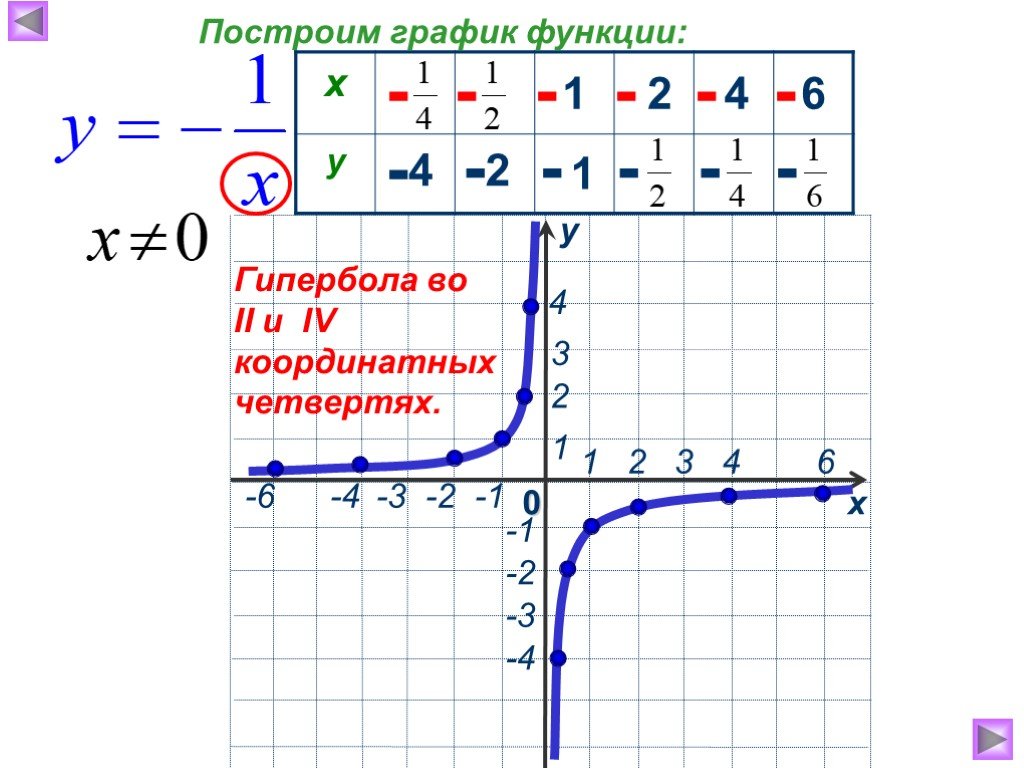
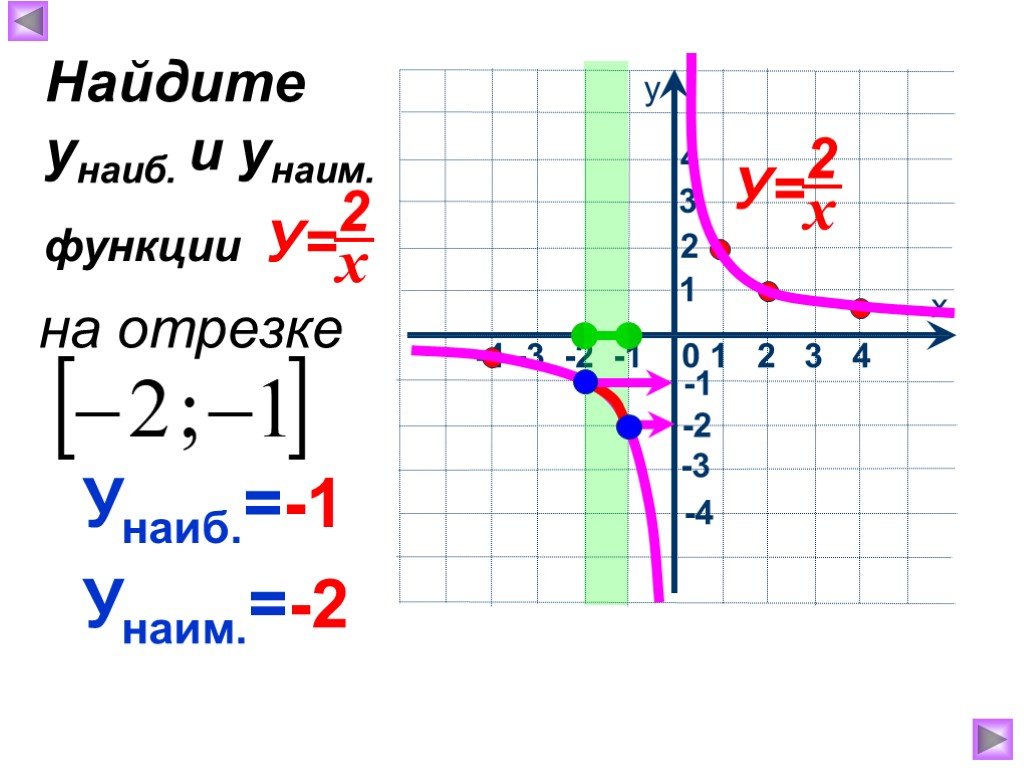
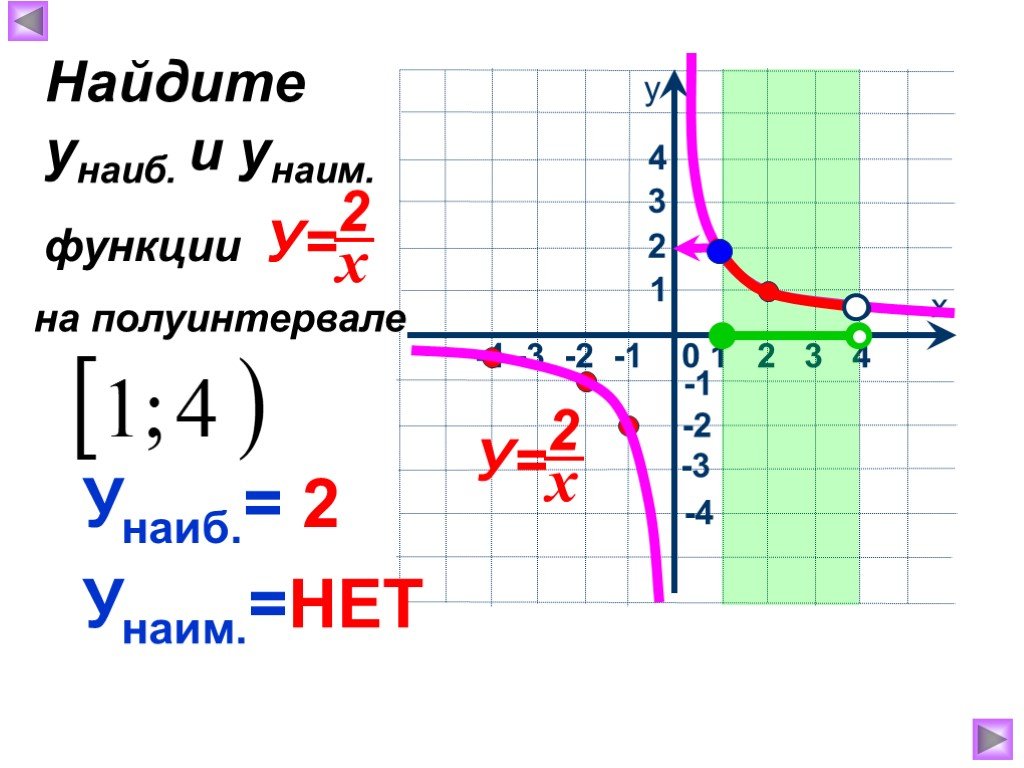
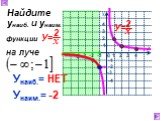
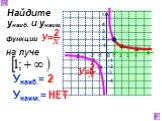
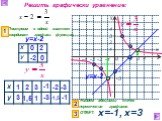
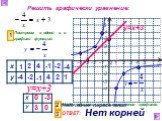
Презентация "Функция у=к/х, её свойства и график" по математике – проект, доклад
Презентацию на тему "Функция у=к/х, её свойства и график" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
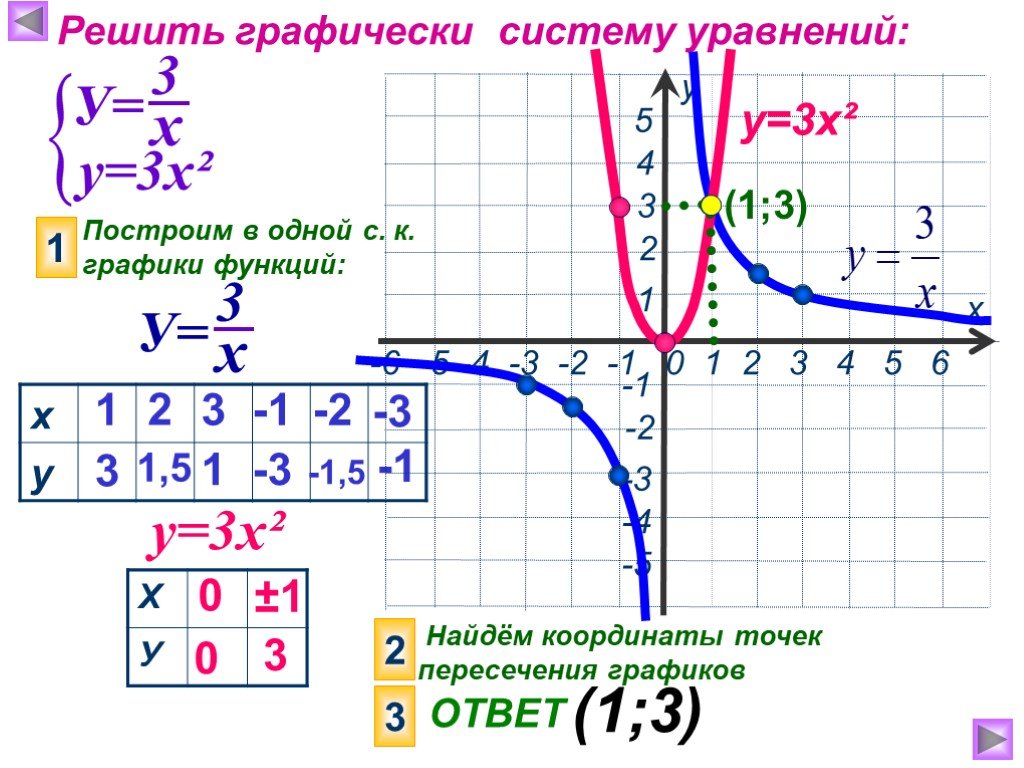
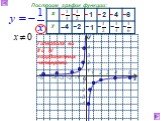
I Функция У=АХ², её график и свойства
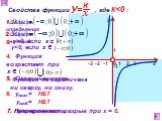
А=1 У=Х ². А=2 У=2Х ². У=Х² У=2Х². Растяжение от оси Х в два раза. А=0.5 У=Х² У=0.5Х². Сжатие по оси Х в два раза. Вообще график функции У=АХ² можно ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Cфера и шар
Что такое сфера и шар? геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние ...«Умножение и деление»
Цели урока. Обобщение и систематизация знаний, умений и навыков по теме: «Умножение и деление натуральных чисел»; контроль уровня усвоения темы. Развитие ...«Табличное умножение и деление» Устный счёт
Решите задачу: Во раз б 9 шт. 3 шт.. 9:3=3 (раза)- во столько раз апельсинов больше, чем яблок. 7∙5=35 (яб.). У резной избушки На лесной опушке Бельчата ...«Сложение и вычитание десятичных дробей»
Чтобы сложить (вычесть) десятичные дроби, нужно: 1) уравнять в этих дробях количество знаков после запятой; 2) записать их друг под другом так, чтобы ..."Умножение и деление чисел"
Тема урока:. Умножение и Деление чисел. В наше время, чтобы строить И машиной управлять, Помни друг, что надо прочно Математику познать! Математический ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ..."Сложение положительных и отрицательных чисел"
Старостенко Алла Николаевна, учитель математики Предмет: математика, урок-игра, закрепление изученного материала Тема: «Сложение положительных и отрицательных ..."Сложение и вычитание рациональных чисел"
I. II. III. IV. Тема: "Сложение и вычитание положительных и отрицательных чисел". Станции: Историческая Биологическая Географическая Математическая. ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
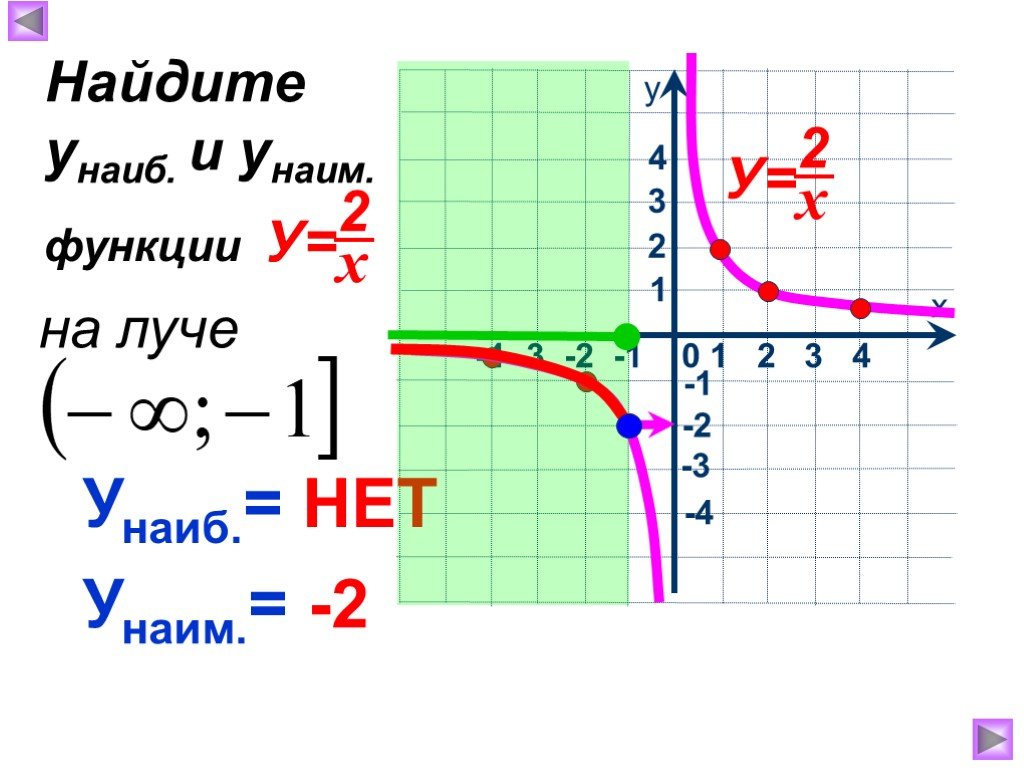
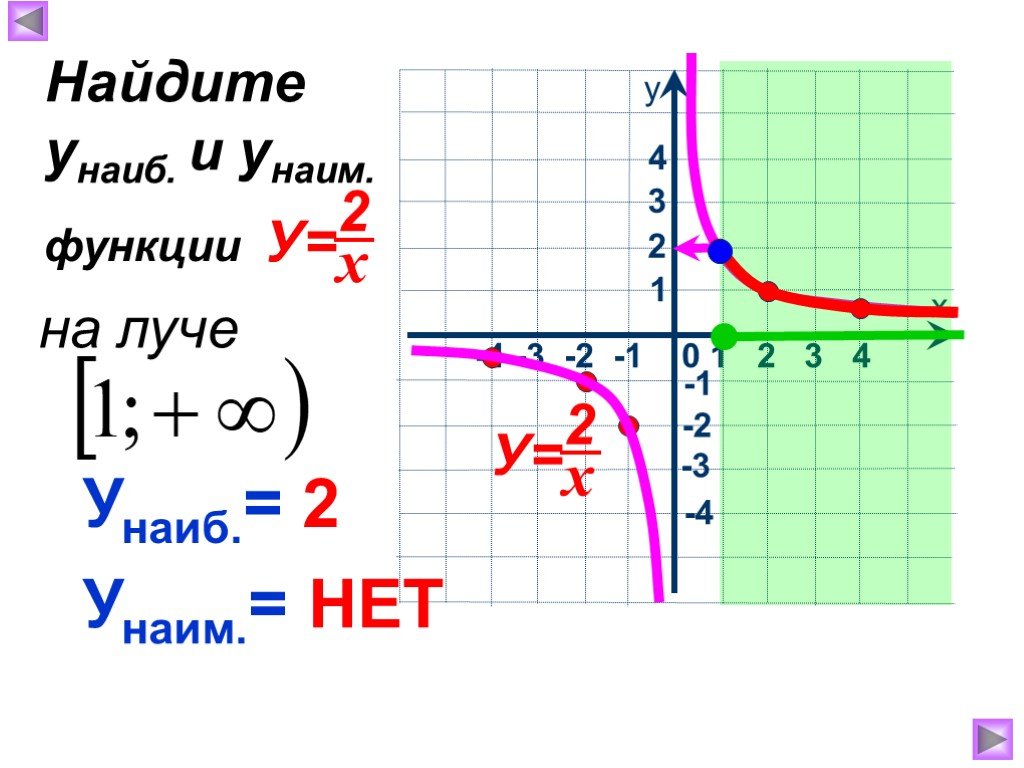
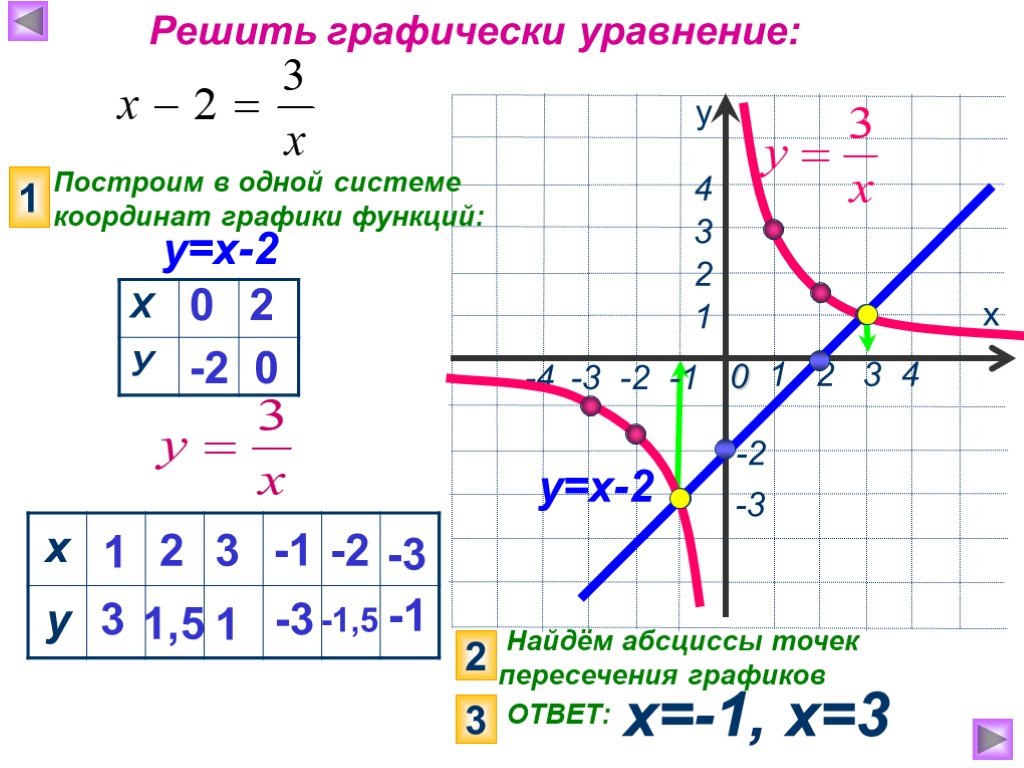
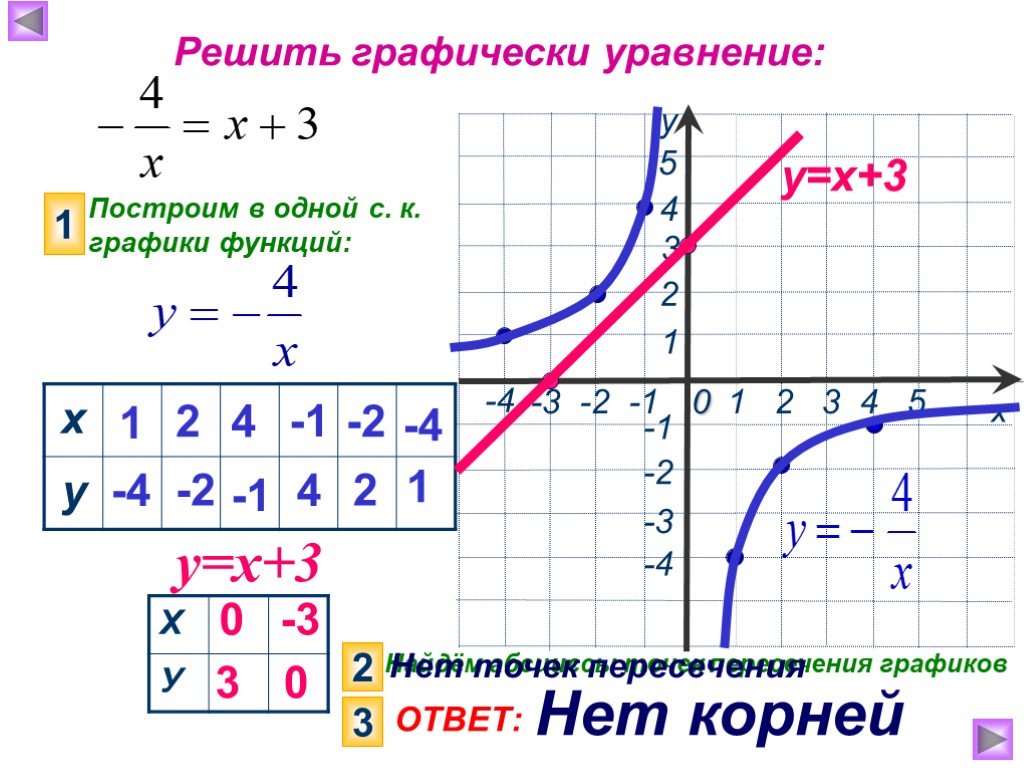
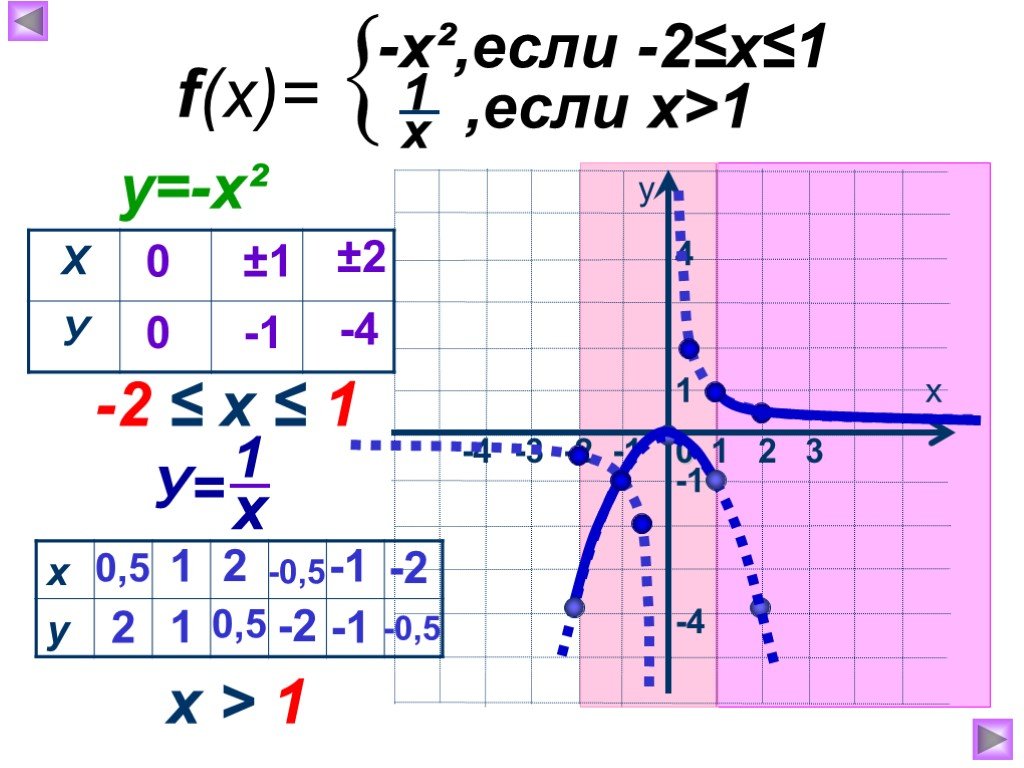
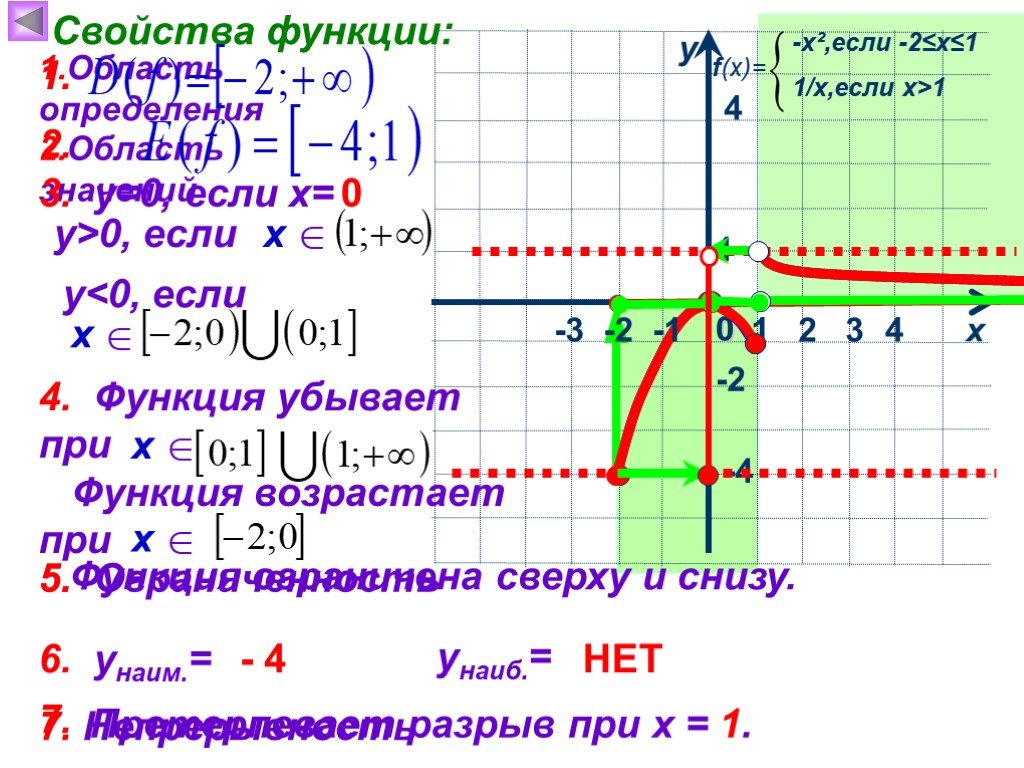
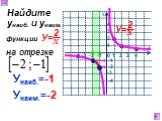
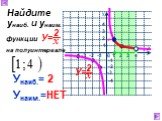
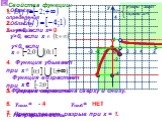
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ..."Комбинаторика и вероятность"
Диктант ******- это раздел математики, посвященный задачам выбора и расположения предметов из различных множеств. Произведение натуральных чисел от ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ...«Сложение положительных и отрицательных чисел».
. Кемеровская область. Если в картину Сибири всмотреться, На ней обозначены контуры сердца. И бьется оно. И отчизна внимает Рабочему ритму Кузнецкого ..."Число и цифра 9"
Число и цифра 9. Тема урока:. Цель урока:. познакомить с числом 9, обучить написанию цифры 9. Задачи урока:. вспомнить времена года, дни недели, месяцы; ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ...Конспекты
Арифметический квадратный корень и его свойства
Урок - повторение по теме: «Арифметический квадратный корень и его свойства». . . Учитель Переверзева М.В. МБОУСОШ «11. . Цель: подвести итоги ...Арифметический квадратный корень и его свойства
Конспект урока математики в 10 классе. Жирнова С.В. учитель математики. Тема урока:. «Арифметический квадратный корень и его свойства». Тип урока. ...Арифметический корень натуральной степени и его свойства
Урок алгебры в 9 классе. . Тема урока. : «Арифметический корень натуральной степени и его свойства». . Из опыта работы учителя математики. ...Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов
Алгоритм и его свойства. Запись алгоритмов. Виды алгоритмов. . КАЗАХСТАН. ЮЖНО-КАЗАХСТАНСКАЯ ОБЛАСТЬ. Г.ШЫМКЕНТ, ОСНОВНАЯ СРЕДНЯЯ ШКОЛА №97. ...Арифметический квадратный корень и его свойства
Тема: «Арифметический квадратный корень и его свойства». Урок-игра «Аукцион математических знаний». Цели урока. :. . Образовательные:. - ...В гостях у Геометрии. Внутри и снаружи
. Муниципальное бюджетное образовательное учреждение. «Черемшанская средняя общеобразовательная школа № 1». Черемшанского муниципального района ...Буквенная запись свойств сложения и вычитания
Муниципальное автономное общеобразовательное учреждение. Чурилковская средняя общеобразовательная школа. Домодедовского района Московской области. ...Бинарный урок математики и кубановедения. Проценты
Бинарный урок математики и кубановедения. Проценты. Цель урока:. воспитательные:. - активизация познавательной и творческой деятельности учащихся;. ...Белоснежка и семь гномов
Муниципальное автономное дошкольное общеобразовательное учреждение. «Детский сад комбинированного вида» №221. Кемеровской области. Конспект ...Верные и неверные равенства и неравенства
Муниципальное бюджетное образовательное учреждение. средняя общеобразовательная школа №1. . города Ярцева Смоленской области. . Конспект ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:30 мая 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию