Слайд 1Квадратные уравнения
Слайд 2Содержание.
Введение. Основная часть. Заключение. Список используемой литературы.
Слайд 3Введение.
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами. Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Умение быстро, рационально и правильно решать квадратные уравнения облегчает прохождение многих тем курса математики:в разложении квадратного трехчлена, в исследовании квадратичной функции, в решении уравнений высших степеней, в решении текстовых задач и задач по геометрии. Содержание
Слайд 4Основная часть.
Из истории. Определение. Виды квадратных уравнений. Практикум. содержание
Слайд 5Из истории.
Квадратные уравнения в Древнем Вавилоне. Квадратные уравнения в Индии. Квадратные уравнения в Европе 13-17в.в. Основная часть

Слайд 6Кв. уравнения в Древнем Вавилоне из истории
Необходимость решать уравнения не только первой, но и второй степени ёщё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей веры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводя только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Слайд 7Кв. уравнения в Индии из истории
Задачи на квадратные уравнения встречаются уже в 499 г. В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: "Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи. Задача знаменитого индийского математика Бхаскары: Обезьянок резвых стая Всласть поевши, развлекаясь. Их в квадрате часть восьмая На поляне забавлялась. А 12 по лианам..... Стали прыгать, повисая. Сколько было обезьянок, Ты скажи мне, в этой стае?

Слайд 8Квадратные уравнения в Европе 13-17 в.в. из истории
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х2+вх+с=0, было сформулировано в Европе лишь в 1544 г. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Слайд 9Определение основная часть
Уравнение вида ax2+bx+c=0, где a, b, c - действительные числа, причем a не равно 0, называют квадратным уравнением. Если a = 1 , то квадратное уравнение называют приведенным; если a ¹ 1, то неприведенным . Числа a, b, c носят следующие названия:a -первый коэффициент, b - второй коэффициент, c - свободный член. Корни уравнения ax2+bx+c=0 находят по формуле Выражение D = b2- 4ac называют дискриминантом квадратного уравнения. Если D 0, то уравнение имеет два действительных корня. В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня. Используя обозначение D = b2- 4ac, можно переписать формулу в виде Если b = 2k, то формула принимает вид: Итак, где k = b / 2. Последняя формула особенно удобна в тех случаях, когда b / 2 - целое число, т.е. коэффициент, b - четное число.

Слайд 10Виды квадратных уравнений.
Неполные кв. уравнения. Полное кв. уравнение. Теорема Виета. Теорема, обратная теореме Виета. Кв. уравнения с комплексными переменными. Решение кв. уравнений с помощью графиков. Разложение кв. трехчлена на множители. Биквадратные уравнения Уравнения с параметрами. Основная часть
Слайд 11Неполные кв. уравнения виды кв. уравнений
Если в квадратном уравнении ax2+bx+c=0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным. Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения - проще решить уравнение методом разложения его левой части на множители. Способы решения неполных квадратных уравнений: 1) c = 0 , то уравнение примет вид ax2+bx=0. x( ax + b ) = 0 , x = 0 или ax + b = 0 , x = -b : a . 2) b = 0, то уравнение примет вид ax2 + c = 0 , x2 = -c : a , x1 = или x2 = - 3) b = 0 и c = 0 , то уравнение примет вид ax2 = 0, x =0.
Слайд 12Полное квадратное уравнение виды кв. уравнений
Если в квадратном уравнении второй коэффициент и свободный член не равны нулю, то такое уравнение называют полным квадратным уравнением.
Слайд 13Теорема Виета виды кв. уравнений
Теорема. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Доказательство. Рассмотрим приведённое квадратное уравнение. Обозначим второй коэффициент буквой p, а свободный член - буквой q: Дискриминант этого уравнения D равен Пусть D>0 .Тогда это уравнение имеет два корня: и Найдём сумму и произведение корней:

Слайд 14Теорема, обратная теореме Виета. виды кв. уравнений
Теорема. Если числа m и n таковы, что их сумма равна –p, а произведение равно q, то эти числа являются корнями уравнения Доказательство. По условию m+n=-p,а mn=q. Значит, уравнение можно записать в виде Подставив вместо x число m, получим: Значит, число m является корнем уравнения. Аналогично можно показать, что число n так же является корнем уравнения: По праву в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни и дробь уж готова: В числителе С, в знаменателе А, А сумма корней тоже дроби равна Хоть с минусом дробь эта, что за беда- В числителе b, в знаменателе a.

Слайд 15Кв. уравнения с комплексными переменными виды кв. уравнений
Сначала рассмотрим простейшее квадратное уравнение где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение: 1)Имеет один корень z=0, если а=0; 2)Имеет два действительных корня , если а>0. 3)Не имеет действительных корней, если a
Слайд 16Решение кв. уравнений с помощью графиков. виды кв. уравнений
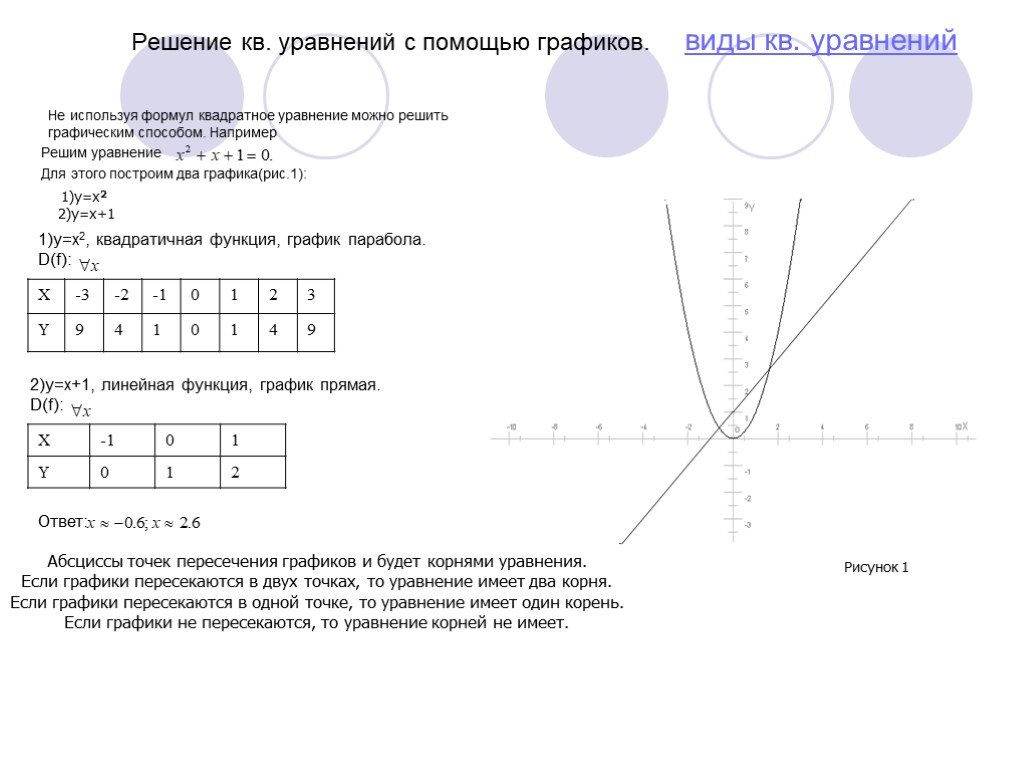
Не используя формул квадратное уравнение можно решить графическим способом. Например Решим уравнение Для этого построим два графика(рис.1):
1)y=x2 2)y=x+1
1)y=x2, квадратичная функция, график парабола. D(f):
2)y=x+1, линейная функция, график прямая. D(f):
Рисунок 1 Ответ:
Абсциссы точек пересечения графиков и будет корнями уравнения. Если графики пересекаются в двух точках, то уравнение имеет два корня. Если графики пересекаются в одной точке, то уравнение имеет один корень. Если графики не пересекаются, то уравнение корней не имеет.
Слайд 17Разложение кв. трехчлена на множители виды кв. уравнений
Многочлен вида ax2+bx+c, где a,b,c - некоторые числа, x переменная, называется квадратным трёхчленом. Пример 3x2+7x+9 Квадратный трехчлен разлагается на множители , где и корни трехчлена. Дано: - квадратный трехчлен; и -корни его Доказать: Доказательство: по теореме Виета следует,

Слайд 18Биквадратные уравнения виды кв. уравнений
Решение квадратных уравнений широко применяется в других разделах математики: в разложении квадратного трехчлена, в исследовании квадратичной функции, в решении уравнений высших степеней, в решении текстовых задач и задач по геометрии. Некоторые уравнения высших степеней можно решить, сведя их к квадратному. 1) Иногда левую часть уравнения легко разложить на множители, из которых каждый - многочлен не выше 2-ой степени. Тогда приравнивая каждый многочлен к нулю, решаем полученные уравнения. ПРИМЕР: 2) Если уравнение имеет вид ax2n+bxn+c= 0, его можно свести к квадратному, введя новую переменную t = x. ПРИМЕР: 3) В геометрии: Гипотенуза прямоугольного треугольника равна 10. Найти катеты, если один из них на 2 см. больше другого. РЕШЕНИЕ: по теореме Пифагора a2+ b2= c2 Пусть х см.-1 катет, тогда (х+2) см.-2 катет. Составим уравнение: x2+ (x+2)2= 102 Пифагор

Слайд 19Уравнения с параметрами(1) виды кв. уравнений
Линейные и квадратные уравнения. Линейное уравнение, записанное в общем виде, можно рассматривать как уравнение с параметрами : ах = b, где х –неизвестное, а, b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном. При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него. Особым значением параметра а является значение а = 0. 1. Если а ≠ 0 , то при любой паре параметров а и b оно имеет единственное решение х = . 2. Если а = 0, то уравнение принимает вид: 0 х = b. В этом случае значение b = 0 является особым значением параметра b. При b ≠ 0 уравнение решений не имеет. При b = 0 уравнение примет вид : 0 х = 0. Решением данного уравнения является любое действительное число.

Слайд 20Уравнения с параметрами(2) виды кв. уравнений
Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами. Такие буквы называются параметрами. Предполагается, что эти параметры могут принимать любые числовые значения, т.е. одно уравнения с параметрами задаёт множество уравнений (для всех возможных значений параметров). Например, линейное уравнение ax + b = c с неизвестным x можно рассматривать как уравнение с параметрами a, b, и c. Его решением при a ¹ 0 является x = (c - b) / a. Если a = 0, то получается “уравнение” b = c, и если действительно b = c, то корнями данного уравнения являются все действительные числа. Если же b ¹ c, при этом a = 0, то данное уравнение корней не имеет. Так, с параметрами учащиеся встречаются при введении некоторых понятий. Не приводя подробных определений, рассмотрим случай в качестве примеров следующие объекты: · функция прямая пропорциональность: y = kx (x и y — переменные; k — параметр,k ¹ 0); · линейная функция: y = kx + b (x и у — переменные, k и b —параметры); · линейное уравнение: ax + b = 0 (x — переменная; a и b —параметры); · уравнение первой степени: ax + b = 0 (x — переменная; a и b — параметры, a ¹ 0); · квадратное уравнение: ax2 + bx + c = 0 (x — переменная; a, b и c — параметры, a ¹ 0). Решить уравнение с параметрами означает следующее: 1) исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров. 2) Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения. Ответ к задаче “решить уравнение с параметрами” должен выглядеть следующим образом: уравнение при таких-то значениях параметров имеет корни …, при таких-то значениях параметров — корни …, при остальных значениях параметров уравнение корней не имеет.

Слайд 21Практикум.
Неполные кв. уравнения Метод выделения полного квадрата. Решение кв. уравнений по формуле b2-4ac Приведённые кв. уравнения. Теорема Виета Решение кв. уравнений по теореме обратной т. Виета Решение задач с помощью кв. уравнений. Решение кв. уравнений по формуле k2-ac. Решение уравнений с параметрами Проверь себя! Основная часть
Слайд 22Стр.1 Практикум назад
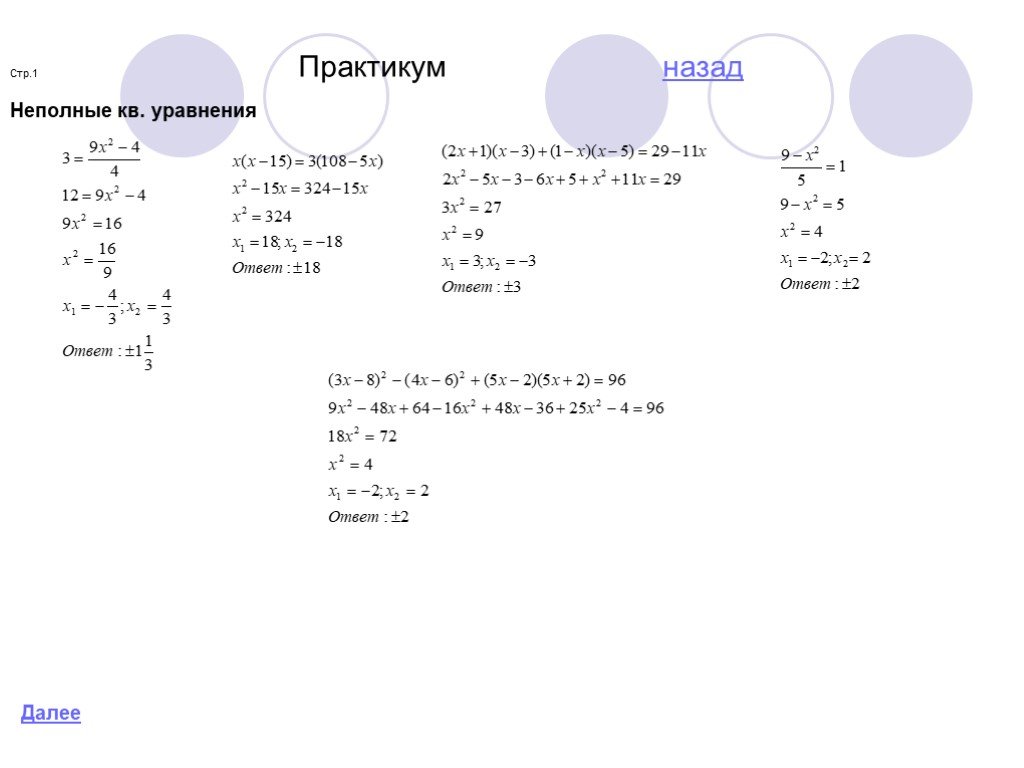
Неполные кв. уравнения Далее
Слайд 23Стр.2 Практикум назад
Метод выделения полного квадрата. Далее
Слайд 24Стр.3 Практикум назад
Решение кв. уравнений по формуле b2-4ac Далее
Слайд 25Стр.4 Практикум назад
Приведённые кв. уравнения. Теорема Виета Записать приведённое кв. уравнение, имеющее корни : 1) 2) 3) 4) Решение Воспользуемся т.Виета. Далее
Слайд 26Стр.5 Практикум назад
Решение кв. уравнений по теореме обратной т. Виета Далее
1)Составьте уравнение, если
q= p=
2)Составьте уравнение, если
3)Составьте уравнение, если
4)Составьте уравнение, если
5)Составьте уравнение, если
Слайд 27Стр.6 Практикум назад
Расстояние между начальным и конечным пунктами следования поезда 600 км. На расстоянии 150км. от начального пункта поезд задержался на 1,5 часа. Для того, что бы поезд пришёл по расписанию, ему пришлось увеличить скорость на 15 км\ч. Найдите время нахождения поезда в пути. Решение задач с помощью кв. уравнений. Процессы Скорость км/ч Время ч. Расстояние км. Поезд до задержки x 150 Поезд после задержки x+15 450 По расписанию x 600 _____________________________________________________________________ Зная, что поезд был задержан на 1,5 часа, сост.ур ОДЗ Далее

Слайд 28Стр.7 Практикум назад
Катер прошёл вверх по реке 35 км. затем по протоке 18 км. против течения. На всё путешествие он затратил 8 часов. Найдите скорость течения реки, зная, что скорость катера в стоячей воде 10 км\ч, а скорость течения в протоке на 1 км\ч больше чем в реке. Решение задач с помощью кв. уравнений. Процессы Скорость км/ч Время ч. Расстояние км. Вверх по реке 10-x 35 Вверх по протоку 10-(x+1) 18 V течения x V притока x+1 _____________________________________________________________ Зная, что скорость в стоячей воде равна 10 км/ч, сост.ур ОДЗ Далее
Слайд 29Стр.8 Практикум назад
За 2 года население выросло с 20000 человек до 22050 человек. Найти ежегодный % прироста населения. Решение задач с помощью кв. уравнений. Было Изменилось Стало Первый год 20000 200x 20000+200x Второй год 20000+200x 200x+2x 20000+400x+2x _____________________________________________________________________ Зная, что за 2 года население около 22050, составим уравнение Ответ:5% Далее
Слайд 30Стр.9 Практикум назад
Решение кв. уравнений по формуле k2-ac.
т.к. D1 Далее

Слайд 31Стр. 10 Практикум назад
Решение уравнений с параметрами П р и м е р . Решим уравнение 2а(а — 2) х = а — 2. Р е ш е н и е. Здесь контрольными будут те значения параметра, при которых коэффициент при х обращается в 0. Такими значениями являются а=0 и а=2. При этих значениях а невозможно деление обеих частей уравнения на коэффициент при х. В то же время при значениях параметра а≠0, а≠2 это деление возможно. Таким образом, целесообразно множество всех действительных значений параметра разбить на подмножества A1={0}, А2={2} и Аз = {а≠0, а≠2} и решить уравнение (2) на каждом из этих подмножеств, т. е. решить уравнение как семейство уравнений, получающихся из него при следующих значениях параметра: 1) а=0 ; 2) а=2 ; 3) а≠0, а≠2 Рассмотрим эти случаи. 1) При а=0 уравнение принимает вид 0 х = — 2. Это уравнение не имеет корней. 2) При а=2 уравнение принимает вид 0 х=0. Корнем этого уравнения является любое действительное число. 3) При а≠0, а≠2 из уравнения получаем, х = откуда х = . 0 т в е т: 1) если а=0, то корней нет; 2) если а=2, то х — любое действительное число; 3) если а≠0, а≠2 , то х = Далее

Слайд 32Стр. 11 Практикум назад
Пример 1. Решите уравнение Решение Найдем недопустимые значения a: Ответ. Если если a = – 19, то корней нет.
Пример 2. Решите уравнение Решение Найдем недопустимые значения параметра a: 10 – a = 5, a = 5; 10 – a = a, a = 5. Ответ. Если a = 5, то уравнение теряет смысл; если a¹5, то x=10–a.

Слайд 33Тест назад
ТЕСТ (англ. test проба, испытание, исследование), 1) В психологии и педагогике стандартизированного задания, по результатам выполнения которых судят о психофизиологических и личностных характеристиках, а также знаниях, умении и навыках испытуемого. 2) В физиологии и медицине пробные воздействия на организм с целью изучения различных физиологических процессов в нем, а также для определения функционального состояния отдельных органов, тканей и организма в целом. 3) В вычислительной технике контрольная задача для проверки правильности работы ЭВМ. 4) В распознавании образов множество функционально взаимозависимых признаков, характеризующих образ (класс). Тесты – это реальная возможность проверить свои накопленные знания. Попробуй, проверь себя! Вперёд! Удачи!
Перейти к тесту
Слайд 34Неполные квадратные уравнения назад
Задание №1. Самостоятельно решите уравнения : 1) 3x2 + 4x = 0, 2) 2x2- 2 =0, 3) 5x2 =0, 4) 3х2 – 2х = 0, 5) 2х2 – 7 = 0, 6) -x2 + 9 = 0.
Слайд 35Решение квадратных уравнений по формуле b2 - 4ac назад
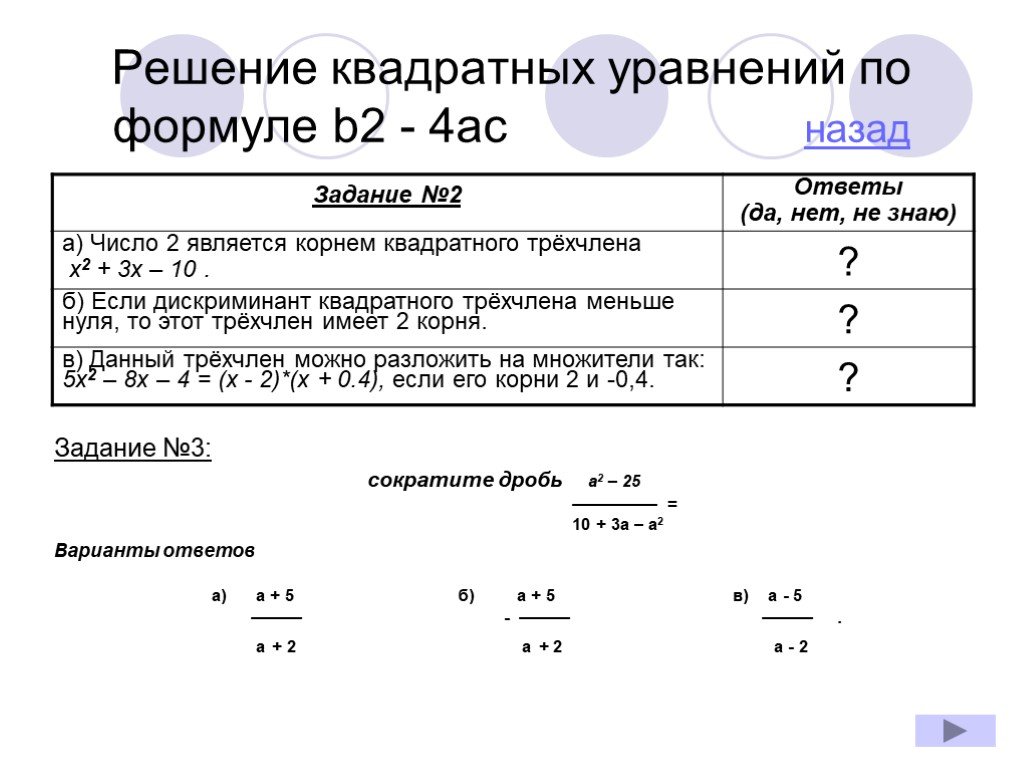
Задание №3: сократите дробь a2 – 25 ————— = 10 + 3a – a2 Варианты ответов а) a + 5 б) a + 5 в) a - 5 ——— - ——— ——— . a + 2 a + 2 a - 2
Слайд 36Решение задач с помощью квадратных уравнений назад
Задание №4 Решите задачу. а) Два пешехода одновременно выходят навстречу друг другу из пунктов A и B и встречаются через полчаса. Продолжая движение, первый прибывает в B на 1 мин раньше, чем второй в пункт A. За какое время преодолел расстояние каждый пешеход? б) Сплав золота с серебром, содержащий 80 г золота, сплавлен со 100 г чистого золота. В результате содержание золота в сплаве повысилось по сравнению с первоначальным на 20%. Сколько серебра в сплаве?
Слайд 37Решение уравнений с параметрами назад
Задание №5 Решите уравнения: 1. x – a = 0; 2. x + a = 1; 3. 2x = a 4. x + y= 2; 5. ах = 3
Слайд 38Квадратичная функция и её график.
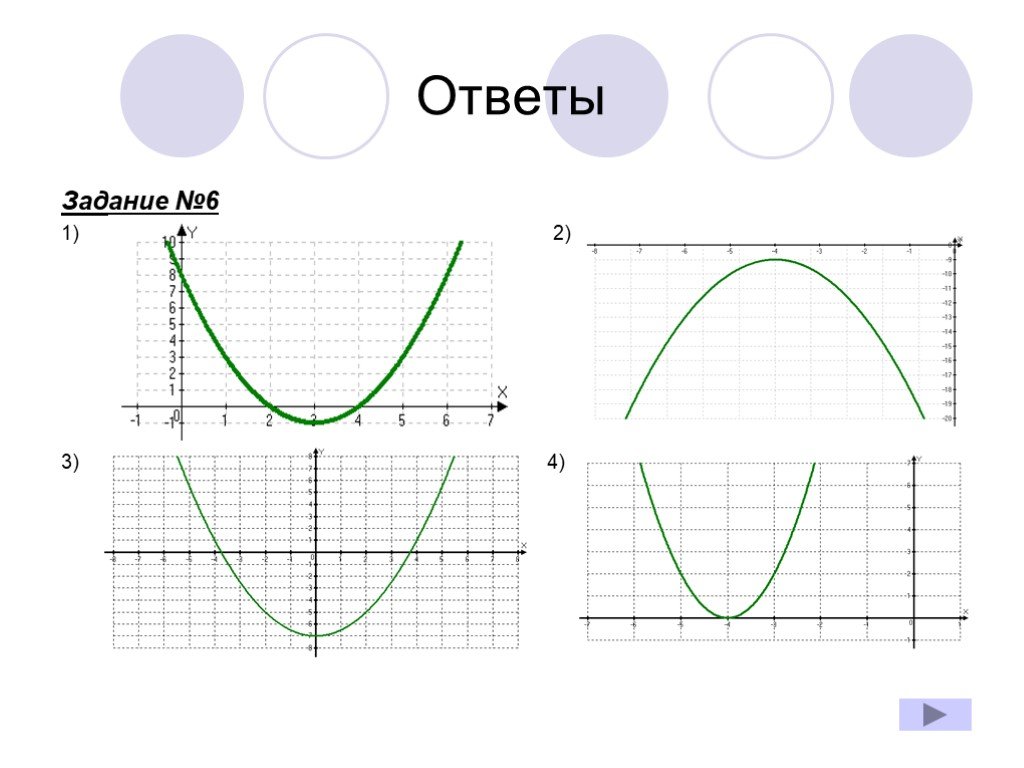
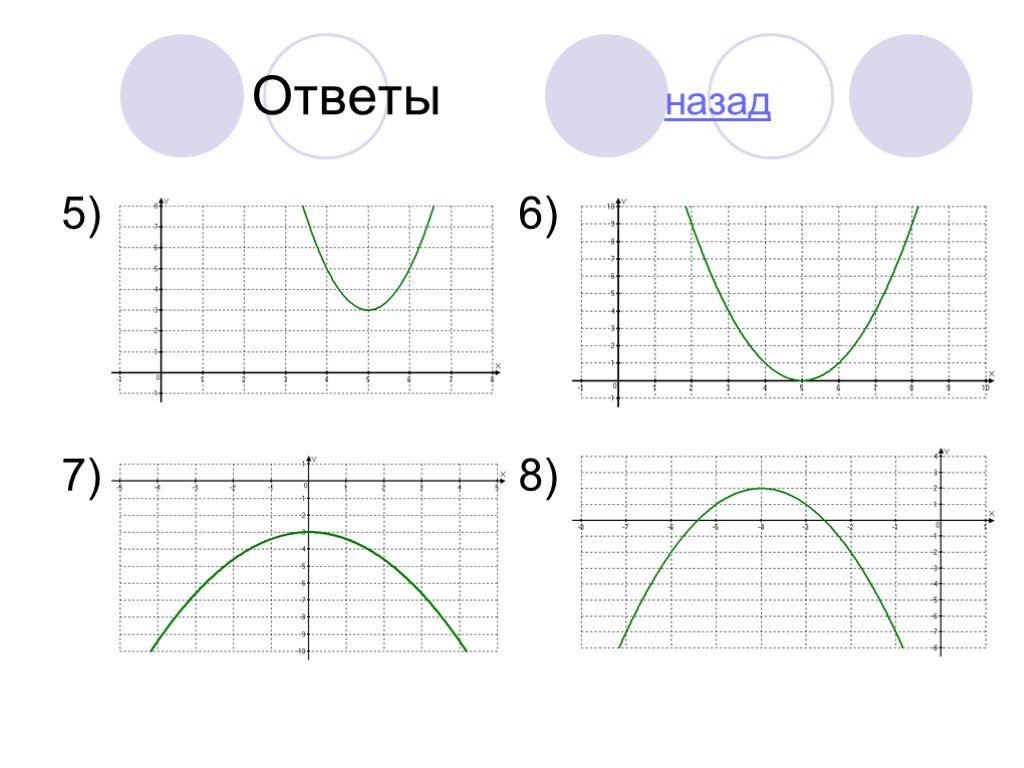
Задание №6 Постройте график функции 1)y=x2-6x+8 2)y=-(x+4)2-9 3)y=0.5x2-7 4)y=2(x+4)2 5)y=2(x-5)2+3 6)y=(x-5)2 7)y=-0.4x2-3 8)y=-x2-8x-14
Перейти к ответам
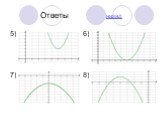
Слайд 39Ответы
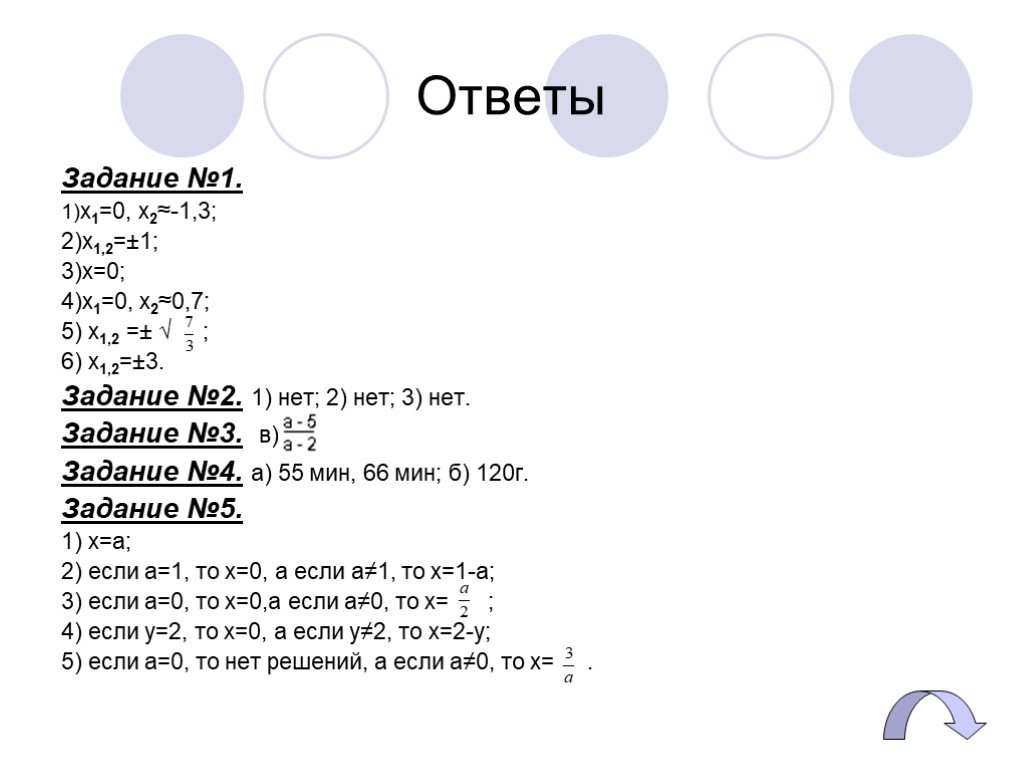
Задание №1. 1)x1=0, x2≈-1,3; 2)x1,2=±1; 3)x=0; 4)х1=0, х2≈0,7; 5) х1,2 =± √ ; 6) x1,2=±3. Задание №2. 1) нет; 2) нет; 3) нет. Задание №3. в) Задание №4. а) 55 мин, 66 мин; б) 120г. Задание №5. 1) x=a; 2) если a=1, то x=0, а если a≠1, то x=1-a; 3) если a=0, то x=0,а если a≠0, то x= ; 4) если y=2, то x=0, а если y≠2, то x=2-y; 5) если a=0, то нет решений, а если a≠0, то x= .
Слайд 40Задание №6 1) 2) 3) 4)
Слайд 41Ответы назад 5) 6) 7) 8)
Слайд 42Заключение содержание
Вопросы о том, как складывались первичные математические представления о квадратных уравнениях, какой вид они принимали, как проходили первые этапы их совершенствования, никогда не теряли своей актуальности и не потеряют ее в будущем. В том, чтобы правильно освещать эти вопросы, заинтересованы весьма широкие слои человеческого общества: и те, кто начинает свое математическое образование; и те, кто учит детей математике, так как это способствует отысканию и использованию наиболее эффективных методических приемов. Предложенная презентация содержит основные понятия, формулы, теоремы, связанные с курсом изучения квадратных уравнений. Для закрепления теоретической части предложен практикум, где рассмотрены примеры уравнений с решением. В заключительной части предложены тесты для самостоятельного закрепления материала.

Слайд 43Список используемой литературы.
Алгебра. Дополнительные главы к школьному учебнику 8 класс. Ю. Н. Макарычев, Н. Г. Миндюк. Москва. «Просвещение» 2003 год. В данном учебном пособии излагается материал, который соответствует программе углубленного изучения математики и выходит за рамки действующих учебников алгебры 8 класса. Этот материал состоится по принципу модульного дополнения действующих учебников и естественным образом примыкает к курсу, углубляет и расширяет его. Алгебра. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы 9 класс. Москва. «Дрофа» 2002 год. Подбор материала по всему разделу курса алгебры. Алгебра. Сборник задач по алгебре для поступающих в вузы. Книга 1. М. И. Сканави. Москва. «ОНИКС 21 век • Мир и образование» 2002 год. Задачи объединены по принципу однородности тем, типов, методов решения и разбиты на три группы по уровню их сложности. Ко многим задачам даны подробные решения. Большая российская энциклопедия. Школьная энциклопедия – математика. С. М. Никольский. Москва. «Дрофа» 1997 год. «Математика» - первая из серии школьных энциклопедий, состоит из 2-х частей: основной и дополнительной, каждая составлена из нескольких разделов, где статьи расположены в алфавитном порядке. В книге имеется биографический указатель. Сборник задач по алгебре 8-9 класс. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич. Москва. «Просвещение» 2002 год. В данном пособии содержаться задачи, способствующие систематическому углублению изучаемого материала и развитию навыков решения сложных задач, а также подготовке к экзаменам. Интернет.