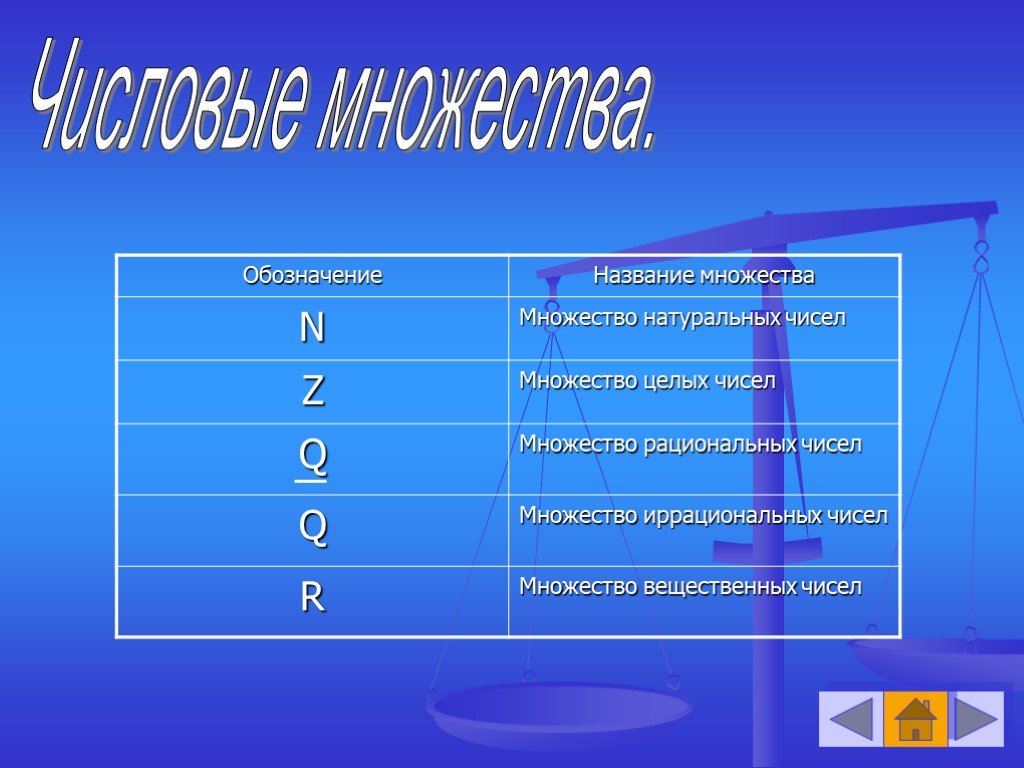
Презентация "Действительные числа" по математике – проект, доклад

Презентация по теме: «Действительные числа».

Выполнила: учитель математики ГОУ СОШ № 457 Ж.Ю. Магаз Санкт-Петербург 2010

Числовые множества.

Множество натуральных чисел.

Натуральные числа - это числа счета. N={1,2,…n,…}. Заметим, что множество натуральных чисел замкнуто относительно сложения и умножения, т.е. сложение и умножение выполняются всегда, а вычитание и деление в общем случае не выполняются

Множество целых чисел.

Введем в рассмотрение новые числа: 1) число 0 (ноль), 2) число (-n), противоположное натуральному n. При этом полагаем: n+(-n)=(-n)+n=0, -(-n)=n. Тогда множество целых чисел можно записать так: Z ={…,-n,…-2,-1,0,1,2,…,n,…}. Заметим также, что: Это множество замкнуто относительно сложения, вычитания и умножения, т.е. Из множества целых чисел выделим два подмножества: 1) множество четных чисел 2) множество несетных чисел

Деление с остатком.

В общем случае действие деления в множестве целых чисел не выполняется, но известно, что деление с остатком можно выполнить всегда, кроме деления на 0. Определение деления с остатком. Говорят, что целое число m делится на целое число n с остатком, если найдутся два числа q и p, такие что: (*) Хорошо известен алгоритм деления с остатком. Замечание: если r=0, то будем говорить, что m делится нацело на n.

m=nq+r, где 0≤ r

ПРИМЕРЫ:

Разделить с остатком m на n. 1). m=190, n=3 190 3 18 6 3 10 9 1 q=63, r=1, 1q=2, r=3 (3

3). m=-15, n=4 По формуле (*): -15=4q+r => q=-4, r=1 -15=4*(-4)+1 4). M=6, n=13 По формуле(*): 6=13q+r =>q=0, r=6 6=13*0+6

Множество рациональных чисел.

Множество рациональных чисел можно представить в виде: В частности, Таким образом, Множество рациональных чисел замкнуто относительно сложения, вычитания, умножения и деления (кроме случая деления на 0).

Но в множестве рациональных чисел нельзя, например, измерить гипотенузу прямоугольного треугольника с катетам . По теореме Пифагора гипотенуза будет равна .Но число не будет рациональным, так как ни для каких m и n. Нельзя решить уравнение . Нельзя измерить длину окружности и т.д. Заметим, что всякое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.

Множество иррациональных чисел.

Числа, которые представляются бесконечной непериодической дробью, будем называть иррациональными. Множество иррациональных чисел обозначим Для иррациональных чисел нет единой формы обозначения. Отметим два иррациональных числа, которые обозначаются буквами – это числа и е.

Число «пи»

Отношение длины окружности к диаметру есть величина постоянная, равная числу

d

Число е.

Если рассмотреть числовую последовательность: с общим членом последовательности то с ростом п значения будут возрастать, но никогда не будет больше 3. Это означает, что последовательность ограничена. Такая последовательность имеет предел, который равен числу е.

Известно, что мощность иррациональных чисел больше мощности рациональных, т.е. Иррациональных чисел «больше», чем рациональных. Кроме того, как бы ни были близки два рациональных числа, между ними всегда есть иррациональное, т.е. Примеры иррациональных чисел: (золотое сечение) и т.д.

Множество вещественных (действительных) чисел.

Множество вещественных чисел – это объединение множества рациональных чисел. Вывод: (см. рис. 1)

Определение модуля вещественного числа

1) Пусть на числовой оси точка А имеет координату а. Расстояние от точки начала отсчета О до точки А называется модулем вещественного числа а и обозначается |a|. 2) Раскрытие модуля происходит по правилу:

|a| = |OA|

Например: Замечание. Определение модуля можно расширить: Пример. Раскрыть знак модуля.

Основные свойства модуля

1) 2) 3) 4) 5) 6)

Решение примеров с использованием свойств модуля

Пример 1. Вычислить Пример 2. Раскрыть знак модуля Пример 3. Вычислить 1) 2) 3)