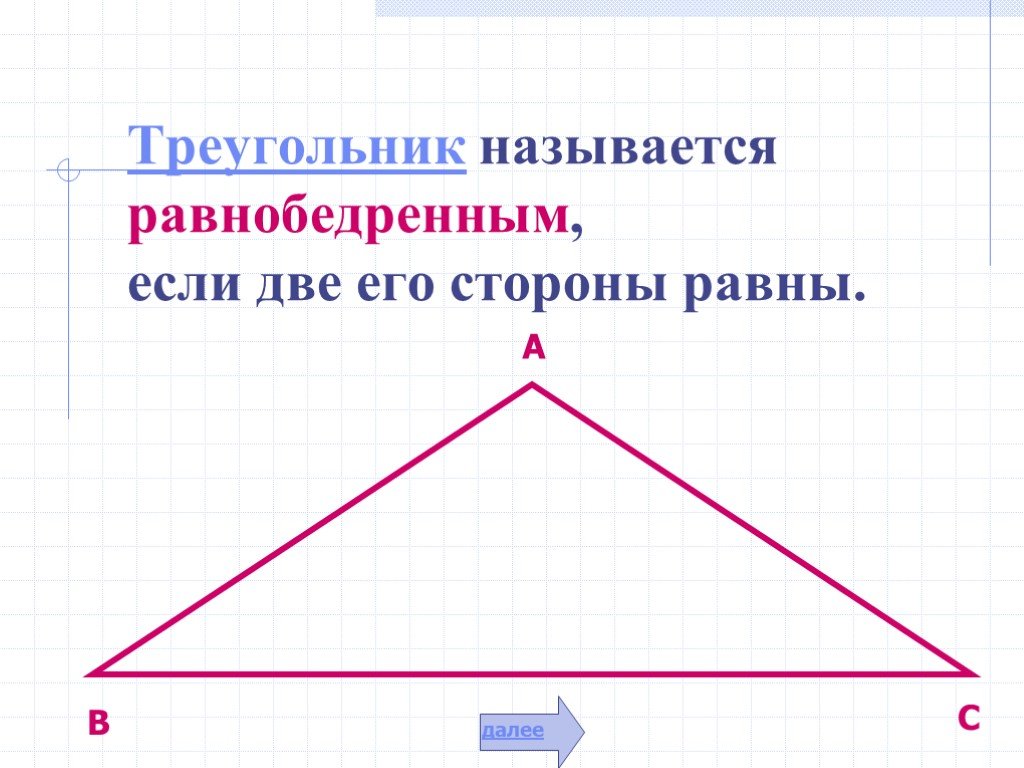
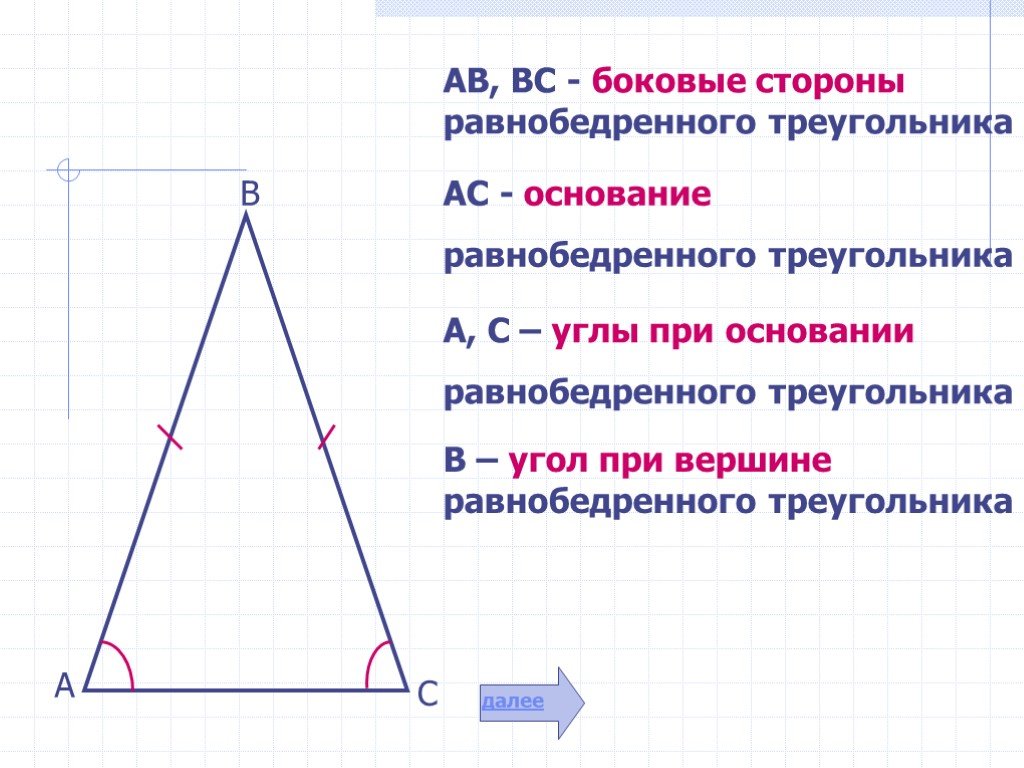
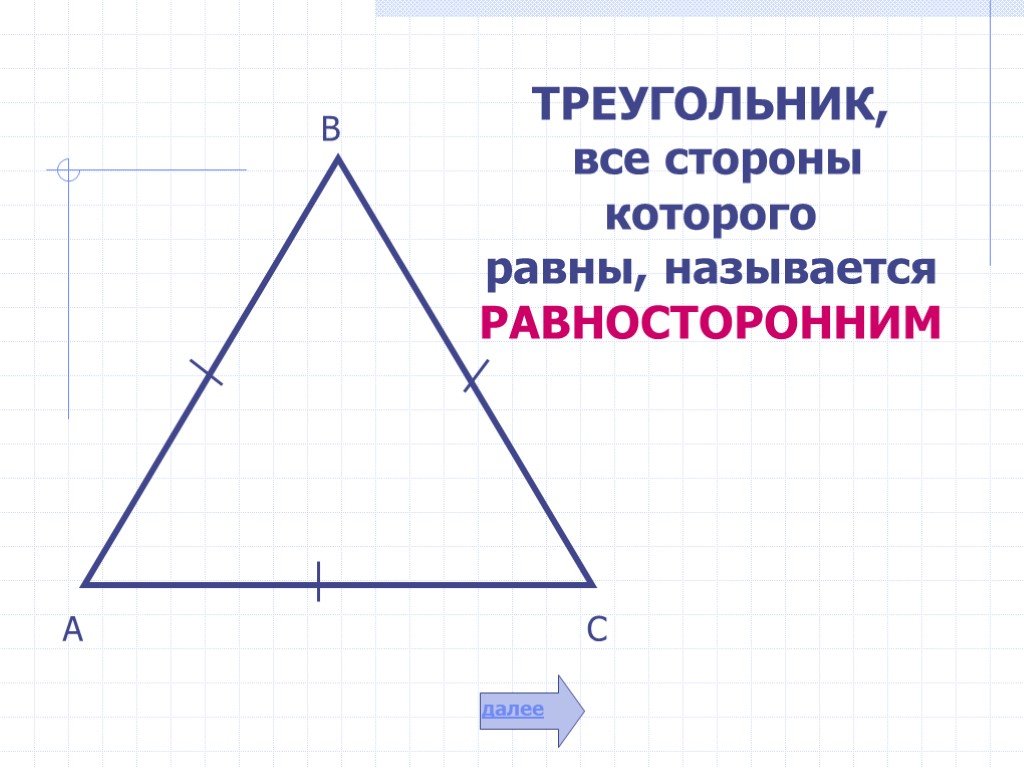
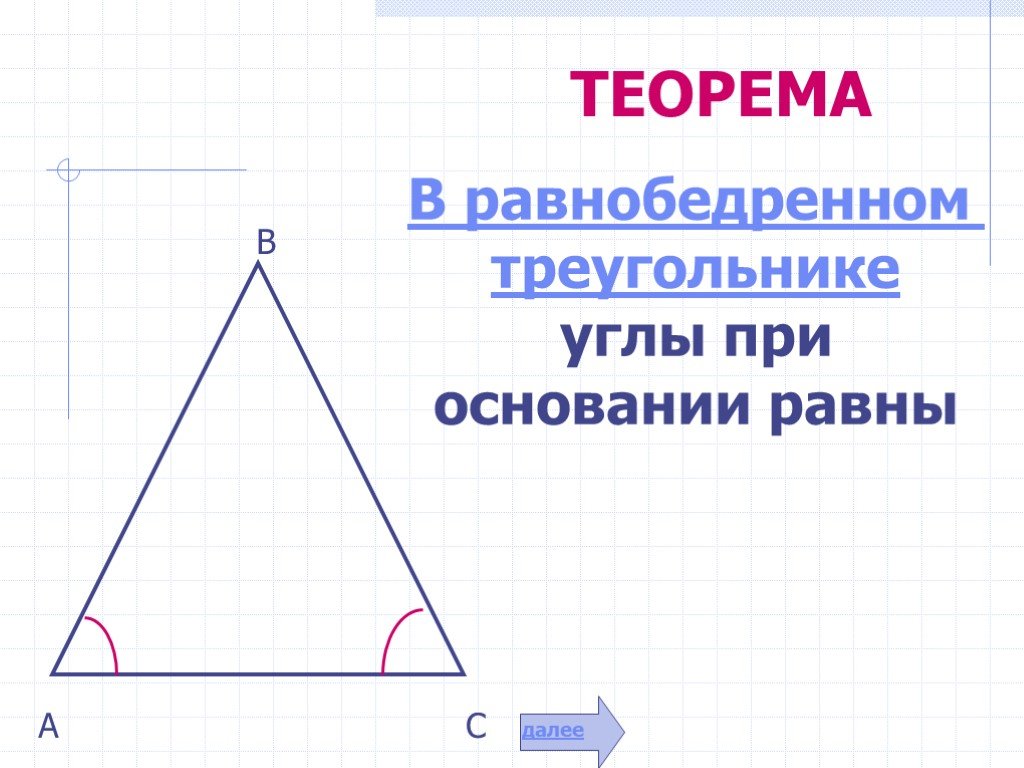
Презентация "Свойства равнобедренного треугольника" по математике – проект, доклад
Презентацию на тему "Свойства равнобедренного треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
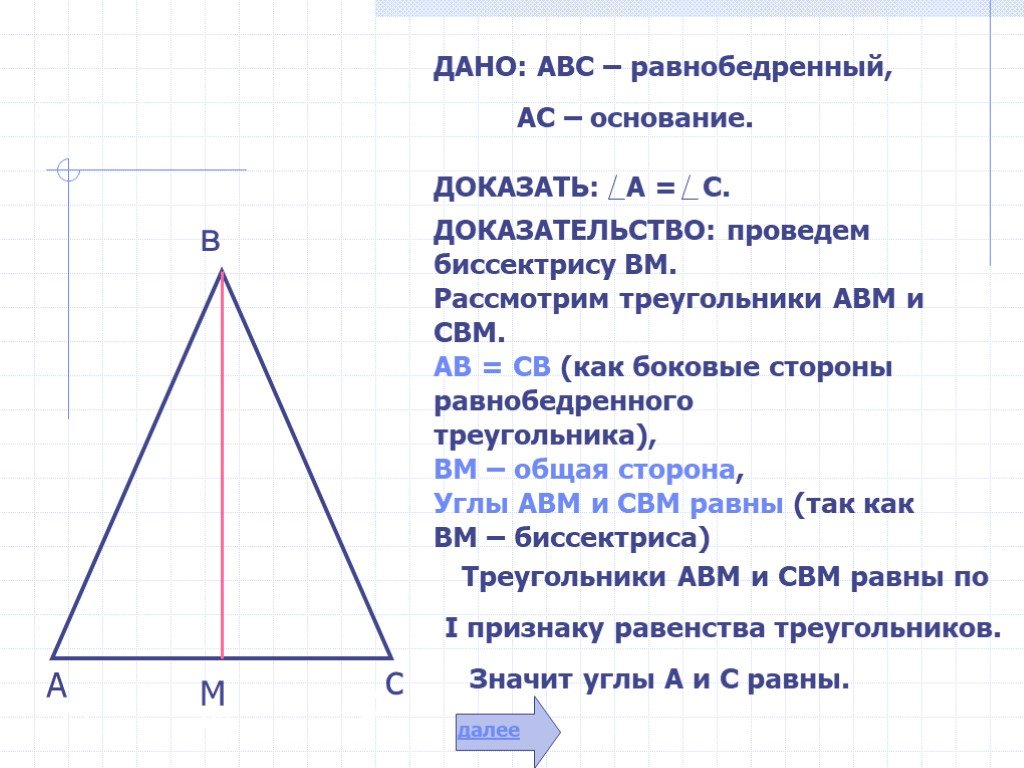
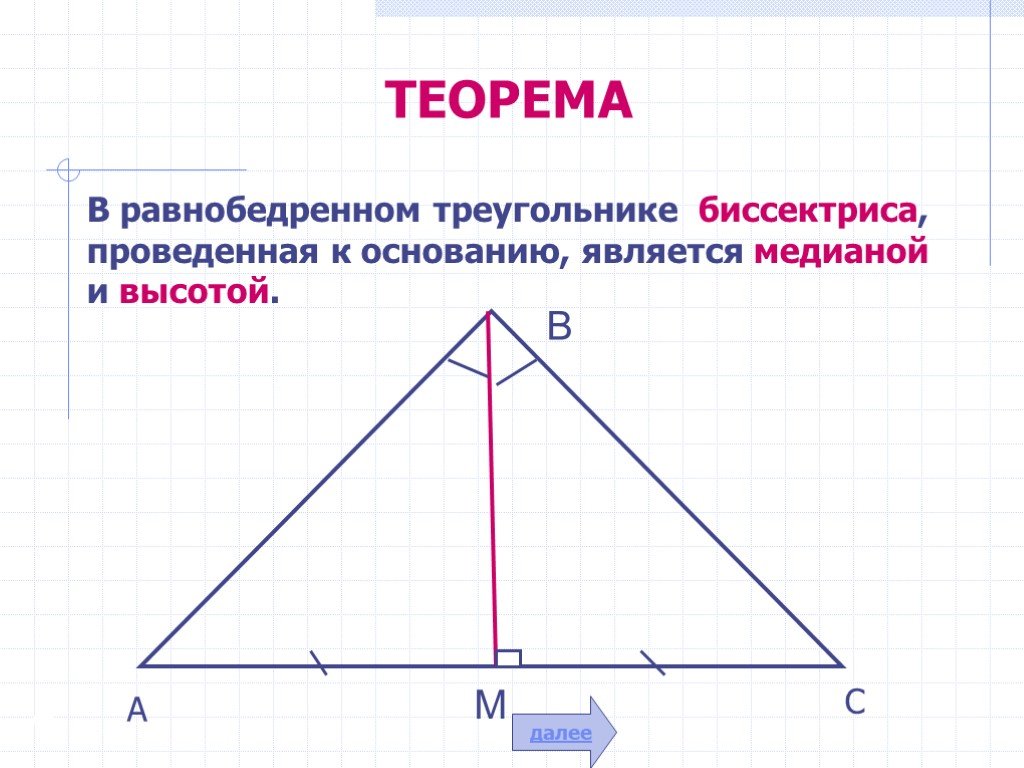
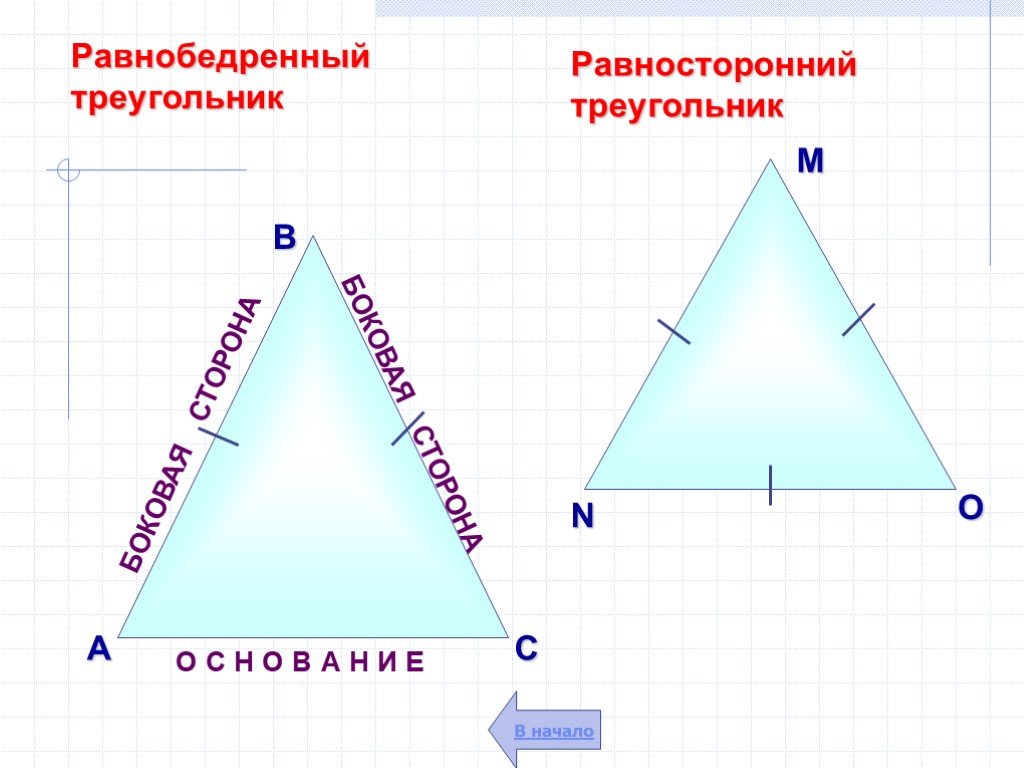
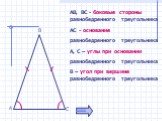
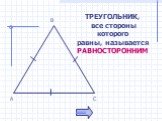
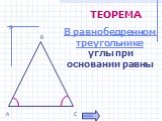
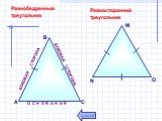
Свойства равнобедренного треугольника
ЦЕЛЬ. пропедевтика стереометрических знаний; развитие пространственного мышления; закрепление признаков и свойств равнобедренного треугольника в новой ...Свойства равнобедренного треугольника
Теоретический опрос. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой. Сформулируйте и докажите теорему ...Свойства равнобедренного треугольника
Тема: «Свойства равнобедренного треугольника». Геометрия – это искусство хорошо рассуждать ... Нильс Г. Абель. Цели урока:. Создать условия для: введения ...Свойства равнобедренного треугольника
план урока:. Решение задач по готовым чертежам Виды треугольников по длинам сторон Доказательство теоремы Решение задач Самостоятельная работа. Решить ...Свойства равнобедренного треугольника
Медиана треугольника. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Биссектриса треугольника. ...Признаки равенства треугольников и свойства равнобедренного треугольника
План работы на уроке:. Признаки равенства треугольников. Свойства равнобедренного треугольника. Вопрос - ответ. 1. Какая фигура называется треугольником? ...Свойства треугольника
Треугольники Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти ...Cвойства равнобедренного треугольника
Медианы, биссектрисы и высоты треугольника. Как называется отрезок ВК на рисунке? ВК - биссектриса АВК = СВК. Сформулировать определение биссектрисы ...Построение равнобедренного треугольника
Задача. Условие: Построить ABC по стороне АС=4см и углу при основании. Дано: АС=4 см Угол α А С А. Построение. Построение: 1) Построить прямую a 2)AC ...Периметр равнобедренного треугольника
х + : - Математические действия I и II ступеней. 06.01.2018 http://aida.ucoz.ru. Треугольник Умножение на 3 Деление на 3 «Волшебное число». Периметр ...Свойства и график функции синус
Устная разминка 1 3 4 5 6 7 8 9 10 11 13 14 15 ☺ cos90° sin90° sin(π/4) cos180° sin270° sin(π/3) cos(π/6) cos360° ctg(π/6) tg(π/4) sin(3π/2) cos(2π) ...Задачи на вычисление площади треугольника
Девиз урока: «Кто ищет – тот всегда найдет…». Личностные цели. самостоятельно добывать знания, анализировать и обобщать; уверенно и грамотно выражать ...Свойства трапеции
Какой четырехугольник называется трапецией? Ответ: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. ...Свойства степени с натуральным показателем
Цели урока. Формирование алгоритмов умножения и деления степеней, возведение в степень выражений. Выработка умения строить графики прямой пропорциональности ...Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Свойства параллельных прямых
Цели урока:. Рассмотреть свойства параллельных прямых. Показать учащимся применение свойств параллельных прямых. Закрепить знания, умения и навыки ...Свойства натурального ряда
ИССЛЕДОВАНИЕ. ИССЛЕДОВАНИЕ Предмет исследования. ИССЛЕДОВАНИЕ Предмет исследования Свойства натурального ряда. ИССЛЕДОВАНИЕ Предмет исследования Свойства ...Логарифмы. Свойства логарифмов
Изобретатель первых логарифмических таблиц, впервые ввёл сам термин «логарифм» шотландский математик Джон Непер. «Я старался, насколько мог и умел, ...Логарифмы. Свойства логарифма
ЛОГАРИФМЫ. Во многих задачах требуется уметь решать уравнения вида a =b. Для этого надо найти показатель степени по данным значениям степени и её ...Косинус острого угла прямоугольного треугольника
Историческая справка. Расположение углов и сторон. А С В b c a. АС – противолежащий катет. ВС – прилежащий катет. ВС - противолежащий катет. АС – ...Конспекты
Свойства равнобедренного треугольника
Коммунальное государственное учреждение. «Школа-лицей №101». акимата города Караганды. . государственного учреждения «Отдел образования города ...Свойства равнобедренного треугольника
План-конспект урока. Класс: 7. Курс: геометрия. Учебник: . Геометрия, 7-9 классы, Л.С. Атанасян. Тема урока: «Свойства равнобедренного треугольника». ...Свойства равнобедренного треугольника
Муниципальное казенное общеобразовательное учреждение. . «Овечкинская средняя общеобразовательная школа. Завьяловского района» Алтайского края. ...Геометрия треугольника
Тема урока:. . «Геометрия треугольника». Тип урока: обобщающий урок по курсу геометрии. . Форма проведения урока: урок - бенефис». Цель урока:. ...Вычитание. Свойства вычитания
Тема урока:. . «Вычитание. Свойства вычитания». Форма урока:. урок «открытия» нового знания с применением ИКТ. Цели урока:. . Деятельностная ...Сумма внутренних углов треугольника
Тема урока. : «Сумма внутренних углов треугольника». Класс:. 7. . Цели урока. :. . Обучающие:. Сформулировать экспериментальным путем вывод ...Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника (8-й класс). Цели:. Совершенствовать. навыки решения прямоугольных треугольников. ...Свойства функций
Конспект урока по алгебре и началам анализа в 11 классе. . . . Учитель математики высшей категории. Юдинцева Валентина ...Свойства тригонометрических функций
Тема: Свойства тригонометрических функций. Цель:. Повторить, закрепить, обобщить свойства тригонометрических функций. Совершенствовать умения и ...Свойства степени с натуральным показателем
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа № 21. город Ставрополь. Конспект ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:22 ноября 2018
Категория:Математика
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию