Презентация "«Теория вероятности»" (9 класс) по математике – проект, доклад
Презентацию на тему "«Теория вероятности»" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 31 слайд(ов).
Слайды презентации
Список похожих презентаций
«Основы теории вероятности»
В современном мире автоматизации производства теория вероятности(Т.В) необходима специалистам для решения задач, связанных с выявлением возможного ...Математическая статистика и теория вероятности
Группы и специальности потоков. 92... Электроэнергетические системы и сети (100200) - 140205 93... Электроснабжение (100400) - 140211 94... Релейная ...Теория вероятности в школе
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. Знание закономерностей, которым подчиняются массовые случайные ...Теория вероятности и статистика
Вероятность и статистика. Вероятностно-статистические закономерности изучает специальный раздел математики – теория вероятности. Теория вероятностей ...Теория вероятности и статистика
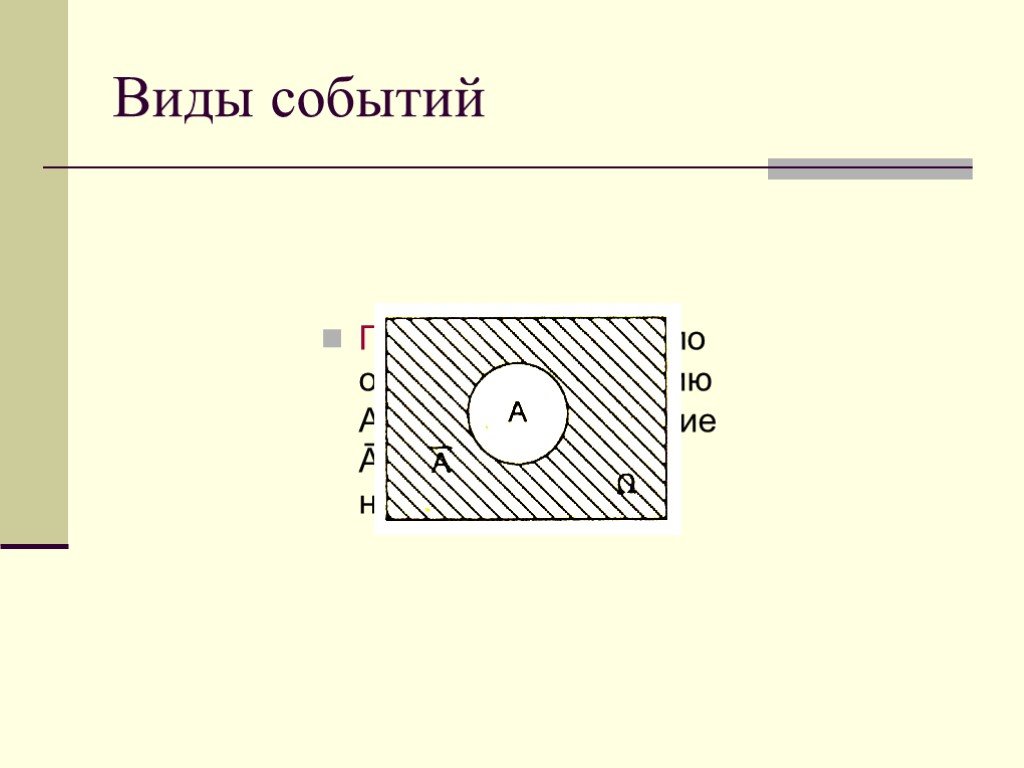
Определение. Пусть А и В – два события, относящиеся к одному случайному опыту. Взяв все элементарные события, которые благоприятствуют и событию А, ...Теория вероятности события
Введение в комбинаторику. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать ...Комбинаторика и теория вероятности
Комбинаторика. «комбинаторика» происходит от латинского слова combinare – «соединять, сочетать». Определение. Комбинаторика – это раздел математики, ...Теория вероятности
Автор проекта ученица 10 класса «А» ГОУ СОШ № 420 г. Москвы Лавренова Юлия Руководитель проекта учитель математики ГОУ СОШ № 420 г. Москвы Афанасьева ...Классическая теория вероятности
Актуальность. Актуальность изучения данной темы заключается в том, что некоторые задачи, которые ставит перед нами реальная жизнь нельзя решить без ...Определение вероятности
При классическом определении вероятность события определяется равенством Р(А) = m/n, где m – число элементарных исходов испытания, благоприятствующих ...Окружность и круг: теория и практика
Цель уроков: ввести понятия окружности и круга, разобрать связанные с ними понятия и формулы , отработать это на задачах и проверить степень усвоения ...Арифметическая теория действительных чисел по Мерэ-Кантору
Георг Кантор (3 марта 1845г. – 6 января 1918г.). Георг Фердинанд Людвиг Филипп Кантор родился 3 марта 1845 г. в России, в Санкт-Петербурге. Его мать, ...ГИА 2013. Модуль алгебра №1
Модуль «Алгебра» №1. Повторение (1). Найдите значение выражения 0,5 ∙ 0,05 ∙ 0,005 . Ответ: 0,000125 0,5 ∙ 0,05 ∙ 0,005 = 1 + 3 6 000 =0,. Повторение ...ГИА 2013. Модуль алгебра №3
Модуль «Алгебра» №3. Наибольшее число :. Повторение (4). Укажите наибольшее из чисел:. Ответ: ⎕ ⎕ ⎕ ⎕. Повторение (подсказка). Чтобы сравнить выражения, ...Реляционная алгебра – механизм манипулирования реляционными данными
Две группы операций РА. теоретико-множественные операции специальные реляционные операции. Теоретико-множественные операции. объединения отношений; ...Понятие вероятности
Статистическое определение вероятности. Вероятность как предельное значение частоты. Самостоятельная работа. Ошибка Даламбера. Великий французский ...Классическое определение вероятности
Цель урока: Выработать умение решать задачи на определение классической вероятности с использованием основных формул комбинаторики. Оборудование: ...Исследование жизненных ситуаций с помощью классического определения вероятности и решение простейших задач
Цель – научить учащихся вычислять вероятности в задачах, описывающих жизненные ситуации Задачи : знакомство с языком теории вероятностей; рассмотрение ...История теории вероятности
Человечество всегда стремилось к некоторого рода предсказаниям. Любая наука основана на этом. Однако предвидение фактов не может быть абсолютным, ...Задачи по вероятности
Номера задач № 1104 № 1105 № 1106 № 1107 № 1108 № 1109 № 1110 № 1111 № 1112 № 1113 № 1114 выход. В колоде 36 карт, из них наугад вынимают одну карту. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 сентября 2018
Категория:Математика
Классы:
Содержит:31 слайд(ов)
Поделись с друзьями:
Скачать презентацию