Презентация "Теорема косинусов" (9 класс) по математике – проект, доклад
Презентацию на тему "Теорема косинусов" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
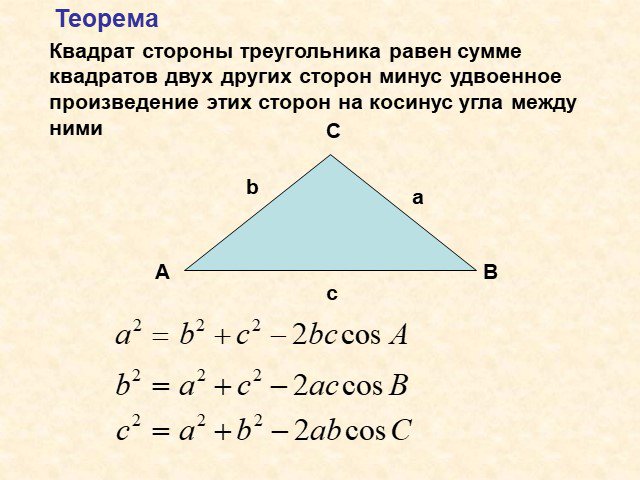
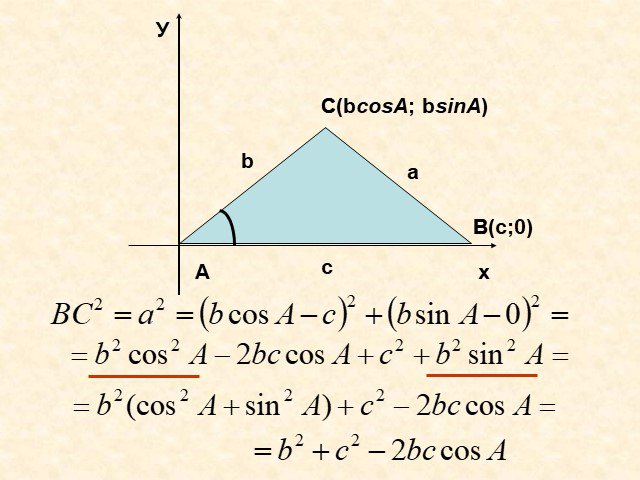
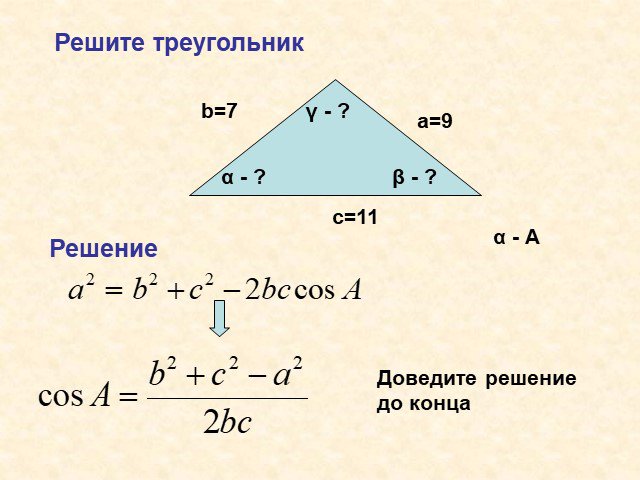
Теорема косинусов
Содержание. Теорема косинусов. Дополнительная информация. Доказательство. Следствие. Пользуемся теоремой косинусов в решение треугольников. Вывод. ...Теорема косинусов в электронных таблицах
Да, путь познания не гладок! Но знаем мы со школьных лет Загадок больше, чем отгадок И поискам предела нет! Пифагор. Цель урока: отработать умения ...Теорема косинусов для треугольника
Цель —. сформулировать теорему косинусов через решение задач, научиться использовать ее при решении задач, в том числе практического характера. 6. ...Теорема косинусов. Следствия из теоремы косинусов
Проверка домашнего задания. №1 Определите вид треугольника заданного своим сторонами 17, 8,15. Решение: Наибольший угол лежит против стороны, равной ...Теорема косинусов
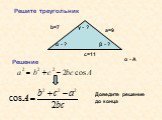
С А В АВ2 = АС2 + ВС2. Теорема косинусов К М ? СЛОЖЕНИЕ. правило треугольника. правило параллелограмма. ВЫЧИТАНИЕ 1 2 3. Формулировка: Квадрат любой ...Теорема синусов и косинусов в задачах с практическим содержанием
Цели урока:. 1) выработать умения и навыки решения задач с практическим содержанием, применяя теоремы; 2) показать связь теории с практикой; 3) продолжать ...Теорема синусов и теорема косинусов
Экскурс в историю Сформулировать и доказать теорему синусов Сформулировать и доказать теорему косинусов Научиться применять данные теоремы к решению ...Теорема синусов, теорема косинусов
Определить вид треугольника (остроугольный, прямоугольный, тупоугольный). Стороны треугольника равны 3,4,5 см Стороны треугольника равны 5, 12,13 ...Теорема Пифагора
Цель. Обобщить и систематизировать знания учащихся по теме, показать исторические истоки теоремы, учить учащихся применять полученные знания к решению ...Теорема Виета
Основная цель – изучить теорему Виета и ей обратную, уметь применять при решении квадратных уравнений. «Вся математика – это, собственно, одно большое ...Теорема синусов
Проверка домашнего задания. № 1020 (а, в) Ответы: в) а). Решение: а) в). Устная работа:. Ответы к задачам по чертежам:. Рис. 174 S = 12. Рис. 176 ...Теорема Пифагора. история, доказательства, применение
Содержание. Введение История теоремы Неалгебраические доказательства теоремы Алгебраические доказательства теоремы Применение теоремы Заключение Литература. ...Теорема Пифагора и ее применение при решении задач
Цель урока:. Повторить теорему Пифагора; Применять теорему Пифагора при решении простейших задач геометрии; Рассмотреть исторические задачи; Рассмотреть ...Теорема Пифагора для треугольника
Теорема Пифагора. Легенды и факты о Пифагоре. Авторы презентации : Власенко Д., Белохвостова Т., Слизкова П., Матвеева П., Муравьева А. Пифагорейская ...Теорема Пифагора 7-9 класс
Тема проекта Теорема. Творческое название проекта «Истина где-то рядом...». Участники проекта: Андриянов Станислав Носова Ксения. Пифагора. Дидактические ...Площади фигур. Теорема Пифагора
Установите соответствие между фигурой и формулой площади. . Задача № 1. В треугольнике два угла равны 45 и 90 , а большая сторона 12 см. Найдите 2 ...Теорема Виета
Заполнить таблицу. 3 5 6 -3 -4 -7 -1 4 -5 1 -6. Теорема Виета. Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому ...Теорема Виета
Теорема Виета Цели урока:. Доказать теорему Виета. Научится решать квадратные уравнения применяя теорему Виета. Рассмотреть свойства коэффициентов ...Теорема Виета
Решим уравнение:. Как называется квадратное уравнение такого вида? Приведенное Чему равна сумма и произведение корней данного уравнения? 5+2=7 и 5*2=10 ...Теорема Гельмгольца
Вывод уравнения неразрывности. . . . . . Первая и вторая формулы Грина. . . . . . . Теорема Гельмгольца (о разложении векторного поля). . . . . ...Конспекты
Теорема Пифагора и её применение
МКОУ Новониколаевская СОШ. Барабинского района. Новосибирской области. Урок - путешествие в 8 классе по теме:. «Теорема Пифагора и её применение». ...Теорема Пифагора
Конспект урока для 8 класса «. Теорема Пифагора». Класс:. 8. Цели урока:. Организовать деятельность учащихся по применению теоретических знаний ...Теорема Пифагора
Государственное бюджетное образовательное учреждение г.Москвы. . средняя общеобразовательная школа №1968. Урок для 8 класса по теме ...Теорема Пифагора
Тема урока по геометрии в 8-м классе: "Теорема Пифагора». Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора ...Теорема Пифагора
План – конспект урока геометрии в 8 классе. по теме «Теорема Пифагора». Учитель: Платонова Валентина Николаевна. Цель урока. : изучить доказательство ...Теорема Ферма, теорема Роля, теорема Лагранжа, теорема Коши
Тема урока:. Теорема Ферма, теорема Роля, теорема Лагранжа, теорема Коши. Тип урока:. Урок изучения нового материала. Цель урока:. Обучающая:. ...Теорема Пифагора
Урок геометрии в 8-м классе: "Теорема Пифагора". Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора и ее применение ...Теорема Виета
Урок по алгебре в 8 классе по теме «Теорема Виета». Конева Надежда Александровна, учитель математики ВКК. . МБОУ Борисоглебского городского округа. ...Теорема Виета
Урок алгебры в 8 классе Учитель: Барсукова Н.А. Тема урока:. Теорема Виета. Тип урока:. открытие новых знаний. Технология:. проблемно – ...Теорема Безу и следствие из неё
Муниципальное бюджетное общеобразовательное. . учреждения гимназия № 19 им.Н.З.Поповичевой. . г.Липецка. Урок алгебры по теме:. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:26 октября 2015
Категория:Математика
Классы:
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию