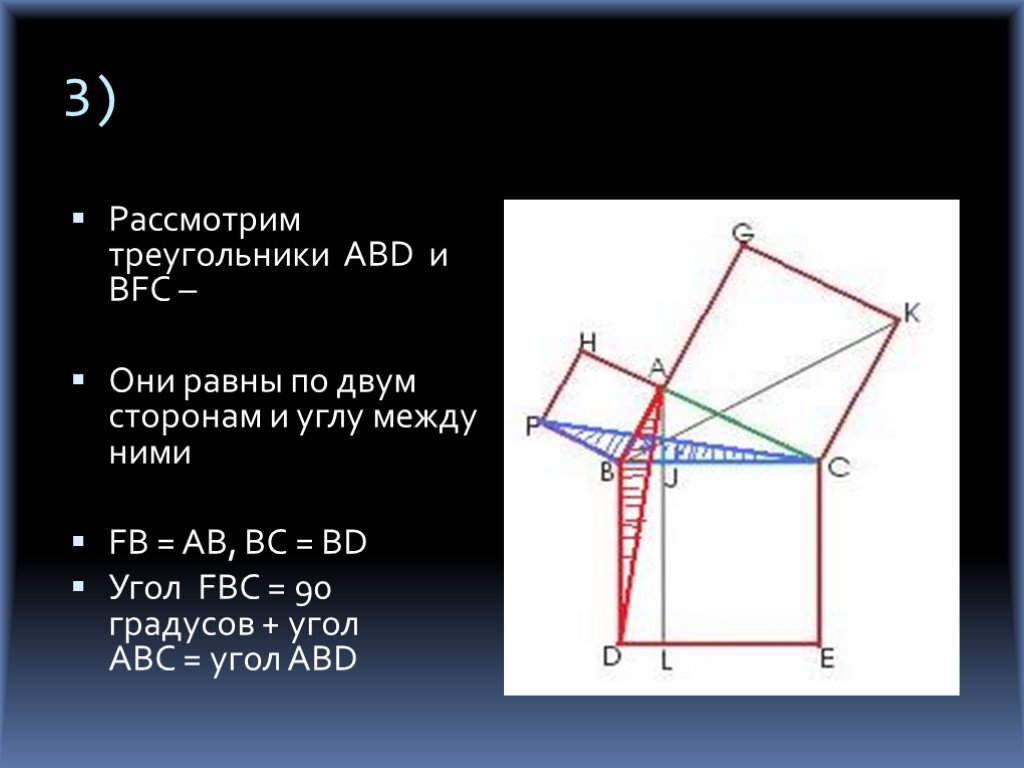
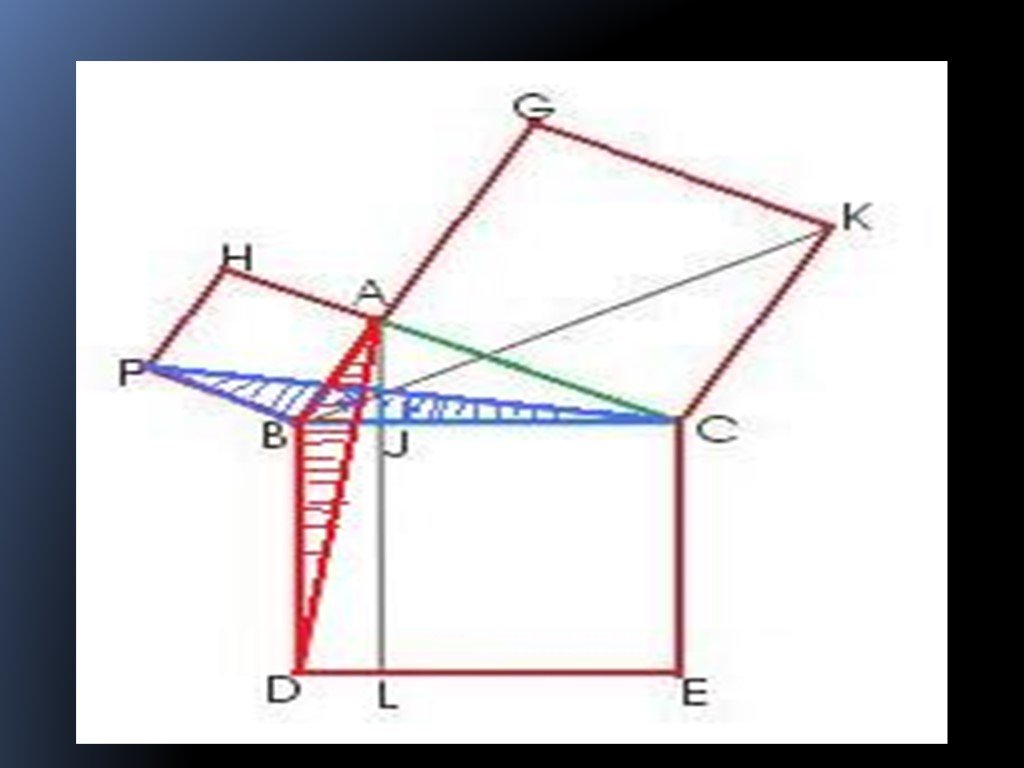
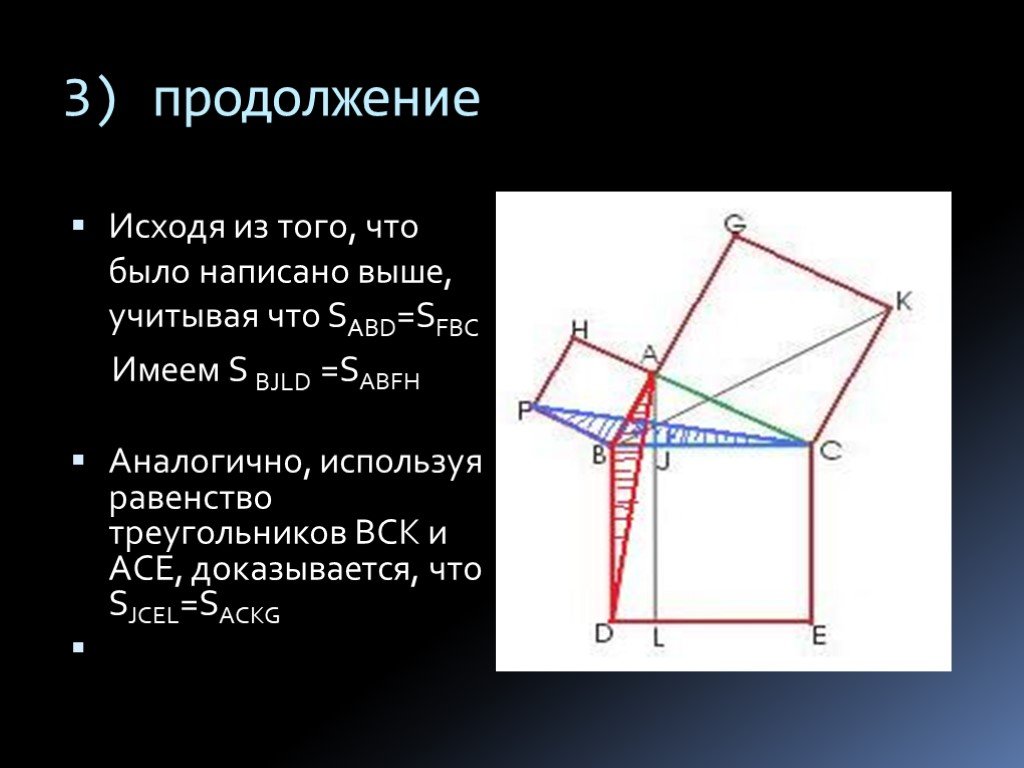
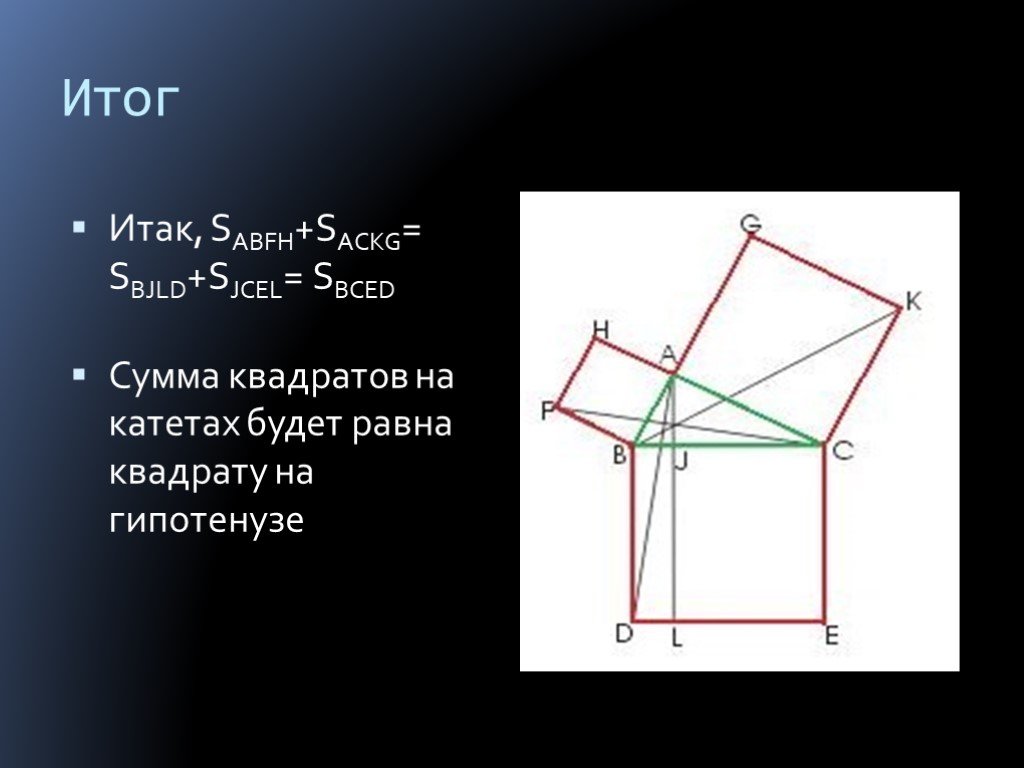
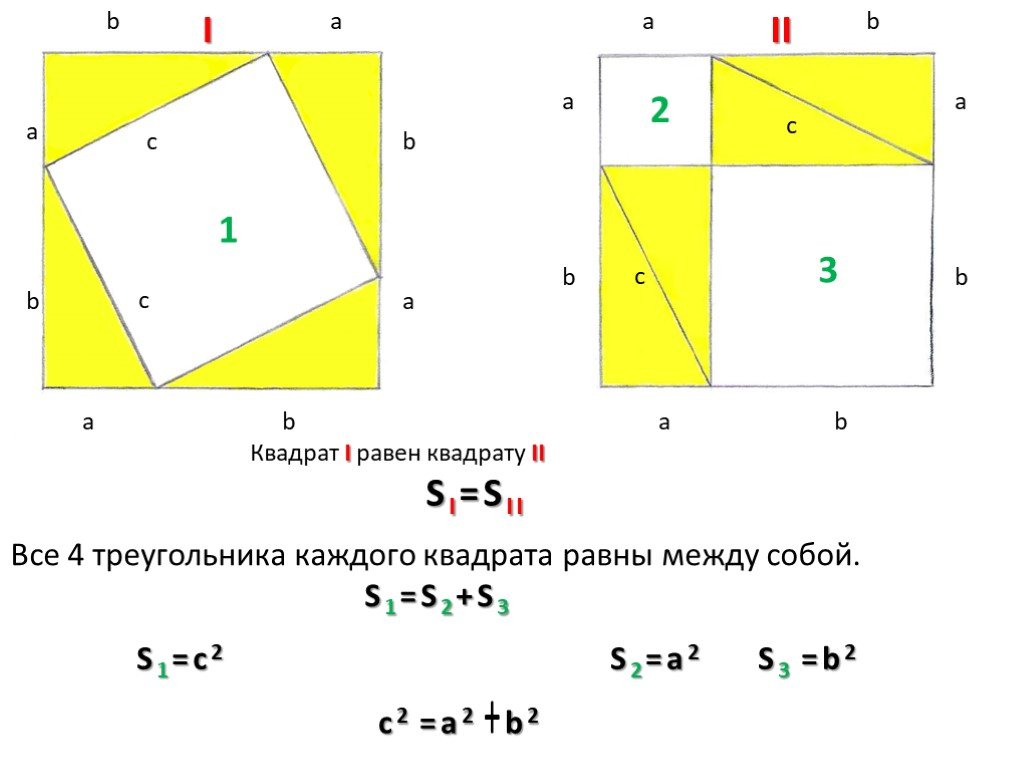
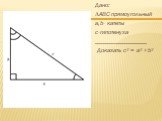
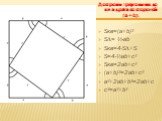
Презентация "Теорема Пифагора для треугольника" по математике – проект, доклад
Презентацию на тему "Теорема Пифагора для треугольника" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 43 слайд(ов).
Слайды презентации
Список похожих презентаций
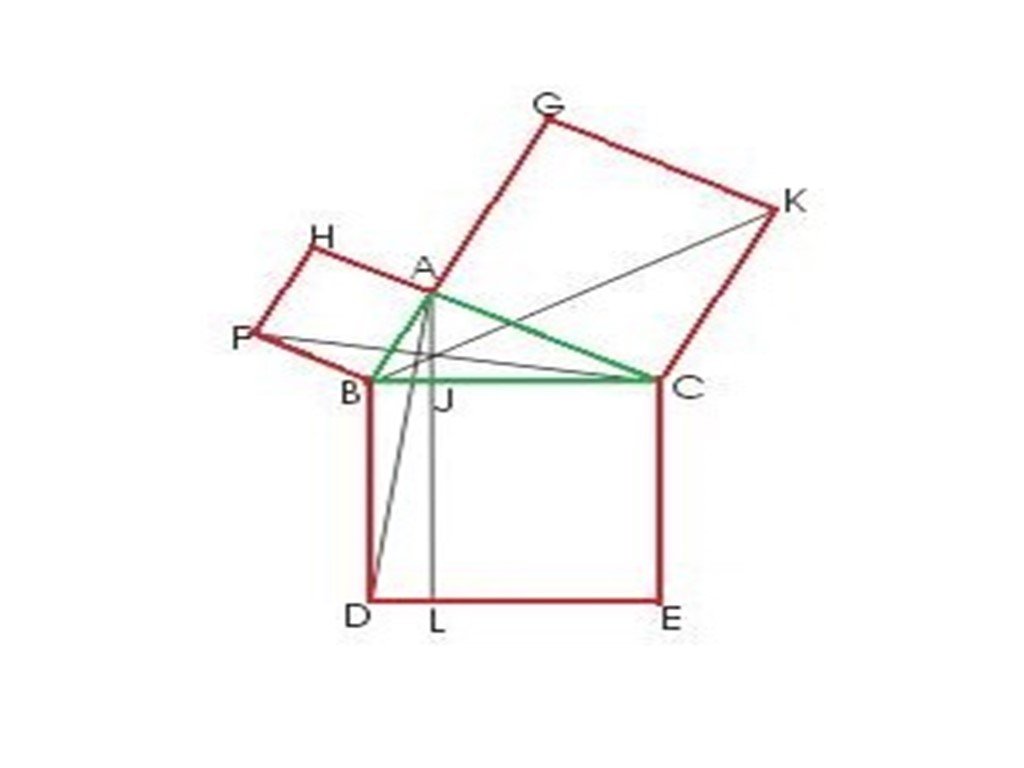
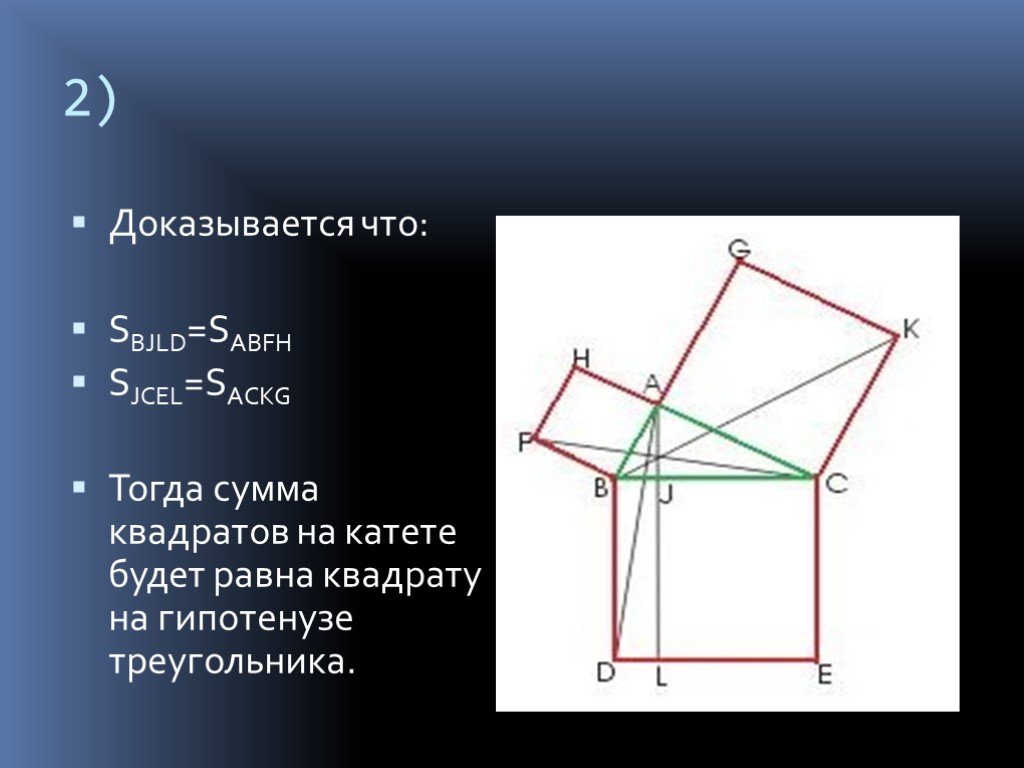
Многоликая теорема Пифагора
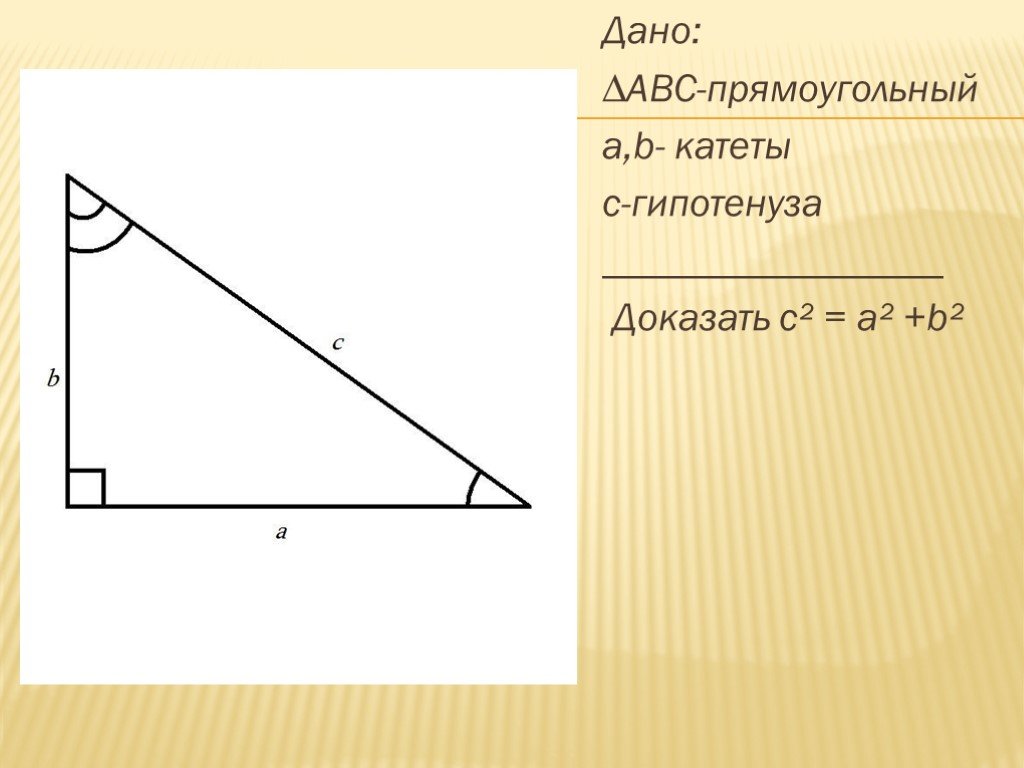
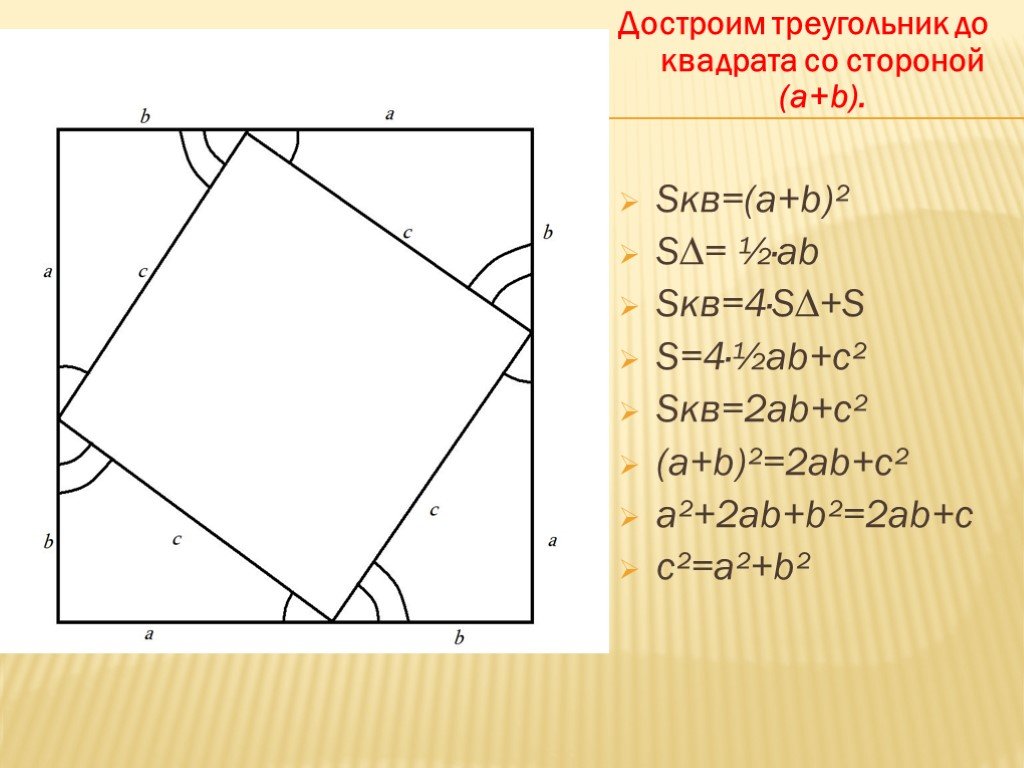
Аннотация. На протяжении многих лет людей интересовал вопрос о теореме Пифагора и о различных способах её доказательства. Причина такой популярности ...От египетского треугольника до Пифагора
Древний Египет. В 23 веке до н.э. был известен прямоугольный треугольник со сторонами 3,4,5.Это единственная тройка последовательных чисел, для которых ...Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач
Объект исследования: Теорема Пифагора и пифагоровы тройки. Предмет исследования: Применение пифагоровых троек для быстрого решения геометрических ...Пространственная теорема Пифагора
Все плоские углы тетраэдра ОABC при вершине О — прямые. Докажите, что квадрат площади треугольника ABC равен сумме квадратов площадей остальных граней ...Внешний угол треугольника. Теорема о внешнем угле треугольника
I. Cумма углов треугольника. 1. На доске доказать теорему о сумме углов треугольника: Сумма углов треугольника равна 1800 2. Решить задачу № 749 (чёт ...Площади фигур. Теорема Пифагора
Установите соответствие между фигурой и формулой площади. . Задача № 1. В треугольнике два угла равны 45 и 90 , а большая сторона 12 см. Найдите 2 ...Ребусы для 5 класса
1. ответ защелка. 2. модель. 3. опять. 4. пятнашки. 5. Родина. 6. осень. Разгадай сам Эти ребусы. . . . . . . 7. 8. А как вам такой вид ребуса? А ...Признаки равенства треугольников и свойства равнобедренного треугольника
План работы на уроке:. Признаки равенства треугольников. Свойства равнобедренного треугольника. Вопрос - ответ. 1. Какая фигура называется треугольником? ...Вводное повторени для 8 классов по геометрии
8 9 10 11 14 15 16 17 18 30 33 34 35 36 1 3 4 5 6 13 19 31 7. Найти: 440 D С О В А ? 2. Дано:. a0 F b0. O. N R M L. a b c 650. . 450 K E 1350 800. ...Вклад Пифагора в развитие музыки
В Древней Греции была впервые замечена некая закономерная связь между звуками и математическими величинами. Открытие этих закономерностей связано ...Построение треугольника по трем элементам
Построение треугольника по трем элементам. 1 вариант - построение треугольника по двум сторонам и углу между ними. 2 вариант - построение треугольника ...Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Вопросы для повторения:. Пропорциональные отрезки: 1. Высота, проведённая из вершины прямого угла на гипотенузу в прямоугольном треугольнике, делит ...Cвойства равнобедренного треугольника
Медианы, биссектрисы и высоты треугольника. Как называется отрезок ВК на рисунке? ВК - биссектриса АВК = СВК. Сформулировать определение биссектрисы ...Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Теорема 2. В произвольном треугольнике против большей стороны лежит больший угол. Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны ...Внешний угол треугольника
Треугольник (музыкальный инструмент). Жесткость треугольников. Бермудский треугольник. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. У треугольника может быть два тупых ...Внеклассное мероприятие по математике для учащихся 6-х классов
“Рыбе – вода, птице – воздух, зверю – лес, степи, горы. А человеку нужна Родина. И охранять природу – значит охранять Родину”. М.М. Пришвин. Наша ...Внетабличное умножение и деление. Приём деления для случаев вида 782, 693
22 января. Классная работа. 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8. Устный счет. 1. А) Уменьшаемое, вычитаемое, разность. Б) Множитель, множитель, произведение. ...Внеклассное мероприятие по математике для учащихся 6 -ов
Цель внеклассного мероприятия:. 1. Повышение интереса к изучению математики, развитие творческих способностей учащихся и логического мышления. 2. ...Внеклассное мероприятие по математике для 8 класса Отличники
1. Способствование проявлению интеллектуальных способностей учащихся. 2. Активизации познавательной деятельности учащихся. 3. Формирование навыков ...Вневписанная окружность треугольника
Вневписанная окружность. B A C Ka K1. Kb Kc ra rb rc. Определение. Вневписанной окружностью треугольника называется окружность, касающаяся одной из ...Конспекты
Теорема Пифагора и её применение
МКОУ Новониколаевская СОШ. Барабинского района. Новосибирской области. Урок - путешествие в 8 классе по теме:. «Теорема Пифагора и её применение». ...Теорема Пифагора. Различные способы доказательства
ПЛАН-КОНСПЕКТ УРОКА. . «Теорема Пифагора. Различные способы доказательства.». . ФИО (полностью). . Поддуева Елена Вадимовна. . ...Теорема Пифагора. Перпендикуляр и наклонная
Тема: «Теорема Пифагора. Перпендикуляр и наклонная». . Автор – Овденко Галина Александровна. . Тест по теме для 8 класса. . . . . ...Теорема Пифагора
Государственное бюджетное образовательное учреждение г.Москвы. . средняя общеобразовательная школа №1968. Урок для 8 класса по теме ...Теорема Пифагора
Урок по геометрии по теме: «Теорема. Пифагора». Подготовила: Сеитова Лариса Ромазановна, учитель математики муниципального казённого общеобразовательного ...Теорема Пифагора
Конспект урока для 8 класса «. Теорема Пифагора». Класс:. 8. Цели урока:. Организовать деятельность учащихся по применению теоретических знаний ...Теорема Пифагора
Тема: Теорема Пифагора. «Кто смолоду делает, думает сам. тот становится потом надежнее. крепче, умнее ». В. Шукшин. Цель обучения :. ...Теорема Пифагора
План – конспект урока геометрии в 8 классе. по теме «Теорема Пифагора». Учитель: Платонова Валентина Николаевна. Цель урока. : изучить доказательство ...Теорема Пифагора
План-конспект урока по теме «Теорема Пифагора» . Цели урока:. . . Изучить некоторые исторические сведения о Пифагоре и его теореме, доказательство ...Теорема Пифагора
Тема урока по геометрии в 8-м классе: "Теорема Пифагора». Цели урока:. Образовательная:. обеспечить понимание доказательства теоремы Пифагора ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:43 слайд(ов)
Поделись с друзьями:
Скачать презентацию