Презентация "Лабораторный практикум по решению некоторых задач математики" по математике – проект, доклад
Презентацию на тему "Лабораторный практикум по решению некоторых задач математики" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 27 слайд(ов).
Слайды презентации
Список похожих презентаций
Бинарный урок математики и природоведения по теме "Итоговое повторение"
Итоговое повторение. Ну-ка, проверь дружок, Ты готов начать урок? Всё ль на месте, Всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...«Олимпийский» задачник по математике
Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи — решайте их Д. Пойа. Если мы действительно что-то ...Башни Кремля. Задачи по математике
Башни Кремля. Спасская башня считается самой красивой и стройной башней. Построена в 1491 году под руководством архитектора Пьетро Антонио Солари ...Веселый урок математики (повторение)
Выбираем название командам. «Пифагорчики» «Цифирята». Сколько хвостов у семи котов? Сколько носов у двух псов? Сколько пальчиков у четырех мальчиков? ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Задачи по математике»
Успех каждого – это шаг к успеху всего класса. Реши примеры 5 ·8 5·5 4·6 8·8 25-5 36-6. 48-8 99-9 6·10 50·10 4·10 7·100. =40 =25 =24 =64 =20 =90 =60 ...Ассоциация, как помощник, при изучении математики
Ассоциация- это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ...Авторалли по городам математики
Цель: Закрепить навык выполнения действий, возведения чисел в квадрат и куб, закрепить формулы пути и площади. Расширение кругозора учащихся, развитие ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...«Решение задач по математике»
10 февраля. В классе. Задача условие вопрос решение ответ. Быстро и правильно считать. Правильно записывать решение задачи. Кричать и сердиться, когда ...Веселые задачки по математике
Задача 1. Попугай, удав и мартышка вместе съели 50 бананов. Попугай съел 3 банана. Сколько процентов всех бананов съел попугай? Задача 1. Решение. ...Гендерная статистика ЕГЭ по техническим предметам
Актуальность: в настоящее время Россия нуждается в кадрах промышленной и строительной областях, в которых трудятся в основном мужчины. Цель: выяснить ...ВСЁ по обыкновенным дробям
9.9.17 Содержание. Повторим Основное свойство дроби Сокращение дробей Приведение дробей к общему знаменателю Сравнение дробей Сложение и вычитание ...Вопросы для знатоков математики
. Правило умножения обыкновенных дробей. Правило умножения смешанных чисел. Правило сложения дробей с разными знаменателями. Правило сложения смешанных ...Внеклассное мероприятие по математике в 8 классе.
I. БЛИЦ-ЗНАКОМСТВО. КАЖДОЙ ИЗ КОМАНД БУДЕТ ЗАДАНО ПО 15 ВОПРОСОВ. ЗА КАЖДЫЙ ПРАВИЛЬНЫЙ ОТВЕТ КОМАНДА ПОЛУЧАЕТ 1 БАЛЛ. ВОПРОСЫ ДЛЯ ПЕРВОЙ КОМАНДЫ. ...Внеклассное мероприятие по математике
школьная жизнь. Предметная неделя естественно-математического цикла. Срок проведения с 13.02.2012 по 20.02.2012 года. Утром 16 февраля на дверях кабинетов ...«Математика» – новый учебник математики
«Математика» – новый учебник математики. Образовательная система «Школа 2100». Цель Принципы Технология. Авторы Образовательной системы Школа 2100. ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Конспекты
Деление и умножение на однозначное число. Решение задач с использованием экологических понятий и терминов
Полякова Елена Александровна. учитель начальных классов. НОУ «Школа – интернат №8 ОАО «РЖД». УРОК . МАТЕМАТИКИ. (3. класс). Тема. : «. ...Дополнение условия задачи. Решение задач
Конспект урока по математике для 1 класса по УМК 21 век. ТЕМА. :. «Дополнение условия задачи. Решение задач». ЦЕЛИ:. 1. Учить выделять части задачи, ...Деление двузначного числа на однозначное. Решение арифметических задач
. УРОК 15 (задания 87-93). . . Учебный предмет:. математика. Класс:. 3. . Авторы учебника:. . Истомина Н.Б., Редько З.Б., Иванова И.Ю. УМК ...Вычитание из чисел 8, 9. Решение задач
КРАСНОПАХАРЕВСКАЯ ООШ – ФИЛИАЛ МБОУ «НОВАДЕЖДИНСКАЯ СОШ». Урок математики для 1 класса по теме: «Вычитание из чисел 8, 9. Решение задач». . Автор: ...Действия с составными именованными числами. Решение задач различного вида
Урок математики в 4 классе. . По программе «Школа 2100». Тема урока:. “Действия с составными именованными числами. Решение задач различного вида. ...Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач
. ТЕМА: «. Деление двузначного числа на однозначное и двузначное число, деление чисел с остатком, решение задач». . Сухова Т.А. . ...Животноводство в нашем крае. Решение задач на движение
Муниципальное общеобразовательное учреждение. «Туендатская основная общеобразовательная школа». Первомайского района Томской области. ...В стране математики
. . Муниципальное казенное дошкольное образовательное учреждение. «Детский сад компенсирующего вида №7 «Сказка». . . Конспект урока ...Деление с остатком. Решение задач на деление с остатком
. Урок математики. . «Деление с остатком. Решение задач на деление с остатком». . Учитель:. Московченко Е. Н. ...Длина. Решение задач
Муниципальное общеобразовательное учреждение. средняя общеобразовательная школа №54. го Тольятти Самарской области. КОНСПЕКТ. урока ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:9 сентября 2019
Категория:Математика
Содержит:27 слайд(ов)
Поделись с друзьями:
Скачать презентацию



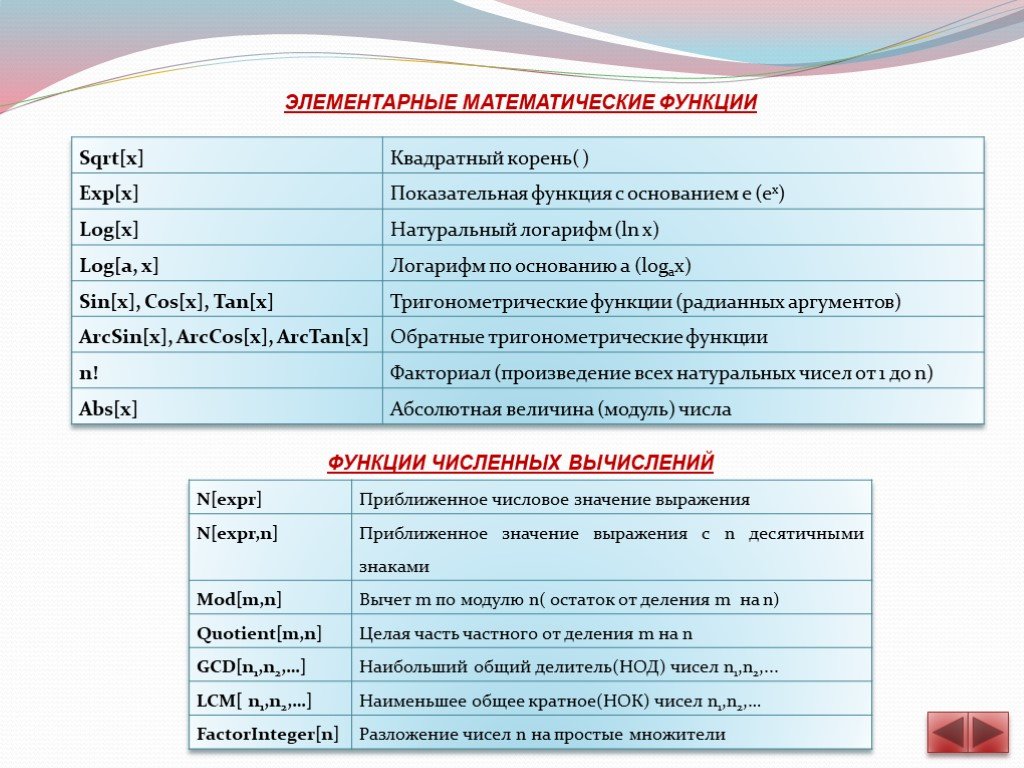



























![С помощью функции Mod вычислен остаток от деления 317 на 89. Функция Quotient вычисляет целую часть от деления 315 на 36. GCD[360,195]- найден НОД чисел 360 и 195. LCM[372,114]- найдено НОК чисел 372 и 114. С помощью функции FactorInteger число разложено на простые множители. С помощью функции Mod вычислен остаток от деления 317 на 89. Функция Quotient вычисляет целую часть от деления 315 на 36. GCD[360,195]- найден НОД чисел 360 и 195. LCM[372,114]- найдено НОК чисел 372 и 114. С помощью функции FactorInteger число разложено на простые множители.](https://prezentacii.org/upload/cloud/19/09/160691/images/thumbs/screen5.jpg)
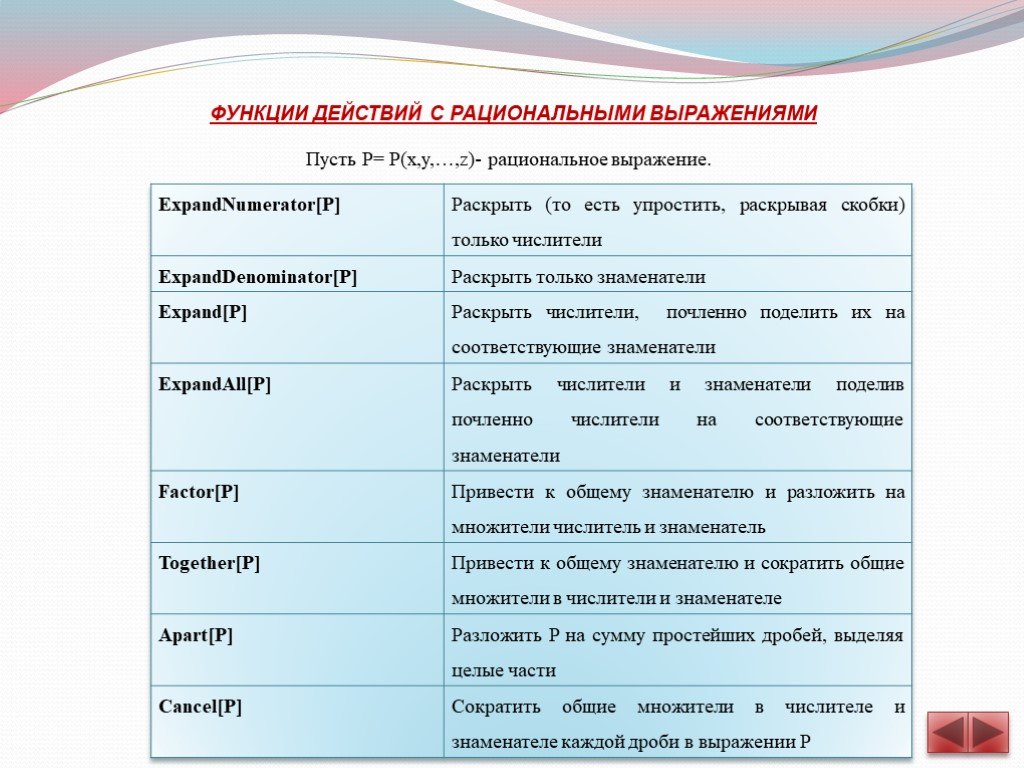
![Аргументы всех функций в программе Mathematica заключаются в квадратные скобки. Наименования встроенных функций в программе Математика начинаются с заглавных букв. Pi^4//N =97,4091- вычислено приближенное значение 25!=1۠•2•3….•24•25= 15511210043330985984000000 N[%] =0,55112*1025- это приближенное зн Аргументы всех функций в программе Mathematica заключаются в квадратные скобки. Наименования встроенных функций в программе Математика начинаются с заглавных букв. Pi^4//N =97,4091- вычислено приближенное значение 25!=1۠•2•3….•24•25= 15511210043330985984000000 N[%] =0,55112*1025- это приближенное зн](https://prezentacii.org/upload/cloud/19/09/160691/images/thumbs/screen6.jpg)



















































