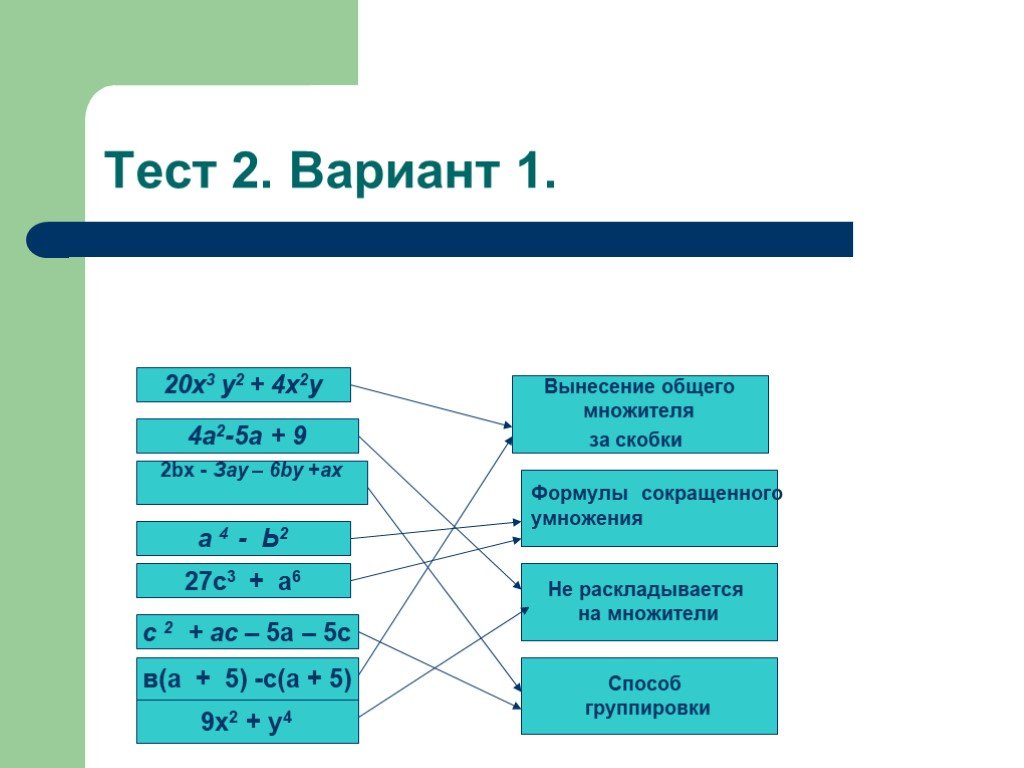
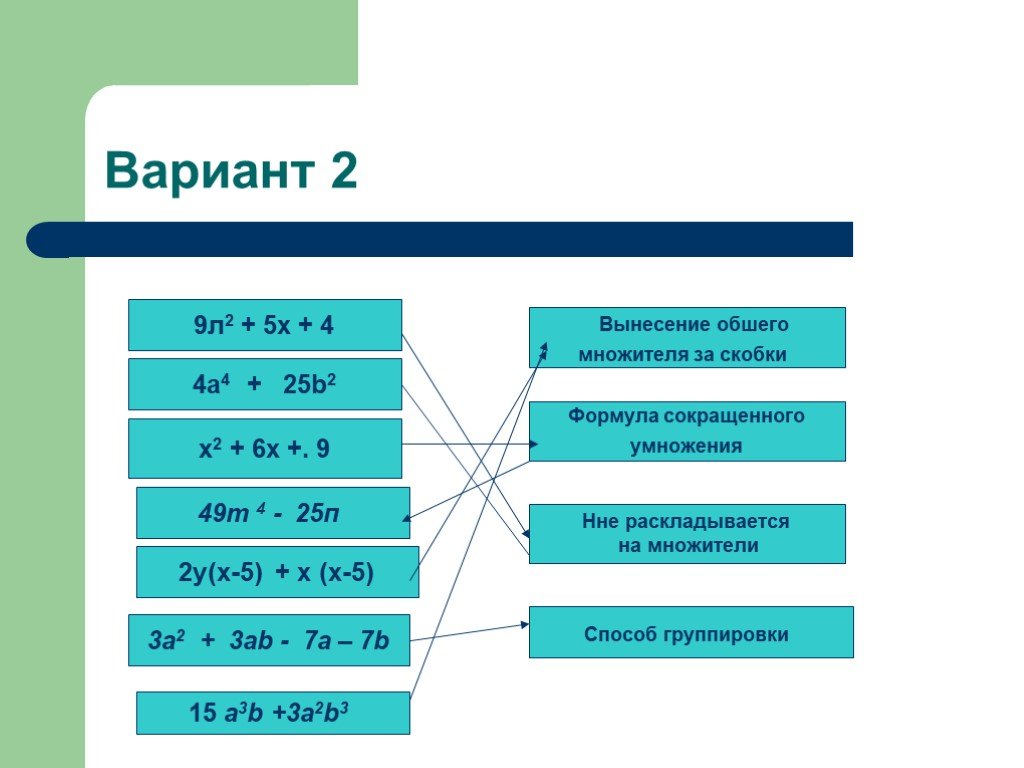
Презентация "Разложение многочлена на множители с помощью комбинации различных приемов" по математике – проект, доклад
Презентацию на тему "Разложение многочлена на множители с помощью комбинации различных приемов" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 18 слайд(ов).
Слайды презентации
Список похожих презентаций
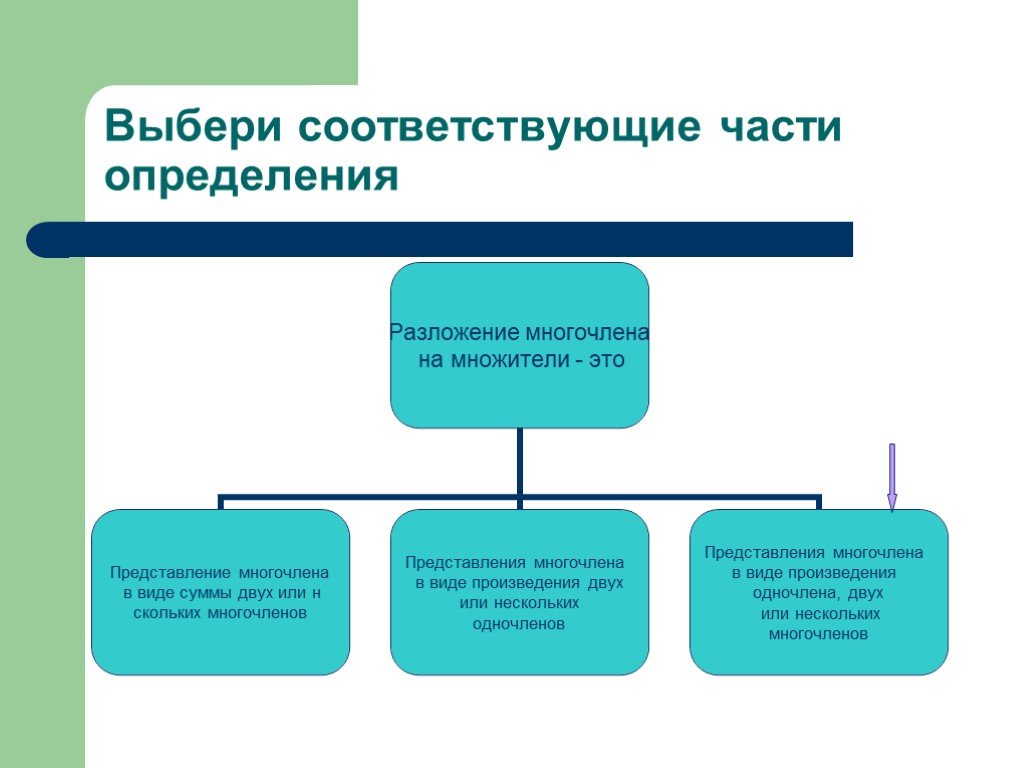
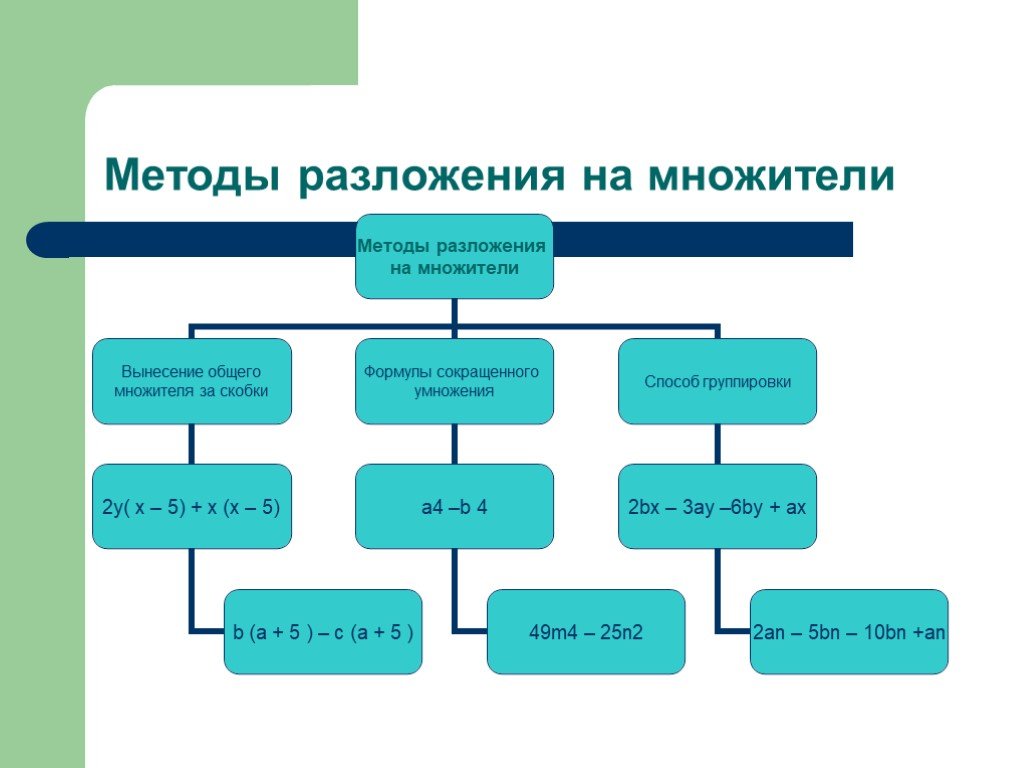
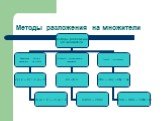
3 вида разложение многочлена на множители
1 вид вынесение общего множителя за скобки. Что значит разложить многочлен на множители? Разложить многочлен на множители — это значит представить ...Анализ контрольной работы по математике на тему "Натуральные числа и шкалы"
Натуральные числа и шкалы. 5 к л а с с № 1. Цели деятельности учителя. Главная дидактическая цель : организовать деятельность учащихся, направленную ..."Деление на десятичную дробь"
Звонок. Долгожданный дан звонок, Начинается урок Дружно за руки возьмёмся, И друг другу улыбнёмся. Пусть сегодня для нас всех, На уроке сопутствует ...Алгоритмы работы с величинами
Цель:. Познакомиться с понятием «величина» и показать ее назначение в программировании. 1. Как называется алгоритм, записанный на «понятном» компьютеру ...«Старая сказка на новый лад»
3 268 :2 12 396:3 256 130:5 1634 51226. Полетели стрелы в разные стороны. Упала стрела царевича на царский двор. 1634 м. Стрела второго царевича улетела ..."Разрезание геометрических фигур на части"
ЗАДАЧИ НА РАЗРЕЗАНИЯ. Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат. ...Активизация мыслительной деятельности на уроках математики
Активные формы урока. Урок-лекция. Урок-консультация. Урок-практикум Урок-семинар Урок-зачёт. урок-лекция. Зачёт №2 по геометрии в 11 классе 1.Объясните, ...Активные методы обучения на уроках математики и во внеурочной деятельности
Активные методы обучения — это методы, которые побуждают учащихся к активной мыслительной и практической деятельности в процессе овладения учебным ...Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD
Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение ...Аксиомы расположения точек на прямой и плоскости
Выполните действия и сделайте записи:. 1. Изобразите точку С, лежащую на прямой а. 2. Изобразите точку D, не лежащую на этой прямой. 3. Проведите ...«Действия с дробями», «Нахождение дроби и процентов от числа»
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...Алгебраические дроби с разными знаменателями
Повторить правила сложения и вычитания числовых дробей с разными знаменателями; Изучить правила сложения и вычитания алгебраических дробей с разными ...«Моя математика» - задачи на нахождение целого или части
МАТЕМАТИКА 1 3 4 5 7 6 8 9 0. Работа с числовым рядом. http://www.bajena.com/ru/kids/mathematics/sum-mathematics.php. 1. Прочитайте текст справа и ...Алгоритмы работы на координатной плоскости
Цели:. Формировать умение работать на координатной плоскости как с положительными, так и отрицательными координатами. Развивать алгоритмическое мышление. ...Алгебра логики на практике
«Всё наше достоинство заключено в мысли. Не пространство, не время, которых мы не можем заполнить, возвышает нас, она, наша мысль. Будем же учиться ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ...Алгоритм с ветвлениями и циклами.
Линейный алгоритм. "Соберись в школу" Начало Конец Встань Умойся Сделай зарядку Оденься Позавтракай Собери портфель. Ветвление. "Раскрась крышу дома". ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...«Задачи на проценты»
Тема урока: Проценты. Тип урока: урок обобщения и систематизации знаний. Цели урока: Образовательные: Обобщение и систематизация знаний учащихся о ...Конспекты
Внетабличное деление двузначногочисла на однозначное
«Внетабличное деление двузначного числа на однозначное». Цели:. Образовательная. : формировать умение выполнять внетабличное деление двузначных ...Виды углов. Умножение и деление двузначного числа на однозначное
Павлодарская область. Актогайский район. . с.Барлыбай. . . Енбекшинская средняя школа. Тема:. . «Виды углов. Умножение и деление двузначного. ...Вместе весело шагать на экзамен
КОУ ВО «ТАЛОВСКАЯ ШКОЛА-ИНТЕРНАТ ДЛЯ ДЕТЕЙ-СИРОТ И ДЕТЕЙ, ОСТАВШИХСЯ БЕЗ ПОПЕЧЕНИЯ РОДИТЕЛЕЙ». 9 КЛАСС. ПРИГОТОВИЛИ : Гриценко Р.А. Носова ...Векторы на плоскости
. Конспект. обобщающего урока по теме «Векторы на плоскости». . (геометрия 9 класс). Тема. Систематизация и обобщение изученного материала ...Больше на некоторое число
Тема:. Больше на некоторое число. Тип урока:. урок изучения нового материала и первичного закрепления. Цель:. познакомить учащихся с возможностью ...Арифметические действия с многозначными числами
Тема:. «Арифметические действия с многозначными числами». Цель:. закрепить навыки сложения, вычитания, умножения и деления многозначных чисел; ...Астрономия на координатной плоскости
Леткова Татьяна Викторовна,. учитель математики. Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа ...Алгоритм решения задачи на нахождение целого и частей
. Тимошенкова. Ирина Викторовна. Учитель начальных классов. МБ НОУ «Гимназия № 70». Г. Новокузнецк. Алгоритм. решения задачи. ...Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число
Открытый урок математики 4 класс. Тема: Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число. Цель:. формирование ...Взаимосвязанные задачи с десятичными дробями
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат. . «Мичуринский лицей». ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:13 июня 2019
Категория:Математика
Содержит:18 слайд(ов)
Поделись с друзьями:
Скачать презентацию