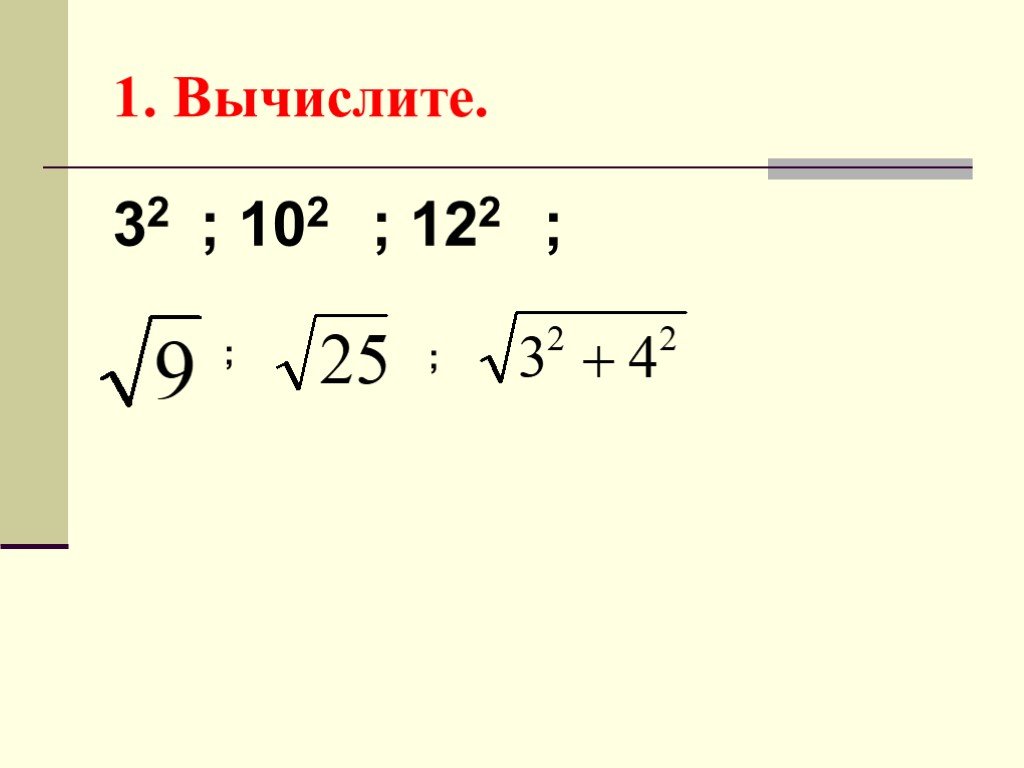Презентация "Решение систем способом подстановки" по математике – проект, доклад

Скачать презентацию (96.07 Кб) Смотреть похожие презентации Конспекты для презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Презентацию на тему "Решение систем способом подстановки" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 11 слайд(ов).

Скачать презентацию (96.07 Кб) Смотреть похожие презентации Конспекты для презентации

Слайды презентации

Слайд 1

Тема: «Решение систем, содержащих уравнение второй степени способом подстановки».

Слайд 2

1. Вычислите. 32 ; 102 ; 122 ; ;

Слайд 3

2. Назовите 3 решения уравнения: а) х – у = 1; в) 6 + 0х = 2у; б) ху = 0; г) 0х + 0у = 0.

Слайд 4

3. Выразите переменную х через у:

а) у + х = 5; г) ху = 2; б) у – х = 17; д) х – 3у =0. в) 2х – 10у = 2;

Слайд 5

4. Представьте в виде многочлена:

а) (3 + у)2 ; б) (а – 2)2

Слайд 6

5. Являются ли решением системы

х + у = 4, ху = 3; Пары чисел (2;2) ; (3;1); (6;-2).

Слайд 7

5. Решите систему уравнений:

х + у = 2, х2 + у2 = 2.

Слайд 8

Алгоритм решения системы уравнений способом подстановки.

Выразить одну переменную через другую из одного уравнения системы; Подставить полученное выражение в другое уравнение системы вместо этой переменной; Решить полученное уравнение с одной переменной; Найти значения соответствующие второй переменной.

Слайд 9

х2 + у2 = 41, х2 + у2 = 41, х2 + (1 + х)2=41, у – х = 1; у = 1 + х; у = 1 + х; х2+ 1 + 2х + х2- 41= 0, 2х2 + 2х – 40 = 0, у = 1 + х; у = 1 + х; х2 + х – 20 = 0, у = 1 + х; Решим первое уравнение системы: х2 + х – 20 = 0, Х1= Х2= Подставим эти значения во второе уравнение системы: х1= 4, х2= -5, у1 = 1 +4 = 5, у2= 1 + (-5) = -4. Ответ: (4; 5); (-5; -4).

х= 10 – 3у, х = 10 – 3у, х = 10 – 3у, ху = 3; (10 – 3у)у = 3; 10у – 3у2 - 3 = 0; Решим второе уравнение системы: -3у2 +10у – 3 = 0, 3у2 - 10у + 3 = 0, У1 = у2 = ; Подставим эти значения в первое уравнение системы: х1= 10 – 3 3=1, х2= 10 – 3 = 9, у1= 3, у2= ⅓ Ответ: (1; 3); (9; ⅓).

Слайд 10

Подберите второе уравнение так, чтобы оба уравнения составляли систему:

у = х + 2, … .

Список похожих презентаций

Графическое решение систем уравнений

Правило решения системы уравнений графическим способом. Построить графики каждого из уравнений системы. Найти координаты точки пересечения построенных ...

Итоговый урок: решение систем уравнений

ЦЕЛИ УРОКА. 1. повторить определения понятий: -система уравнений; -решение систем уравнений; -способы решения систем уравнений. 2. Найти практическое ...

Графическое решение систем уравнений

Лаборатория «ТРУД». Твори, Решай, Учись, Добивайся с интересом и удовольствием! Руководители лаборатории. Начальник лаборатории: Ноумэн Ноу Мэнович ...

Решение дробно-рациональных неравенств

Цели урока:. Повторить решение рациональных неравенств методом интервалов; Обобщить метод интервалов для решения дробно-рациональных неравенств; Закрепить ...

Решение задач на применение признаков подобия треугольников

Тема урока. Решение задач на применение признаков подобия треугольников. Цель урока: Обобщение по теме «Признаки подобия треугольников». Задачи урока:. ...

Решение задач на построение графиков алгебраических функций

Анализ содержания материала. Кто не знает в какую гавань он плывет, для того нет попутного ветра. Сенека. Главной целью данной темы является: научить ...

Решение задач на комбинации призмы, шара и пирамиды

Шар, вписанный в пирамиду. В любую треугольную пирамиду можно вписать шар; В пирамиду, у которой в основание можно вписать окружность; центр, которой ...

Решение задач на готовых чертежах. Площади фигур выполнена в powerpoint

8 9 10 11 14 15 16 17 18 30 33 34 35 1 3 4 5 6 13 19 31 7. Найти: D С В А Дано:. 2. E F. B C. Е. . P M K. К М О Р. Т. . N. 450. 12. 12 см 300 8 см. ...

Аксиомы стереометрии Решение задач

Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...

Решение задач

Восстанови ряд чисел:. 1 + 2 10 – 2 3 + 1 8 - 1 2 + 2 9 – 2 4 + 1 7 - 1 3 + 2 8 – 2 ……. ……. ……. …… ……. ……. …… …… …… ……. Угадай пример:. 10 8 9 2 2 ...

Вычитание. Решение задач с помощью действия вычитания

Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...

Блиц-опрос "Решение треугольников"

Выбери вопрос. В треугольнике АВС угол А равен 40 градусов. Внешний угол при вершине В равен 68 градусов. Найдите угол С. Угол С равен 28 градусов. ...

Бинарный урок геометрии и информатики "Четырехугольники. Решение задач" Лауреат

Проверка домашнего задания. В трапеции АВСD (АD – большее основание) диагональ АС ┴СD и делит ВАD пополам, СDА=60, периметр трапеции – 20 см. Найдите ...

Арксинус. Решение уравнения sin t = a

Цели. Изучить определение арксинуса числа. Изучить формулы решения простейшего тригонометрического уравнения sin t = a. Повторим. Что называется синусом ...

Аналитический и численный методы решения систем уравнений с параметром

АНАЛИТИЧЕСКИЙ И ЧИСЛЕННЫЙ МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ. Астрахарчик Н.А. Система симметрична относительно знака x. Система симметрична ...

Алгебра высказываний. Решение логических задач

Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...

Алггоритм. Решение задач

Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...

Решение заданий С2 ЕГЭ-2010

Задача №1:. В прямоугольной системе координат заданы точки O(0;0), D(-5;0), C(0;-12). Найдите площадь боковой поверхности конуса, полученного вращением ...

Решение задач

У Мурки 6 котят, а у Пушинки на 2 котёнка меньше. Сколько котят у Пушинки? Вере 8 лет. Она старше Риты на 2 года. Серёжа и Рита – ровесники. Сколько ...

ГИА-2012. Решение задач по теме "Чтение графиков функций"

График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...

Конспекты

Советы как сделать хороший доклад презентации или проекта

Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
Старайтесь говорить уверенно, плавно и связно.
Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.