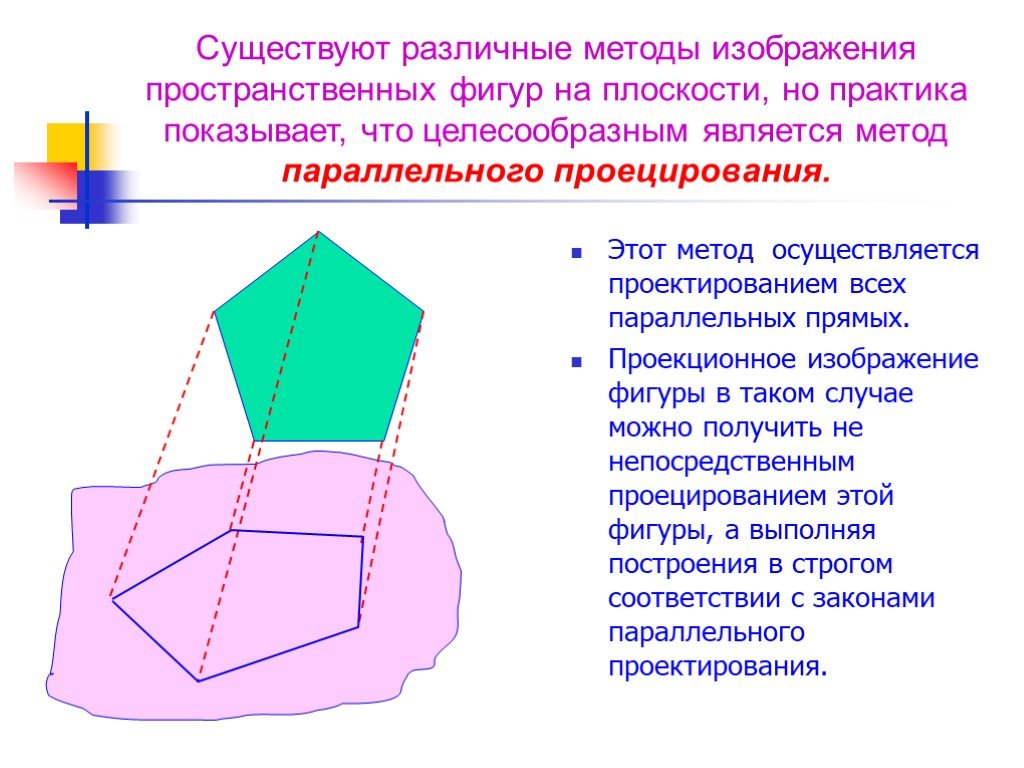
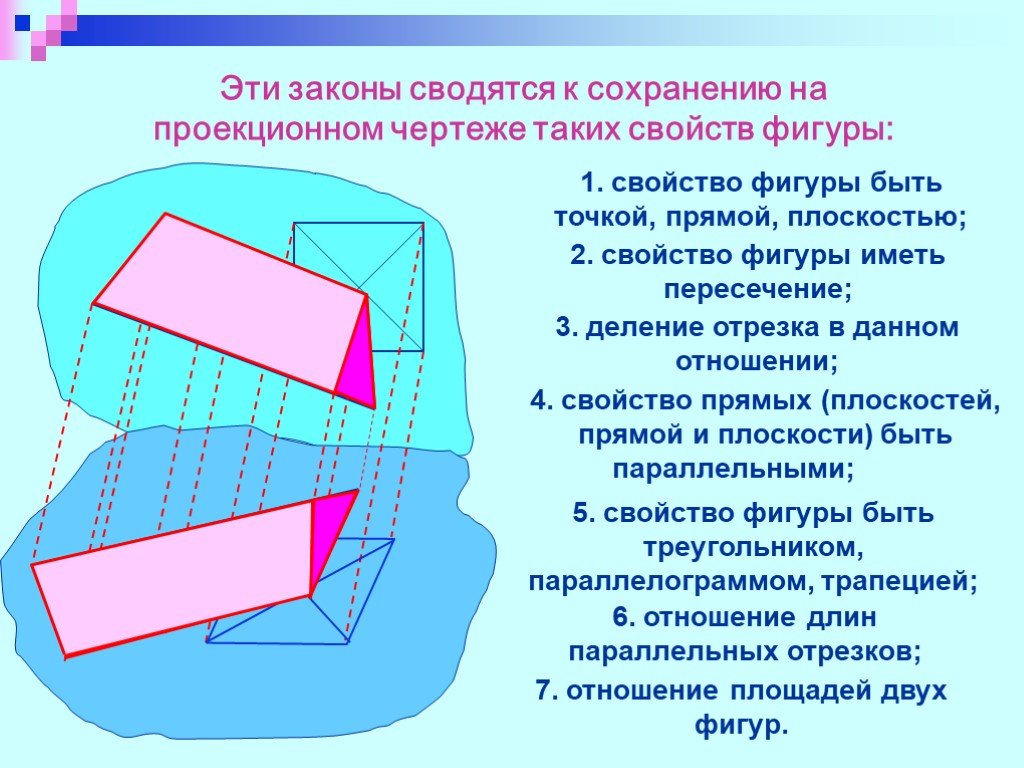
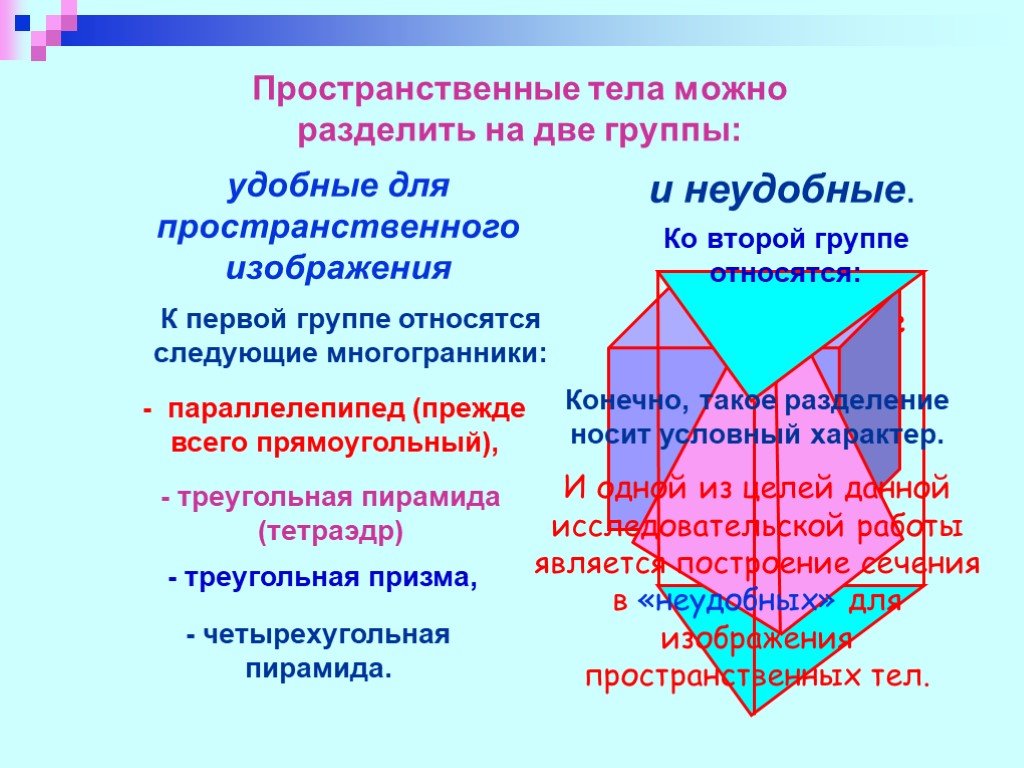
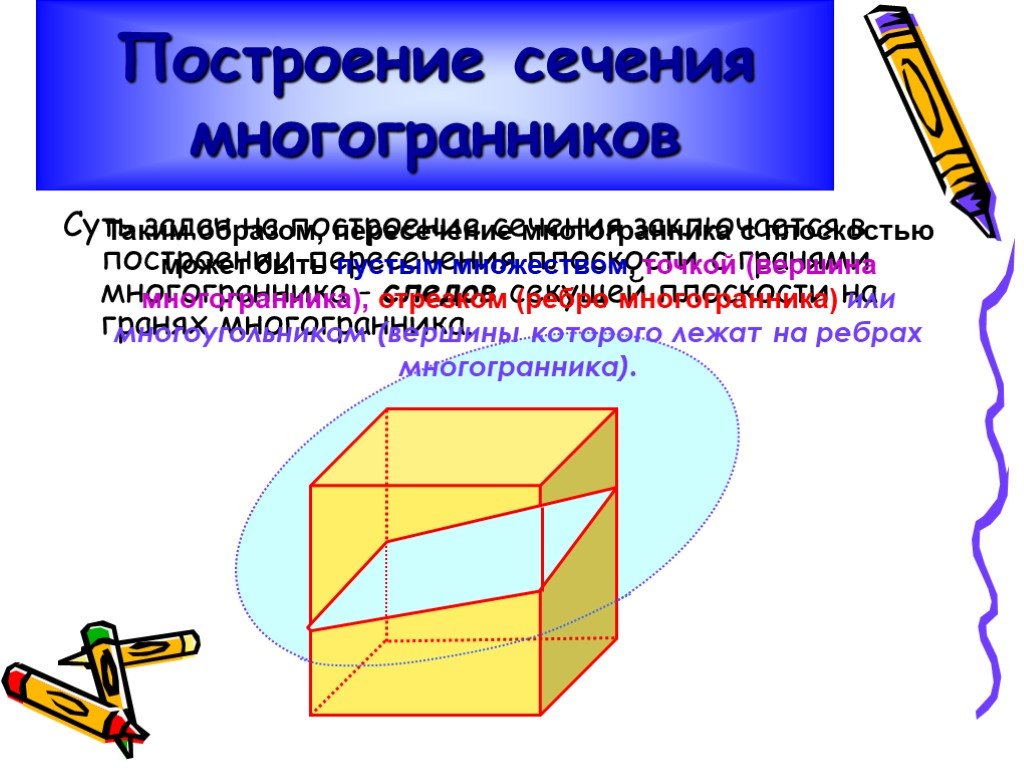
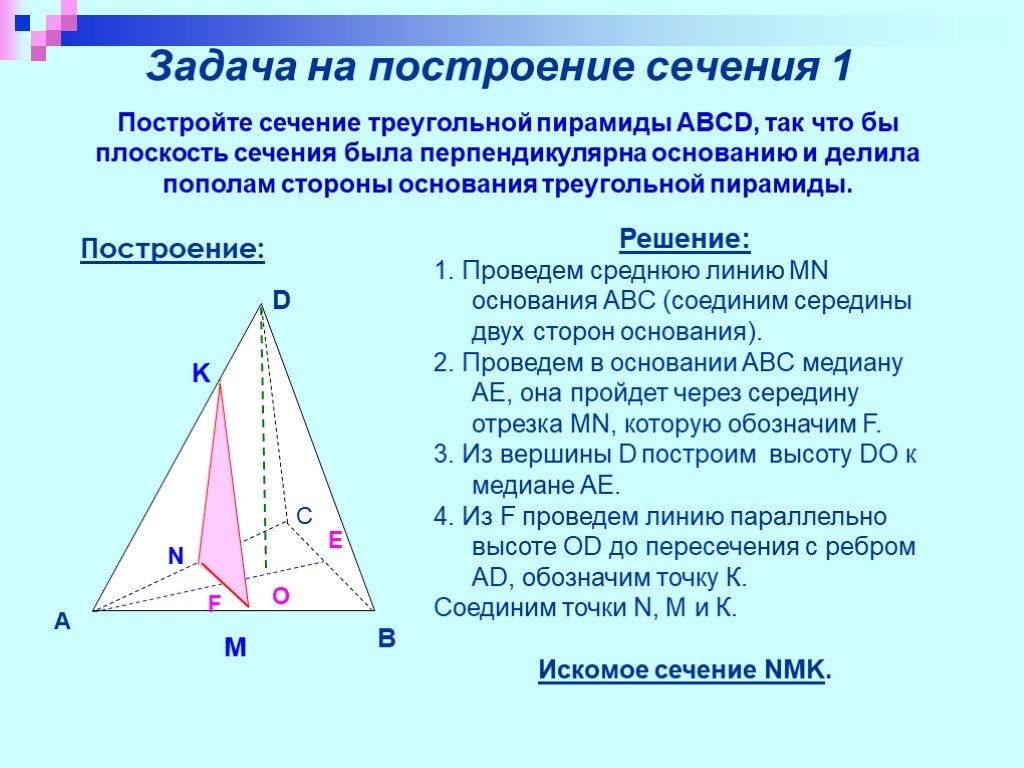
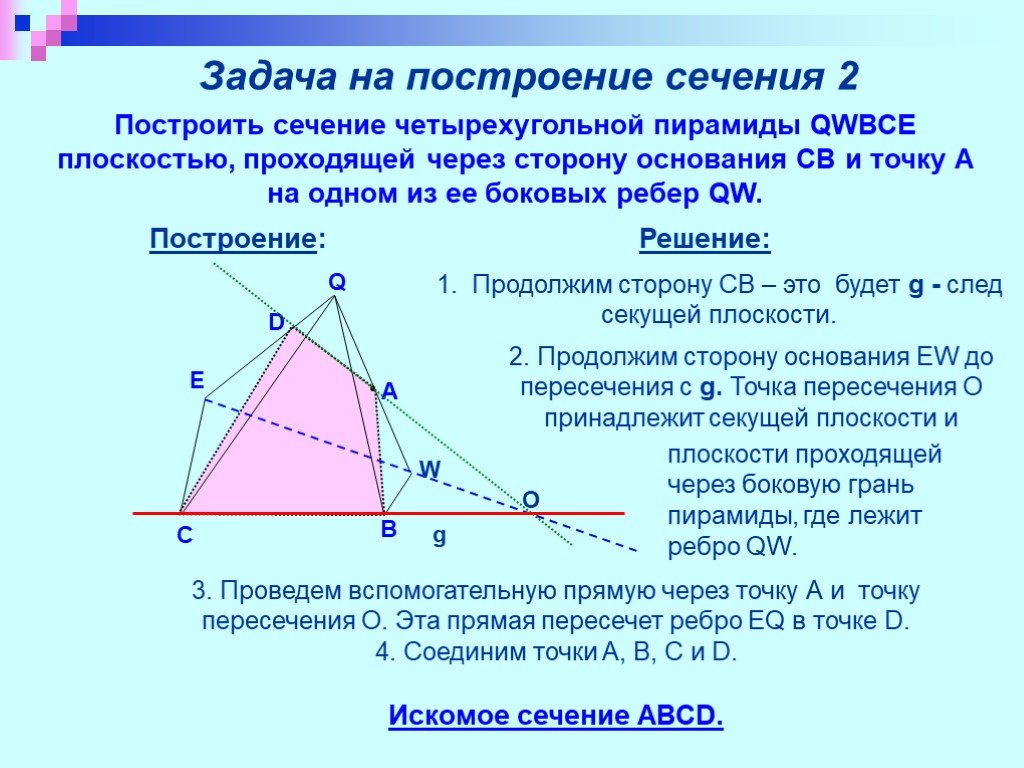
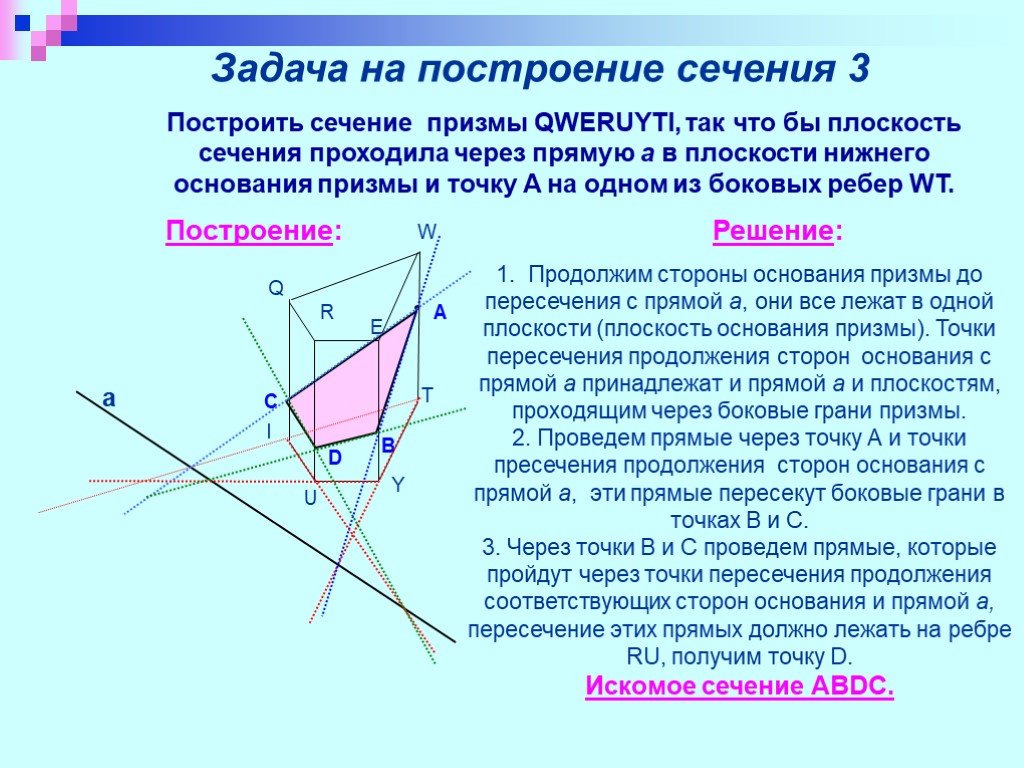
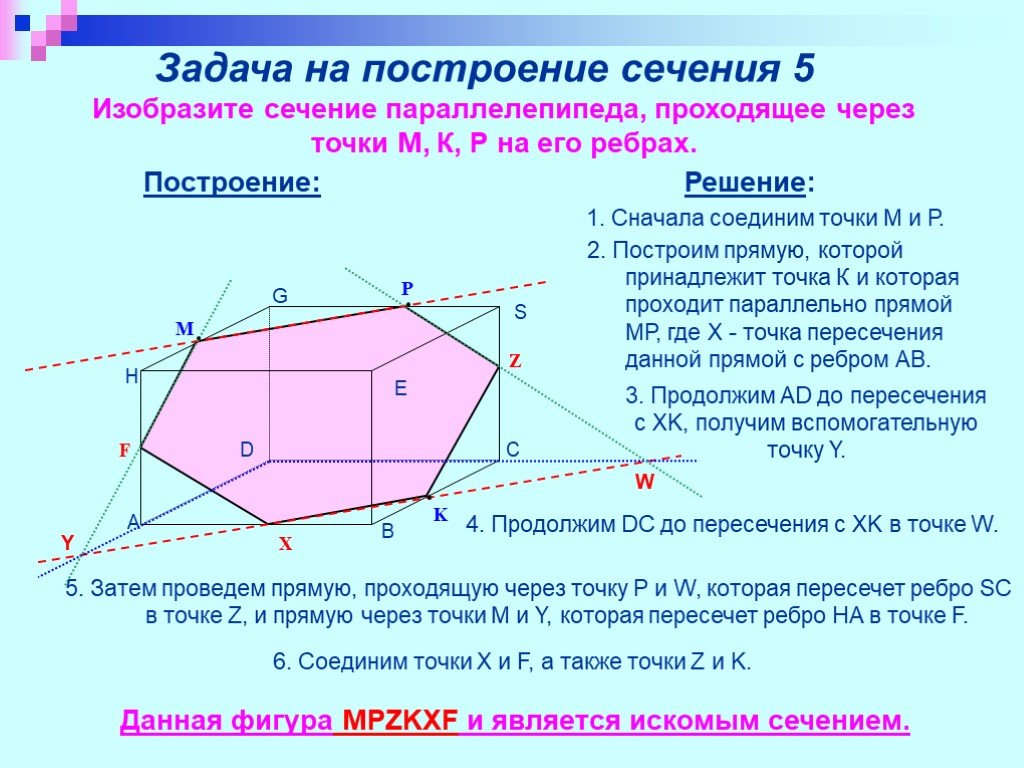
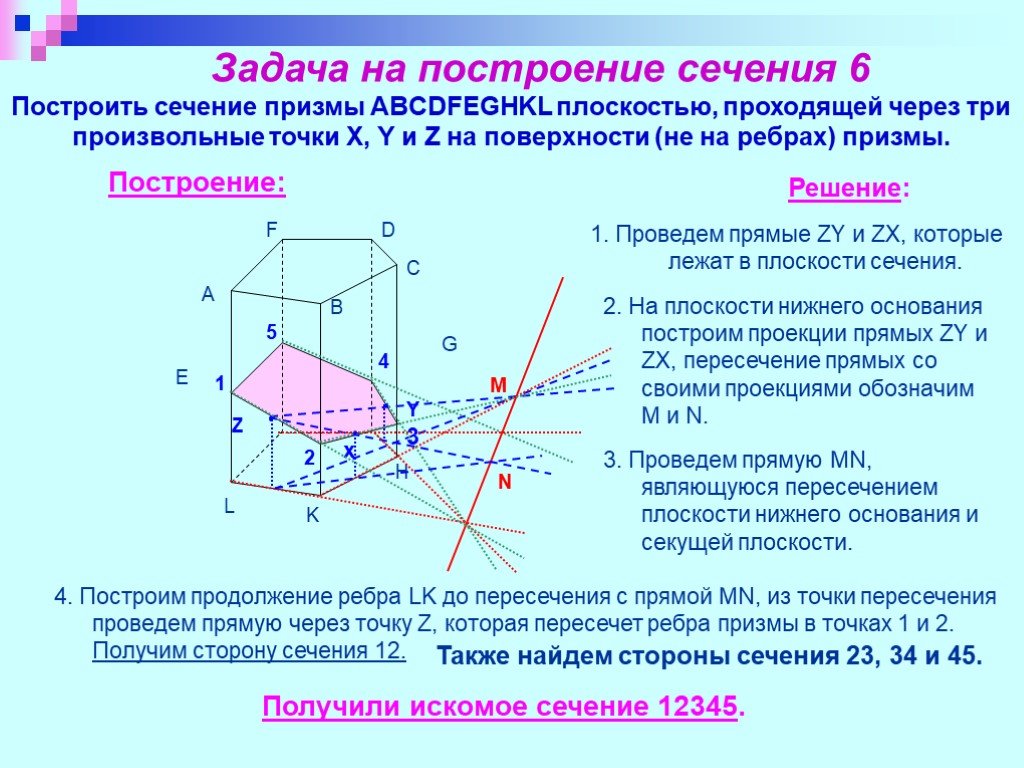
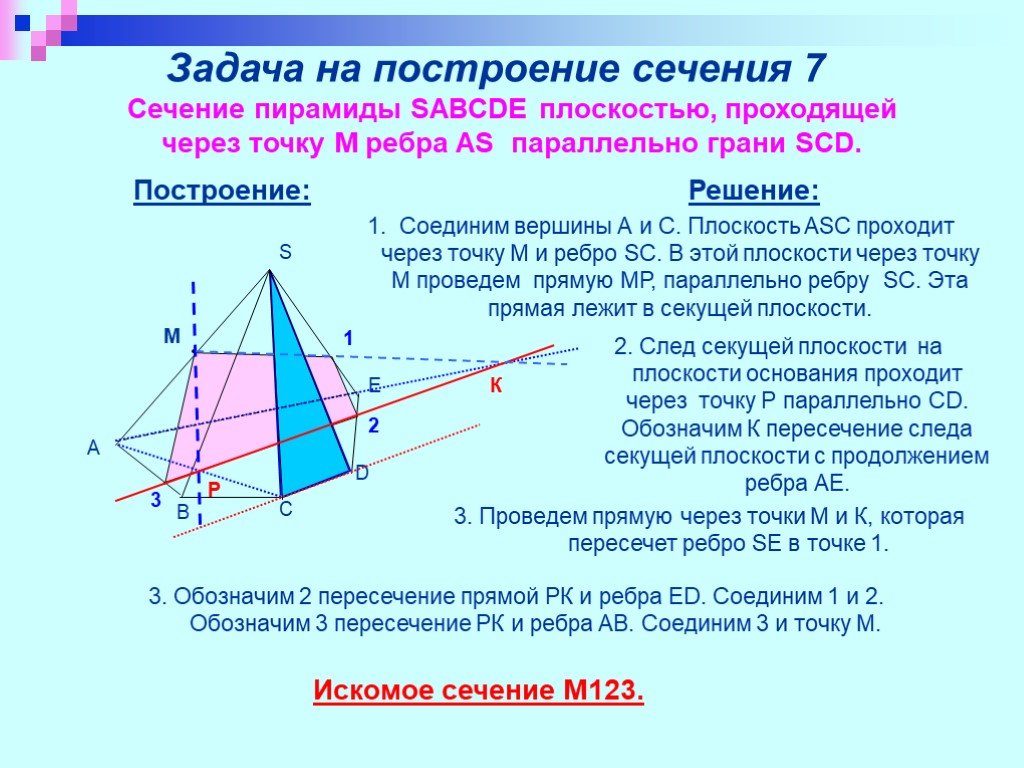
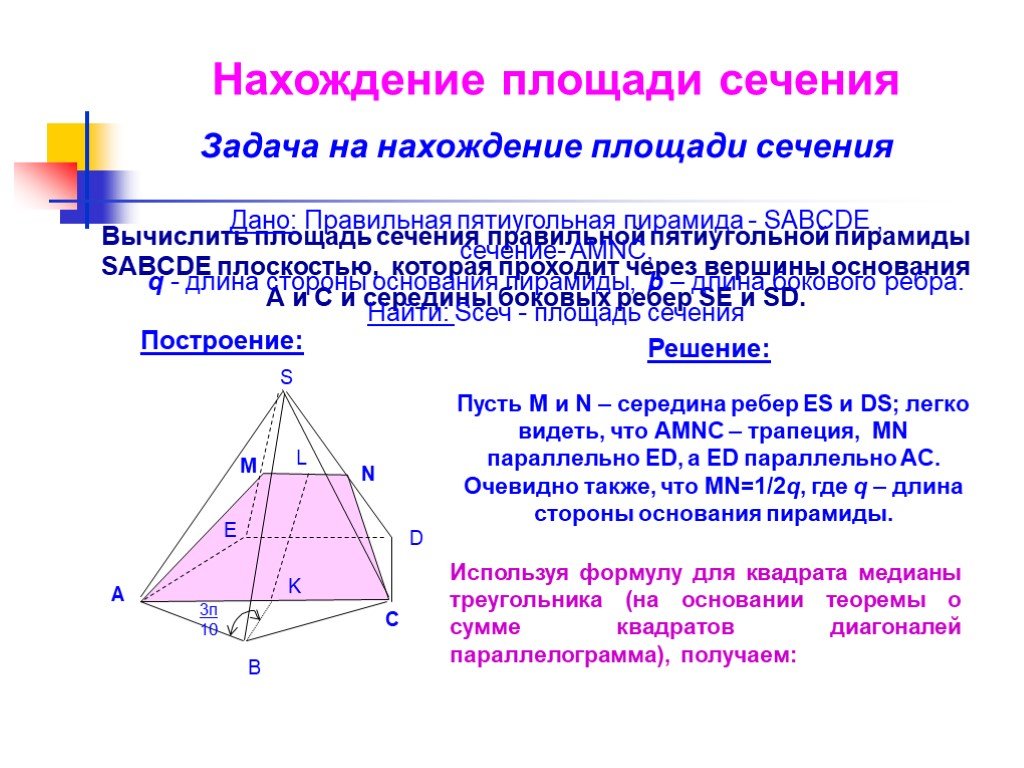
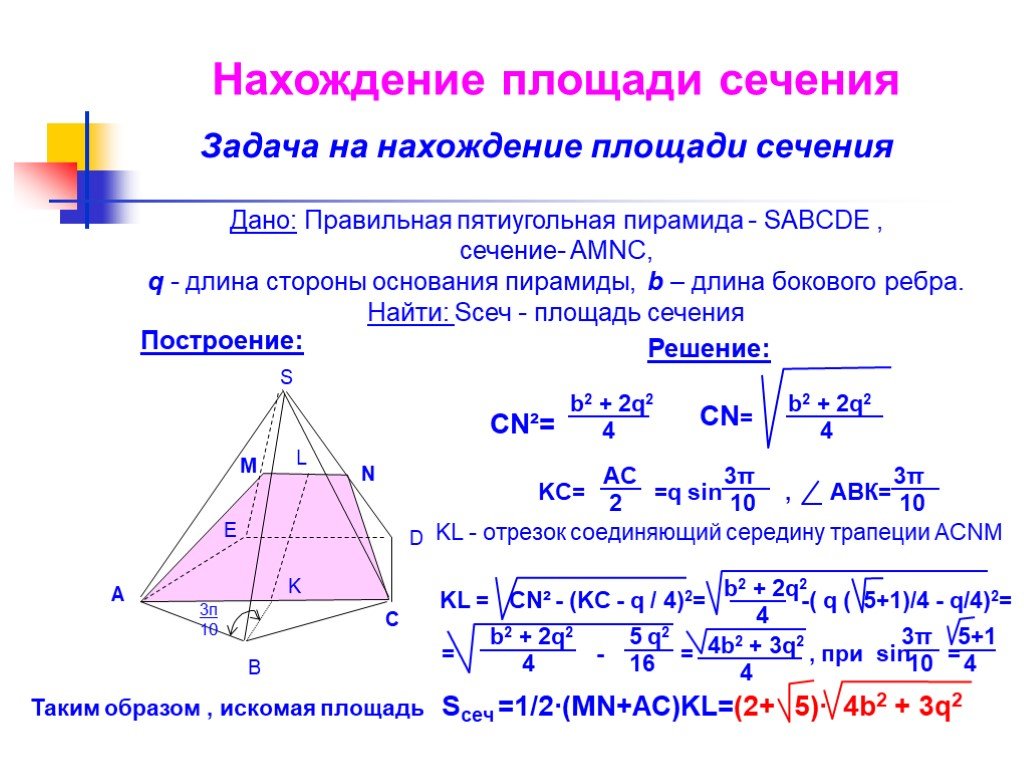
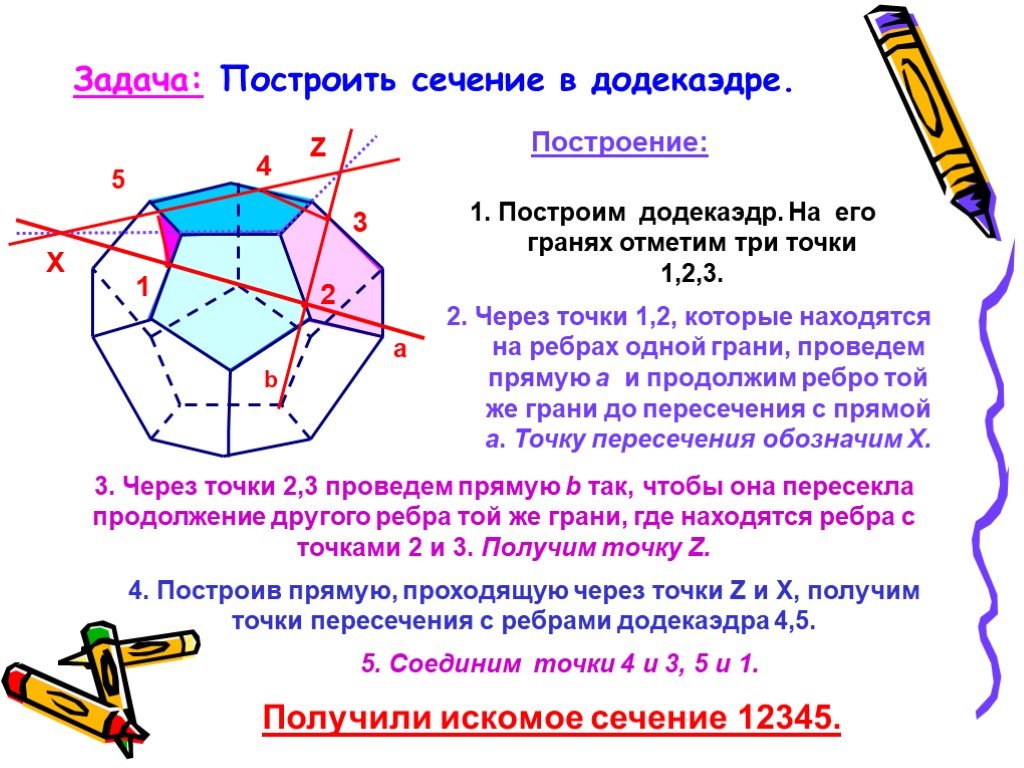
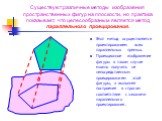
Презентация "Изучение сечений в стереометрии с помощью компьютера" по математике – проект, доклад
Презентацию на тему "Изучение сечений в стереометрии с помощью компьютера" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...Аксиомы стереометрии и их следствия
Цели:. Изучить аксиомы стереометрии: - о взаимном расположении точек, - о взаимном расположении прямых, - о взаимном расположении плоскостей в пространстве. ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...«Симметрия в пространстве» геометрия
Что такое симметрия? Симметрия в переводе с греческого означает соразмерность. Под симметрией принято понимать свойство геометрической фигуры, расположенной ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...«Математика в профессиях»
Ознакомление с типами профессий и характеристиками труда. Исследование значения математики в различных областях деятельности человека. Развитие познавательной ...Аксиомы стереометрии
1 3 4 5 А1 А3 С1. Дан куб АВСDA1B1C1D1. D1 D С В1 В А M. Точка М лежит на ребре DD1. N. Точка N лежит на ребре CC1. K. Точка K лежит на ребре BB1. ...Аксиомы стереометрии
Повторить аксиомы планиметрии Познакомиться с аксиомами стереометрии Уметь соотносить математическую формулировку аксиомы с графическим изображением ...«Действия с дробями»
Цели урока:. Устный счет. Какая часть каждой фигуры окрашена? Есть ли на чертежах ошибки? Найдите их и назовите ошибку. Нет ли в чертежах ошибок? ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ..."Симметрия в архитектуре Старого Оскола"
Остановка 1. Главная улица города – улица Ленина. Мы находимся в центре нашего города у здания администрации. Какие приемы использовал архитектор, ..."Все действия с обыкновенными дробями"
Великие открытия ученых математиков ХХ века. «Математика является значительно большим, чем наука, поскольку она является языком науки». Нильс Бор, ..."Взаимное расположение прямых в пространстве. Угол между двумя прямыми
«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Дьердье Пойа, венгерский математик. ...«Действия с дробями», «Нахождение дроби и процентов от числа»
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ...Аксиомы стереометрии
Содержание:. 1.Понятия стереометрии 2. Изображение плоскости 3.Аксиомы стереометрии 4.Следствия из аксиом стереометрии. Система аксиом стереометрии ...«Действия с обыкновенными дробями (2)»
Урок по теме «Действия с обыкновенными дробями». На острове Дробей. 1. Сократите дроби. 2. Исключите целую часть из числа. 3. Переведите число в неправильную ...Аксиомы стереометрии
ОСНОВНЫЕ ПОНЯТИЯ. Расстояние, точка, прямая, плоскость, Множество. обозначения плоскостей. М – все точки пространства. Аксиома 1. В пространстве существуют ...«Закрепление изученого» (Сложение и вычитание с переходом через десяток в пределах 20)
Цели урока:. 1. Закрепить знания о сложении и вычитании с переходом через десяток в приделах 20. 2. Упражняться в решении задач изученных видов. План ...Аксиомы стереометрии
Аксиомы стереометрии. Сформулируйте содержание аксиом А1, А2, А3, А4 Прокомментируйте их с помощью приведенных ниже рисунков. α С В А. Через любые ...Конспекты
Введение в теорию вероятностей
9 класс. Тема: Введение в теорию вероятностей.(90 мин.). Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, ...Вводное повторение. Все действия с десятичными дробями
Галкина Любовь Валентиновна. МБОУ «Новопоселёновская средняя общеобразовательная школа» Курского района Курской области. Учитель математики. ...Большие и малые числа в химии
МКОУ «Средняя общеобразовательная школва №5. . города Ершова Саратовской области». . Бинарный урок. Большие и малые числа в химии. Провели ...Бородинское сражение в математических задачах
Открытый урок «Бородинское сражение в математических задачах». Карташова Ирина Викторовна , учитель математики МБОУ «Бирюковская СОШ». Техническое ...Арифметические действия с числами
Методическая разработка урокаматематики. «Арифметические действия с. числами. ». для учащихся 6-го класса. Аннотация. Повторение изученного ...Арифметический способ отбора корней в тригонометрических уравнениях
Конспект урока для 11 класса на тему «Арифметический способ отбора корней в тригонометрических уравнениях». Цели и задачи урока:. . . повторение ...Арифметические действия с положительными и отрицательными числами
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Методическая разработка урокаматематики. «Арифметические действия ...Арифметические действия с целыми числами
Ваш выбор: «Курить или долго жить.». Урок по математике в 6 кл коррекционной школы. Тип урока. . Обобщение и закрепление знаний по теме : ...Арифметические действия с дробями
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Методическая разработка урокаматематики. «Арифметические действия ...Арифметические действия с многозначными числами
Тема:. «Арифметические действия с многозначными числами». Цель:. закрепить навыки сложения, вычитания, умножения и деления многозначных чисел; ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:12 марта 2019
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию