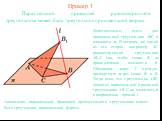
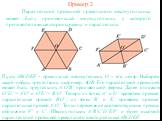
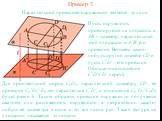
Презентация "Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы" по математике – проект, доклад

Теорема

Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования π, то ее проекция F’ на эту плоскость будет равна фигуре F.

Пример 1

Параллельной проекцией равностороннего треугольника может быть треугольник произвольной формы.

Действительно, пусть дан произвольный треугольник ABC в плоскости π. Построим на одной из его сторон. например, AC равносторонний треугольник AB1C так, чтобы точка B1 не принадлежала плоскости π. Обозначим через l прямую, проходящую через точки B1 и B. Тогда ясно, что треугольник ABC является параллельной проекцией треугольника AB1C на плоскость π в направлении прямой l.

Аналогично, параллельной проекцией прямоугольного треугольника может быть треугольник произвольной формы.

Пример 2

Параллельной проекцией правильного шестиугольника может быть произвольный шестиугольник, у которого противоположные стороны равны и параллельны.

Пусть ABCDEF – правильный шестиугольник, O – его центр. Выберем какой-нибудь треугольник, например, AOB. Его параллельной проекцией может быть треугольник A’O’B’ произвольной формы. Далее отложим O’D’ = A’O’ и O’E’ = B’O’. Теперь из точек A’ и D’ проведем прямые, параллельные прямой B’O’; из точек B’ и E’ проведем прямые, параллельные прямой A’O’. Точки пересечения соответствующих прямых обозначим F’ и C’. Шестиугольник A’B’C’D’E’F’ и будет искомой параллельной проекцией правильного шестиугольника ABCDEF.

Пример 3

Параллельной проекцией окружности является эллипс.

Для произвольной хорды C1D1, параллельной диаметру CD, ее проекция C1’D1' будет параллельна C’D', и отношение C1’D1':C1D1 будет равно k. Таким образом, проекция окружности получается сжатием или растяжением окружности в направлении какого-нибудь ее диаметра в одно и то же число раз. Такая фигура на плоскости называется эллипсом.

Пусть окружность проектируется на плоскость π. AB – диаметр, параллельный этой плоскости и A’B' его проекция. Возьмем какой-нибудь другой диаметр CD и пусть C’D' - его проекция. Обозначим отношение C’D':CD через k.

Упражнение 1

Какие фигуры могут служить параллельными проекциями треугольника?

Ответ: Треугольник или отрезок.

Упражнение 2

Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник?

Ответ: а), б), в) Да.

Упражнение 3

Какой фигурой может быть параллельная проекция прямоугольника?

Ответ: Параллелограммом или отрезком.

Упражнение 4

Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция?

Ответ: а), б), в) Да; г) нет.

Упражнение 5

Верно ли, что проекцией ромба, если он не проектируется в отрезок, будет ромб?

Ответ: Нет.

Упражнение 6

Параллельной проекцией каких фигур может быть квадрат?

Ответ: Параллелограммов.

Упражнение 7

В какую фигуру может проектироваться трапеция?

Ответ: Трапецию или отрезок.

Упражнение 8

Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы?

Ответ: а) Да; б), в) нет.

Упражнение 9

Треугольник A’B’C’ является параллельной проекцией треугольника ABC. Расстояния между соответствующими вершинами этих треугольников равны a, b, c. Найдите расстояние между точками пересечения медиан треугольников.

Ответ: