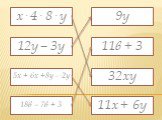
Презентация "Упрощение выражений" (5 класс) по математике – проект, доклад
Презентацию на тему "Упрощение выражений" (5 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 15 слайд(ов).
Слайды презентации
Список похожих презентаций
Упрощение выражений
Цели:. Совершенствовать умение учащихся выполнять упрощение выражений Продолжить работу над задачами, решаемыми способом составления уравнения. План ...Упрощение выражений.
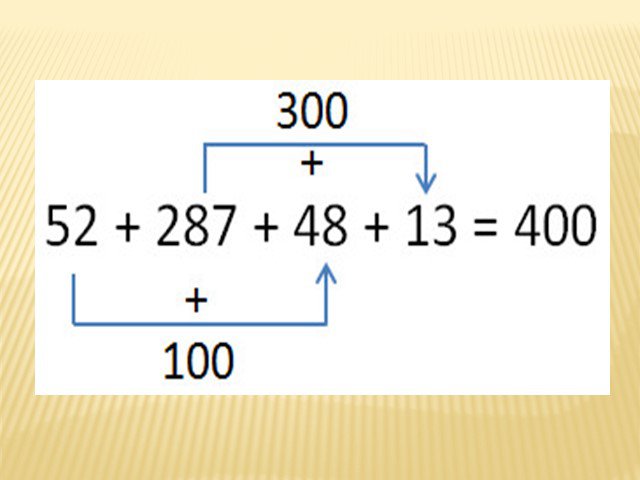
Вычислите. 90 45 3 84 9 - 45 : 15 :8 36 18 5. Найдите значения выражений удобным способом. 125 · 67 · 8 45 · 8 + 25 ·8 25 · 19 · 4 81 · 74 + 19 · ...Упрощение выражений, задачи на части, порядок действий
1.Вычисли 1) 57: 19 = 3 2) 90 : 45 3) 27 * 11 5)2025 : 5 4) 560 : 70 = 297 = 8 = 405 6) 125 * 8 = 1000 7)693 : 3 = 231. 2. Найди значение выражения. ...Упрощение выражений
Восстановите цепочку вычислений. 30 90 45 3 51 100 50 76 84 19 ∙ 3 - 45 : 15 ∙ 17 + 49 ∙ 4 : 3 + 8. Решите задачу:. На 5 грузовиках 75 ящиков. Сколько ...Упрощение выражений
Цель:. Создать тест для использования на уроках математики. Задачи:. Выяснить, как можно использовать игры и тесты на уроках Уточнить виды игр, тестов ...Упрощение выражений
Дружок! Ты уже пятиклассник.Ты много знаешь и многое умеешь. Но каждый урок учит тебя чему-то новому. Сегодня мы продолжим учиться упрощать выражения, ...Упрощение выражений
Существовало огромное количество динозавров разного облика и размера. Среди них встречались не только самые крупные животные, когда-либо ходившие ...Упрощение выражений
Восстановите цепочку вычислений. – 69 : + 60 8 96 47 19 30 57 max 10. –59 100 +49 :15 –45 +17 90. Восстановите цепочки вычислений. 20.05.2019. Бакреу ...Упрощение выражений
Вычислите. 90 45 3 84 9 - 45 : 15 :8 36 18 5. Сегодня мы вспомним, как приводили подобные слагаемые в 5 классе.А я помню, мы использовали распределительное ...
Упрощение выражений
Цель урока: научить детей упрощать выражения; выработать умение по упрощению выражений. Устный опрос. Какие законы арифметических действий вы знаете? ...Упрощение выражений
Цели урока. ознакомить учащихся с распределительным свойством умножения относительно сложения и вычитания; учить применять свойство при устных и письменных ...Упрощение выражений
Упрощение выражений. 5 класс. a + b = b + a (a + b) + c = a + (b + c). Каратанова Марина Николаевна, МОУ СОШ №256, г.Фокино. a : b = c a : a = 1 0 ...Упрощение выражений
Вычислите наиболее удобным способом:. 125 • 25 • 77 • 4 • 8 = 25 • 399 = 42 • 23 + 17 • 18 + 24 •17 =. Значение выражения 48•75 – 70•45 легко вычислить, ...Упрощение выражений"
МАРШРУТНЫЙ ЛИСТ. ВОКЗАЛ. Мы начинаем наше путешествие. А что нужно для того, чтобы оно было приятным и безопасным? Конечно же, профессиональная бригада ...Законы булевой алгебры и упрощение логических выражений
Что изучает логика? Какие формы мышления существуют? Что такое сложное высказывание? Сколько Вы знаете базовых логических операций? Перечислите названия ...Преобразование алгебраических выражений
Девиз урока:. Математику нельзя изучать, наблюдая как это делает сосед. План урока:. Сообщение темы урока. Рефлексия на начало урока Этап проверки ...Правила преобразования логических выражений
ЗАКОНЫ ЛОГИКИ. ПРАВИЛА ПРЕОБРАЗОВАНИЯ. Правило коммутативности А & В = В & А А v В = В v А Правило ассоциативности (А & В) & C = A & (В & C) (А v ...Преобразование выражений содержащих квадратные корни
Свойства арифметического квадратного корня. Квадратный корень из произведения и дроби. Квадратный корень из степени. При любом. Теорема 1 . ...Преобразование выражений
Какие свойства действий позволяют без выполнения вычислений утверждать, что верно равенство:. Найдите значение выражения и укажите, какие свойства ...Умножение разности двух выражений на их сумму
1. 72=14 2. (-3a)2=-9a2 3. (-2b)2=4b2 4. (-4)2=16 5. (3а3)2=3а6 6. -7ху-3ху= -10ху 7. -6а+10а=16а. Верны ли утверждения :. а) (х-2)(х+2) б) (х-6)(х+6) ...Конспекты
Упрощение выражений
ФИО автора материала:Хабибуллина Лейсан Ришатовна. Место работы: МБОУ СОШ №3 с.Толбазы муниципального района Аургазинский район Республики Башкортостан. ...Упрощение выражений
Козловская муниципальная образовательная школа. . Методическая разработка урока математики «Упрощение выражений». . для учащихся 5 класса. ...Упрощение выражений
Конспект урока для 5 класса по теме «Упрощение выражений». . . . Оборудование. :. . Корзиночки (изготовленные из картона);. ...Упрощение выражений
Демишева Л.В. школа №13. Тема урока:. . Упрощение выражений. Цели урока. : продолжить работу по формированию умения применять распределительное ...Упрощение выражений
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа. города Химки Московской области. ...Упрощение выражений
Конспект урока математики в 5 классе. . Тема урока. : «Упрощение выражений». Тип урока. : урок обобщения и систематизации знаний, закрепления ...Упрощение выражений
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ. средняя общеобразовательная школа №1. имени Героя Российской Федерации Ю.Д.Недвиги. . муниципального ...Упрощение выражений
Урок №. Тема: «Упрощение выражений». Цели урока:. . • Образовательная: повторение правил действий с положительными и отрицательными числами, ...Упрощение выражений
Урок математики в 5 классе «Упрощение выражений». Цели: формирование знаний распределительного закона умножения; умений упрощать выражения, зная ...Упрощение выражений
Технологическая карта учителя математики: Ларцевой Т.И. Предмет. : математика. Класс. : 5. Автор УМК. : И.И. Зубарева, А.Г. Мордкович. Тема урока. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Математика
Классы:
Содержит:15 слайд(ов)
Поделись с друзьями:
Скачать презентацию