Презентация "Расстояние между точками" по математике – проект, доклад
Презентацию на тему "Расстояние между точками" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 16 слайд(ов).
Слайды презентации
Список похожих презентаций
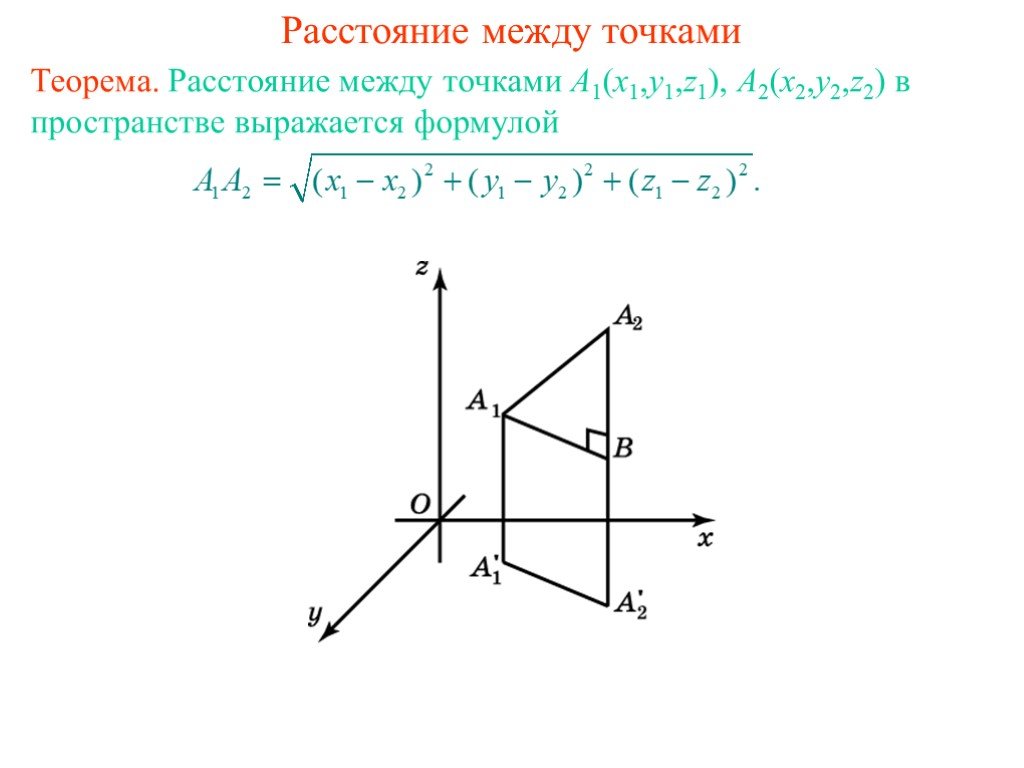
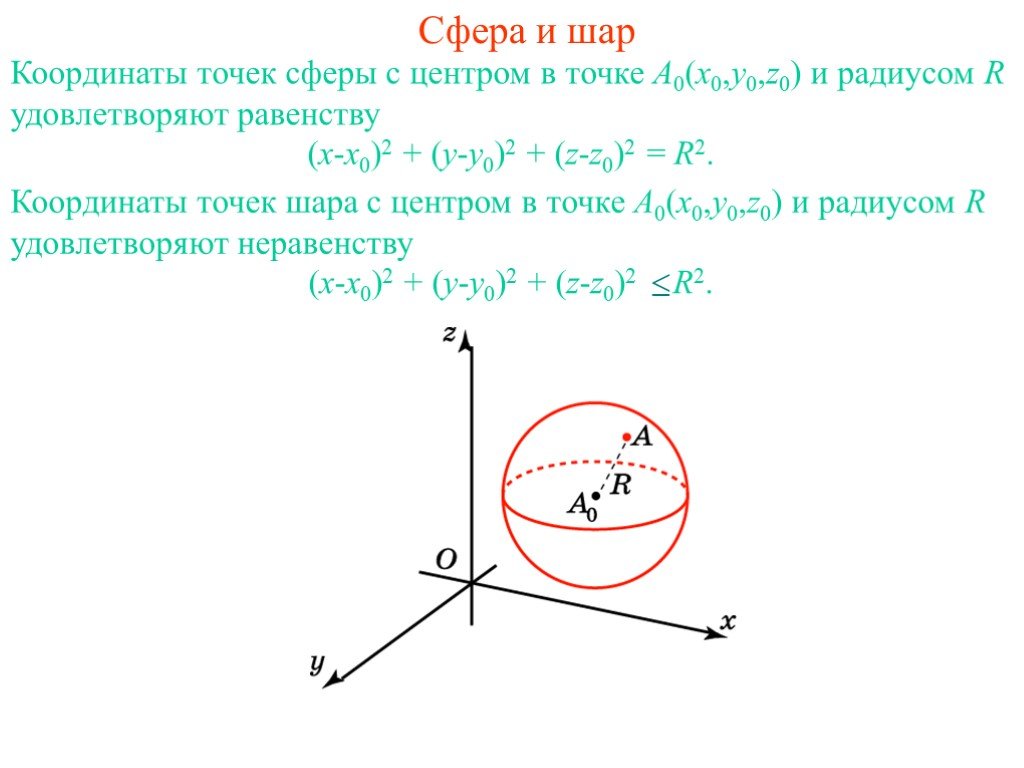
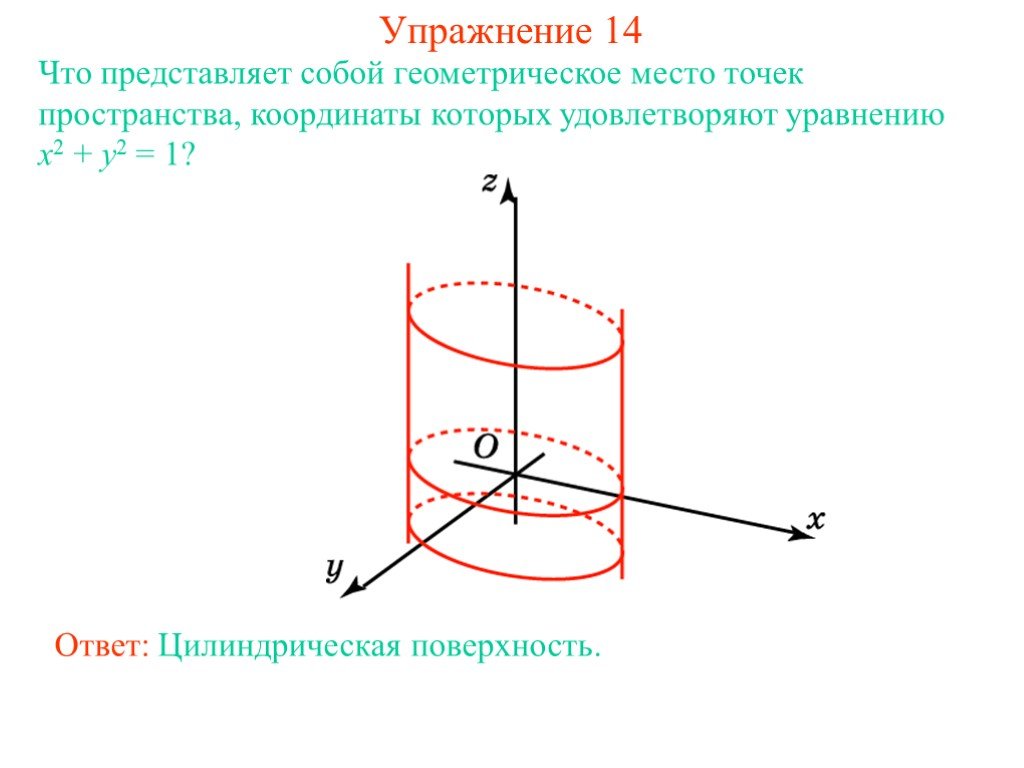
Расстояние между точками
Самостоятельная работа. А(1; 0) С(3; 2) D(2; -1) В(2; 3) О(а; в). А(3; -1); В(-2; 4); С(1; 0); D(0; -2). Найти координаты середины отрезка АВ, АС, ...Расстояние между скрещивающимися прямыми
Основные понятия. Расстоянием между скрещивающимися прямыми называется длина общего перпендикуляра к данным прямым Расстоянием между скрещивающимися ...Скорость, расстояние, время и таинственные отношения между ними
Ход урока:. Устные упражнения. Работа по теме урока. Итог урока. Домашнее задание. S – расстояние t – время v - скорость. S = v * t v = S : t t = ...Расстояние между скрещивающимися прямыми
Материал, полученный и собранный в ходе работы над проектом, является незаменимым при подготовке к решению задач ЕГЭ С2. Умение решать задачи на нахождение ...Как измерить расстояние между родственниками
Графом называют множество, в котором некоторые пары элементов выделены; элементы каждой выделенной пары называют смежными друг другу или просто смежными. ...Взаимосвязь между скоростью, временем, расстоянием
Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении ...Зависимость расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до этой прямой
Цель:. Определение зависимости расстояния между точками пересечения прямой и окружности и расстояния от центра окружности до прямой. Задачи:. Рассмотреть ...Угол между прямыми
Цели урока:. Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами. Научиться находить угол между прямыми в пространстве. ...Угол между прямой и плоскостью
Перпендикулярны ли прямые а и в? Ответ обоснуйте. А В С D F b a. ABCD- прямоугольник, FB┴(ABC). ABCD- параллелограмм, FB┴(ABC). C B O ABCD- ромб, ...Двугранный угол. Угол между плоскостями
Основные понятия. Прямая а разделяет плоскость на две полуплоскости. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями ...Соотношения между сторонами и углами треугольника
Теорема о площади треугольников. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Стороны треугольника пропорцианальны ...Зависимость между синусом, косинусом и тангенсом одного и того же угла
∙. . . П р о в е р ь и о ц е н и с е б я ! Ордината Абсцисса. О с н о в н о е т р и г о н о м е т р и ч е с к о е т о ж д е с т в о :. a2-b2=(a-b) ...Связь между суммой и слагаемыми
Цель урока. Познакомить со взаимосвязью сложения и вычитания Вывести правило нахождения неизвестного слагаемого Формировать вычислительные навыки. ...Перпендикуляр и наклонная. Угол между прямой и плоскостью.
Перпендикуляр и наклонная. 1.Перпендикуляр МН – отрезок прямой, перпендикулярной к прямой a, проходящей через точку М. MН – перпендикуляр к прямой ...Перпендикуляр и наклонная. Расстояние в пространстве
Математический диктант. Сравните катет и гипотенузу прямоугольного треугольника. Что больше и почему? Сформулируйте теорему Пифагора. Назовите гипотенузу ...Отношения между множествами
Введение. Предметом обсуждения этого урока является сам термин «множество», «элемент множества» и «отношения между множествами». Вначале мы должны ...Модель отношения между понятиями
Модель отношения между понятиями. Описание природного явления или любого другого объекта в виде текста – это текстовая модель. Изображение объекта ...Угол между прямыми в пространстве
В кубе A…D1 найдите угол между прямыми: A1C1 и B1D1. Ответ: 90o. В кубе A…D1 найдите угол между прямыми: AA1 и BC. В кубе A…D1 найдите угол между ...Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку ...Установление соотношения между сторонами и углами прямоугольного треугольника
? Это - ? (какой треугольник). Актуализация. Практическая работа «Установление соотношения между сторонами и углами прямоугольного треугольника» Цель: ...Конспекты
Взаимосвязь между скоростью, временем и расстоянием
Урок математики в 4 классе. Тема. Взаимосвязь между скоростью, временем и расстоянием. Вид урока:. закрепление полученных знаний. . . . ...Взаимосвязь между скоростью, временем и расстоянием
Конспект урока по теме: «Взаимосвязь между скоростью, временем и расстоянием». Цель деятельности учителя:. способствовать развитию умений составлять ...Связь между величинами: скорость, время, расстояние
Тема: "Связь между величинами: скорость, время, расстояние". . . Цели: продолжить работу по формированию решения задач на движение; отрабатывать ...Взаимосвязи между скоростью, временем и расстоянием
Муниципальное бюджетное общеобразовательное учреждение. «Пришибинская основная общеобразовательная школа». . Конспект урока по математике ...Сопоставление согласных звуков по твёрдости – мягкости. Составление и решение задач. Измерение расстояния между точками одного цвета
МБОУ «Средняя общеобразовательная школа №26. с углубленным изучением отдельных предметов». . Нижнекамского муниципального района Республики Татарстан. ...Угол и расстояние между скрещивающимися прямыми
Урок геометрии. . "Угол и расстояние между скрещивающимися прямыми". . . Учитель: Федорова Е.В., МОУ «СОШ № 77», г.Саратов. . Учебный план ...Соотношения между сторонами и углами прямоугольного треугольника
Конспект урока на тему «Соотношения между сторонами и углами прямоугольного треугольника». 1. Оргмомент. Слайд 1. Здравствуйте. Поднимите ...Соотношения между сторонами и углами прямоугольного треугольника
Оноприенко Л.Н.;. . учитель математики ШЛ №27. . (из опыта работы). Урок по теме. : Соотношения между сторонами и углами прямоугольного треугольника. ...Соотношения между единицами измерения массы
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 18». г. Абакан Республика Хакасия. Конспект урока ...Единицы измерения времени — час и минута, соотношения между ними
Урок математики во 2 а классе. учителя СОШ №46 г. Караганды. Кузнецовой Г.В. Тема:. Единицы измерения времени — час и минута, соотношения между ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:6 декабря 2018
Категория:Математика
Содержит:16 слайд(ов)
Поделись с друзьями:
Скачать презентацию