Конспект урока «Угол и расстояние между скрещивающимися прямыми» по геометрии для 10 класса
Урок геометрии
"Угол и расстояние между скрещивающимися прямыми"
Учитель: Федорова Е.В., МОУ «СОШ № 77», г.Саратов
Учебный план - 5ч. в неделю (из них 2 ч - геометрия)
Учебник «Геометрия, 10-11» Л.С.Атанасян
Источники информации.
1. Б.Г.Зив. Задачи к урокам геометрии.7-11 классы.
2. «Геометрия, 10-11» И.Ф.Шарыгин.
3. Сборники задач для абитуриентов.
4. Интернет ресурсы.
Тип урока: урок повторения, обобщения и систематизации знаний.
Цели урока:
Образовательные:
-
обобщить и систематизировать знания и способы действий по данной теме;
-
продолжить формирование практических навыков по теме.
Воспитательные:
-
формировать коммуникативные, социальные (работа в команде) навыки;
-
воспитывать личную ответственность;
-
развивать умение оценивать деятельность;
-
формировать эстетические навыки при выполнении чертежей.
Развивающие:
-
развивать способности к анализу, обобщению, систематизации;
-
развивать познавательную деятельность учащихся;
-
развивать интуицию, пространственное воображение.
Оборудование для организации урока:
-
компьютер, мультимедийный проектор, экран;
-
раздаточный материал;
-
листы оценки, ватман, листы белой бумаги А4,маркеры, фломастеры.
Структура урока:
-
Организационный момент (1 мин )
-
Сообщение темы и цели урока (1 мин )
-
Воспроизведение опорных знаний учащихся. (10 мин)
-
Обобщение и систематизация знаний по теме теме и их применение в стандартной ситуации (12 мин)
-
Оперирование ЗУН в нестандартной ситуации. (12 мин)
-
Итоговое обсуждение. Составление опорного конспекта. (5 мин)
-
Оценка работы. (3 мин)
-
Постановка домашнего задания. (1 мин)
Ход урока
-
№ п/п
Содержание этапа
Время
Деятельность учителя
Деятельность учащихся
Приложения, замечания
1
Организационный момент.
1 мин
Проверяет готовность класса к уроку: «Добрый день, ребята ! Давайте улыбнемся и подарим друг другу хорошее настроение».
Учащиеся рассаживаются по группам по 6 человек в каждой.
2
Постановка цели.
1 мин
Сообщает дату, тему и цель урока: « Сегодня на уроке мы должны не только обобщить наши знания, умения и навыки по данной теме в решении стандартных и нестандартных задач, но и представить эти знания в виде опорной схемы или таблицы».
Записывают в тетрадях.
В приложениях приводится возможное решение задачи, варианты возможны и приветствуются.
3
Воспроизведение опорных знаний учащихся.
10 мин
Вызывает к доске по 1 учащемуся из каждой группы
Учитель читает задачи и демонстрирует рисунки с помощью проектора. Во время обсуждения решения помогает в выборе более рационального, требует полных, доказательных рассуждений, оперированием теоретических знаний.
У доски выполняют задания по карточкам на построение ортогональных проекций куба.
Ученики отвечают на них по следующему принципу: сначала отвечает ученик из 1 группы. При правильном ответе балл идёт в счёт данного ученика и в копилку команды. Если же ответ неправильный, то право отвечать переходит к следующей команде и т.д.
Приложение 1. Рисунки будут использоваться на 5 этапе работы
Приложение 2.
Промежуточное подведение итогов решения опорных задач
Проверка правильности построения проекций
4
Обобщение и систематизация знаний по теме и их применение в стандартной ситуации
12 мин
Предлагает для решения стандартные задачи. Консультирует группы.
Каждая из команд получает по задаче и решает её в течение некоторого времени. Затем каждая группа по очереди у доски представляет решение своей задачи всему классу, причём каждый член группы должен отвечать за какой-то конкретный этап решения задачи. Например, первый ученик анализирует условие задачи, второй – представляет рисунок (чертёж, график к задаче), третий – её решение, четвёртый – анализирует полученное решение. После того, как группа представила решение своей задачи, группы-соперники задают вопросы. В конце второго этапа ученики перечисляют методы решения задач, а также отмечают особенности каждого метода.
Приложение 3
Промежуточное подведение итогов решения стандартных задач
5
Оперирование ЗУН в нестандартной ситуации
12 мин
Помогает в обсуждении предложенных решений.
Каждая команда получает по задаче, в решении которых используется ортогональное проектирование. Через некоторое время группы вновь представляют решение всему классу. Так же, как и на предыдущем этапе, каждый ученик несёт личную ответственность за успех своей группы. В конце третьего этапа ученики делают выводы, обобщая полученные в ходе исследований результаты.
Приложение 4
Промежуточное подведение итогов решения нестандартных задач
6
Подведение итогов
5 мин
Вместе с учащимися анализирует работу групп. С помощью проектора демонстрируется опорная схема.
Составляют на ватманах опорные схемы по теме, представляют их классу.
7
Оценка работы
3 мин
Вместе выводят итоговые оценки по результатам деятельности на уроке. ученики после каждого этапа урока на специальных бланках должны оценить свою деятельность, деятельность членов своей группы.
Приложение 5
8
Постановка домашнего задания.
1 мин
Комментирует.
Записывают. Используя полученные ЗУН по теме, самостоятельно составить и решить 3 различного типа задачи.
Приложение 5.
Оценочный бланк.
| устная работа | стандартная задача | нестандартная задача | конспект | оценка учителя | Средняя оценка | |||||
| самооценка | оценка группы | самооценка | оценка группы | самооценка | оценка группы | самооценка | оценка группы | |||
| | | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
Приложение 1.
Карточки для решения у доски
1 группа. Спроектируйте куб ABCDA1B1C1D1на плоскость, проходящую через точку В и перпендикулярную ВС1.

2 группа. Спроектируйте куб ABCDA1B1C1D1на плоскость, проходящую через точку A и перпендикулярную AD1

3 группа. Спроектируйте куб ABCDA1B1C1D1на плоскость, проходящую через точку D и перпендикулярную DC1

4 группа. Спроектируйте куб ABCDA1B1C1D1на плоскость, проходящую через точку C и перпендикулярную CВ1

Приложение 2.
Задачи для устного решения.
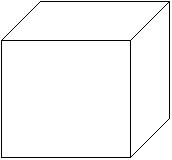
1. Верно ли, что прямая D1C1 пересекает прямую EF? Ответ объясните.

 B1C1
B1C1
A1 D1
 E
E
F

 В С
В С
А D
Решение. нет, неверно, так как D1C1 пересекает плоскость В1ВС1С, содержащую прямую EF, в точке не принадлежащей этой прямой. Следовательно, эти прямые – скрещивающиеся.
2. Точки А,К,С не лежат на одной прямой. Выясните взаимное расположение прямых АС и КС.
Решение. Так как точки не лежат на одной прямой, они лежат в одной плоскости. А поскольку прямые АС и КС имеют общую точку С, они пересекаются.
3. Прямые а и b скрещиваются с прямой с. Что можно сказать о прямых а и b?
Решение. Возможны три случая:
Прямые а и b пересекаются
 с
с
П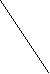 рямые а и b параллельны
рямые а и b параллельны
Прямые а и b срещиваются
с

 в
в



 а с
а с

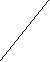 а в
а в


 в
в
а
4. Прямая с, параллельная прямой а, пересекает плоскость β. Прямая b принадлежит этой плоскости.. Верно ли, что
а) прямые b и с пересекаются; б) прямая а лежит в плоскости β; в) прямые b и а скрещиваются.
Решение. а) могут пересекаться или скрещиваться, б) а пересекает β, в) могут пересекаться или скрещиваться.
5. ABCDA1B1C1D1 – куб. Найдите угол между диагоналями В1С и DC1 .
Решение. По свойству параллельного переноса угол между диагоналями В1С и DC1 равен углу между АВ1 и В1С. Треугольник АВ1 С – равносторонний. Искомый угол равен 600.
6. ABCDA1B1C1D1 – куб с ребром а. Найдите угол и расстояние между прямыми D1D и ВC.
Решение. Угол определяется аналогично и равен 900. Расстояние – есть общий перпендикуляр к скрещивающимся прямым, это длина ребра CD= а.
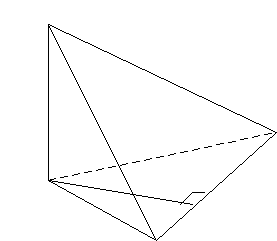
7. В треугольной пирамиде ABCD ребро CD перпендикулярно плоскости основания. Найдите расстояние между прямыми CD и АВ, если АС = 12 см, угол А равен 300
D
A
C
H
B
Решение: По условию прямая CD проецируется в точку C, а прямая АВ сама в себя. Значит, длина перпендикуляра СН и есть расстояние между скрещивающимися прямыми CD и АВ.
8. В основание цилиндра радиуса 2 см. вписан равнобедренный треугольник АВС с прямым углом В . Найдите угол и расстояние между образующей цилиндра ВВ1 и гипотенузой треугольника.
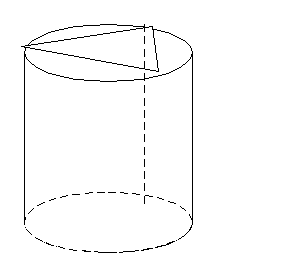
A B
C
B1
Решение. Из условия АС – диаметр, ВВ1 перпендикулярна плоскости основания цилиндра. Тогда ВВ1 и АС- скрещивающиеся прямые. Угол между ними 900, а расстояние = радиусу = 2см.
Приложение 3.
Применение ЗУН в стандартной ситуации.
1 группа.
В правильной четырехугольной призме ABCDA1B1C1D1 Е и F - середины ребер AD и CD соответственно. Найдите угол между прямыми B1D и EF.
Решение. EF - средняя линия треугольника АСD, она параллельна диагонали АС, которая перпендикулярна BD. Значит, по теореме о трех перпендикулярах B1D ┴ EF, угол между ними 900.
2 группа.
В правильной треугольной призме ABCA1B1C1 M, N, E - середины ребер АС, АВ, и ВС соответственно. Найдите угол между прямыми А1Е и MN.
Решение. MN - средняя линия треугольника АСВ, она параллельна ВС, которая перпендикулярна AE. Значит, по теореме о трех перпендикулярах А1Е ┴ MN, угол между ними 900.
3 группа.
В правильной четырехугольной призме ABCDA1B1C1D1 площадь основания равна 16 см2. Найдите расстояние между прямыми AA1 и B1D.
Решение. ABCD ┴ AA1 , прямая AA1проецируется в точку А, прямая B1D - в
прямую BD. АО - расстояние между данными проекциями и между прямыми AA1 и B1D. АО = 2√2 см.
4 группа.
Цилиндр радиуса ![]() см. вписан в правильную четырехугольную призму
см. вписан в правильную четырехугольную призму
ABCDA1B1C1D1. Найдите расстояние между осью цилиндра и диагональю C1D
Решение. ABCD ┴ ОО1 (ось цилиндра), прямая ОО1 проецируется в точку О, диагональ С1D - в СD. ОН - расстояние между данными проекциями и между прямыми ОО1 и С1D. АН = 3√5 см.
Приложение 4.
Применение ЗУН в нестандартной ситуации.
1 группа. Найдите угол и расстояние между диагоналями ВС1 и AB1 куба ABCDA1B1C1D1 с ребром 1.
2 группа. Найдите угол и расстояние между диагоналями AD1 и A1B куба ABCDA1B1C1D1 с ребром 1.
3 группа. Найдите угол и расстояние между диагоналями DC1 и B1C куба ABCDA1B1C1D1 с ребром 1.
4 группа. Найдите угол и расстояние между диагоналями CВ1 и A1B куба ABCDA1B1C1D1 с ребром 1.
Замечание. Используется проектирование на плоскость, перпендикулярную одной из скрещивающихся прямых. Причем, проекции у групп уже готовы, это задание по карточкам в начале урока. Задача учащихся увидеть, что в данной ситуации это самый рациональный способ.
Расстояние =1/√3, угол = 600.
Здесь представлен конспект к уроку на тему «Угол и расстояние между скрещивающимися прямыми», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Геометрия (10 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

