Презентация "Теория множеств" по математике – проект, доклад
Презентацию на тему "Теория множеств" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 38 слайд(ов).
Слайды презентации
Список похожих презентаций
Теория бесконечных множеств
Теорема 2. Отношение равномощности есть отношение эквивалентности. Доказательство. Необходимо проверить три условия: рефлексивность, симметричность, ...Теория конечных множеств (комбинаторика)
Если конечное множество A состоит из m элементов, то мы будем писать: |A| = m или n(A) = m. Теорема 1 (принцип сложения). Пусть A B = . Тогда n(A ...Теория вероятности в школе
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. Знание закономерностей, которым подчиняются массовые случайные ...Теория вероятности
Автор проекта ученица 10 класса «А» ГОУ СОШ № 420 г. Москвы Лавренова Юлия Руководитель проекта учитель математики ГОУ СОШ № 420 г. Москвы Афанасьева ...Пересечение и объединение множеств
Проверь себя. Море Берег Острова Волна Шторм Камень Океан Пляж. Игра « КОНТРПРИМЕР». Придумай предложение, которое по смыслу отрицает данное предложение:. ...Теория случайностей
Актуальность выбора темы моей работы объясняется тем, что в настоящее время теория вероятностей пользуется всё большей популярностью – её вводят как ...Теория графов
Что такое теория графов? Теория графов – это раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество ...Теория вероятности события
Введение в комбинаторику. В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать ...Сравнение множеств
. =. . 5 >. Множество круглых предметов. Множество желтых предметов. Множество съедобных предметов. 4 8. Домашнее задание стр. 11. упр. 22(г) стр. ...Практические занятия по дисциплине "Теория принятия решений"
Практические занятия по дисциплине «Теория принятия решений». Призваны закрепить знания теоретических вопросов, получить практические навыки решения ...Пересечения множеств
Проверь себя: задание5 задание7. . Волшебное слово НЕ. «НЕ страна» «НЕ город». Задание № 9. Задание № 10. Игра "Что на пересечении?". Пересекаются ...Пересечение множеств
Витя начертил фигуры и раскрасил их синим и красным цветом. Какая фигура является их пересечением (общей частью)? Назовите элементы пересечения множеств ...Пересечение и объединение множеств
1.Пересечение множеств. А- множество натуральных делителей числа 24, В- множество натуральных делителей числа 16. А={1,2,3,4,6,8,12,24}, В={1,2,3,6,9,18}, ...Пересечение и объединение множеств
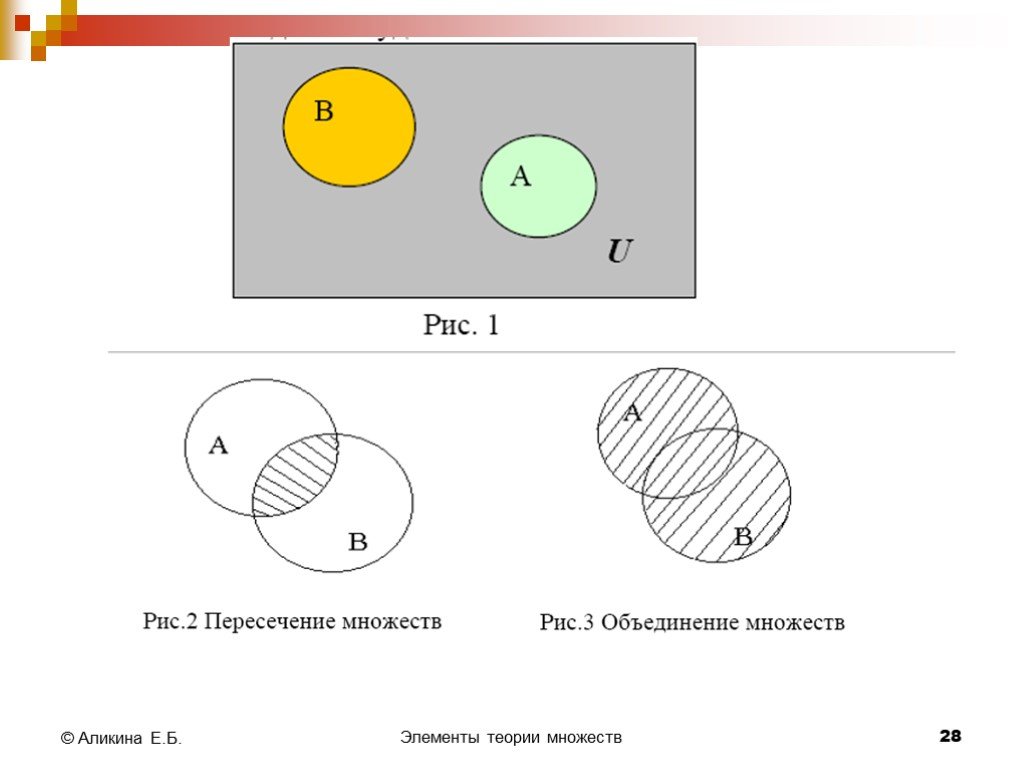
АЛГЕБРА 8 класс. «Пересечение и объединение множеств». Тема урока:. Пересечением двух множеств называют множество, состоящее из всех общих элементов ...Теория вероятности и статистика
Определение. Пусть А и В – два события, относящиеся к одному случайному опыту. Взяв все элементарные события, которые благоприятствуют и событию А, ...Теория вероятности и статистика
Вероятность и статистика. Вероятностно-статистические закономерности изучает специальный раздел математики – теория вероятности. Теория вероятностей ...Теория вероятностей
№ 1. В кармане у Миши 4 конфеты – «Грильяж», «Маска», «Белочка», «Красная шапочка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил ...Теория графов
V={A,В,С,D,F,Н,P} – множество точек, E={a,b,с,d,e,f,g,h,p,l} – множество линий f: Е→ V&V, определяется по закону f: a→(H&H), b→(P&F), c→(B&C), d→(A&B), ...Теория вероятностей в нашей жизни
Достоверные, случайные и невозможные события. Достоверное событие – событие, которое в данном опыте обязательно наступит. Случайное событие – событие, ...Теория катастроф
Теория катастроф. Теория катастроф — раздел математики, включающий в себя теорию бифуркаций дифференциальных уравнений (динамических систем) и теорию ...Конспекты
Теория вероятностей
МБОУ «СОШ № 143» г. Красноярска,. . учитель математики Князькина Татьяна Викторовна. Теория вероятностей: подготовка к ЕГЭ 2014. Не так ...Теория вероятностей и комбинаторика в заданиях ЕГЭ
ШЕВЕЛЕВА НАДЕЖДА. МИХАЙЛОВНА. МОУ «Ягельная СОШ» Надымского района. Ямало-Ненецкого автономного округа. Учитель математики. ...Объединение множеств
Муниципальное общеобразовательное учреждение. . «Средняя общеобразовательная школа № 3 г. Козьмодемьянска». Республики Марий Эл. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:11 ноября 2018
Категория:Математика
Содержит:38 слайд(ов)
Поделись с друзьями:
Скачать презентацию

















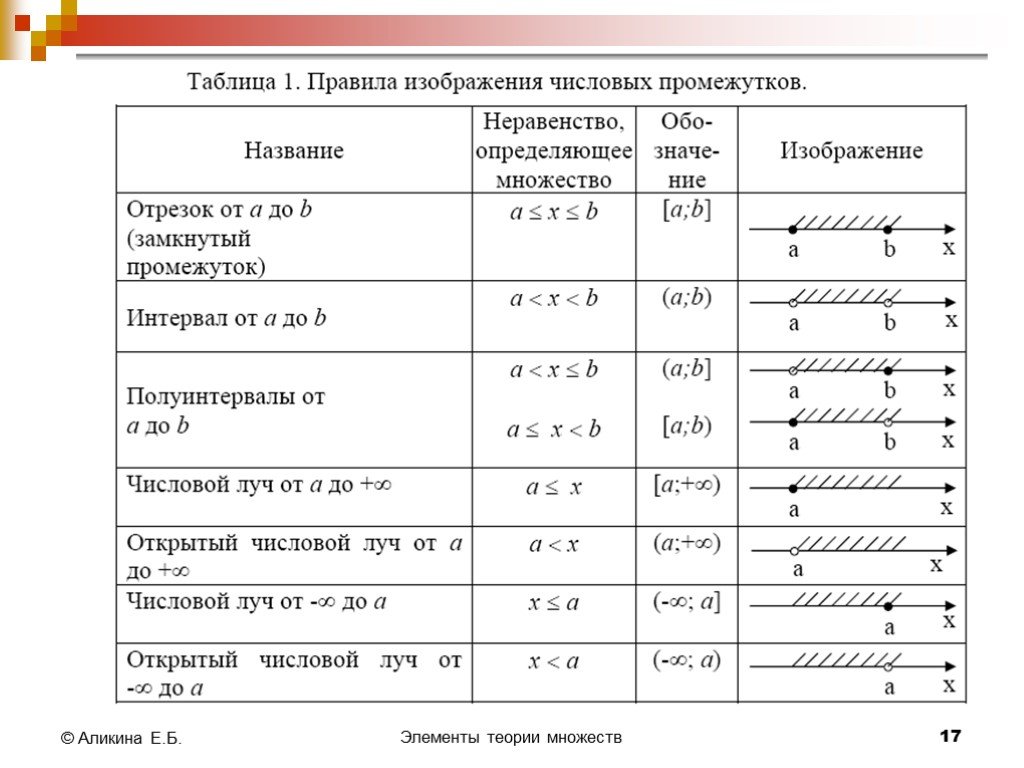



























![Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: В⊄А. Например, отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. а[а, b], но а∉(а, b]. Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: В⊄А. Например, отрезок [а, b] не является подмножеством полуинтервала (а, b], т.к. а[а, b], но а∉(а, b].](https://prezentacii.org/upload/cloud/18/11/99394/images/thumbs/screen12.jpg)
























































