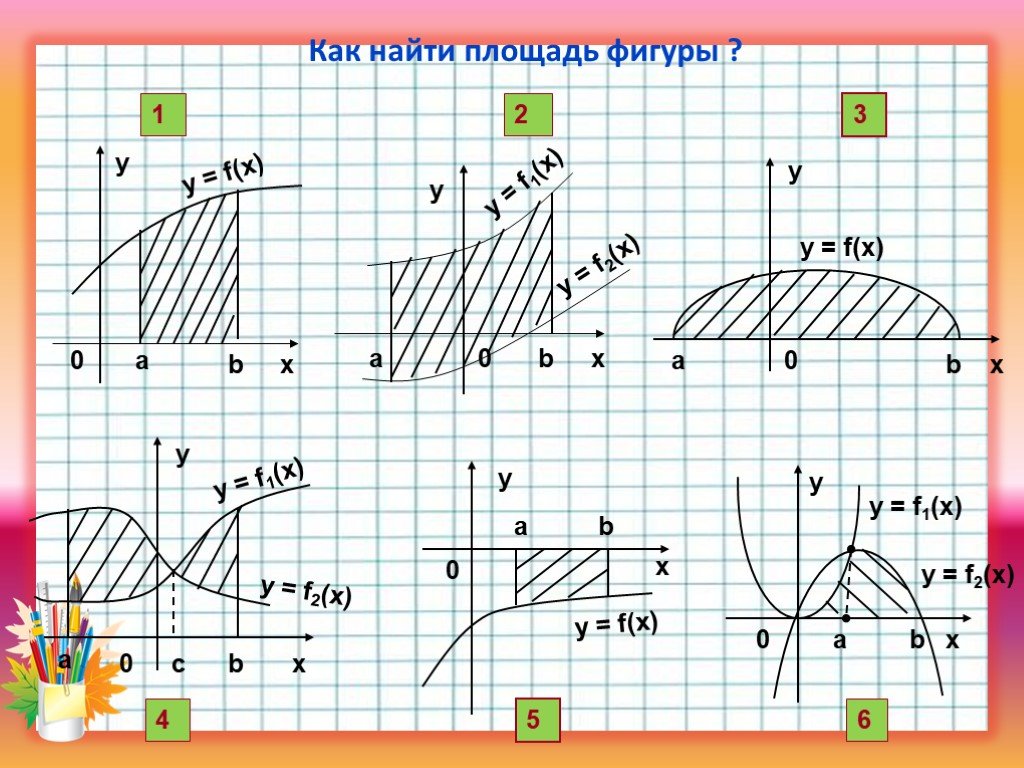
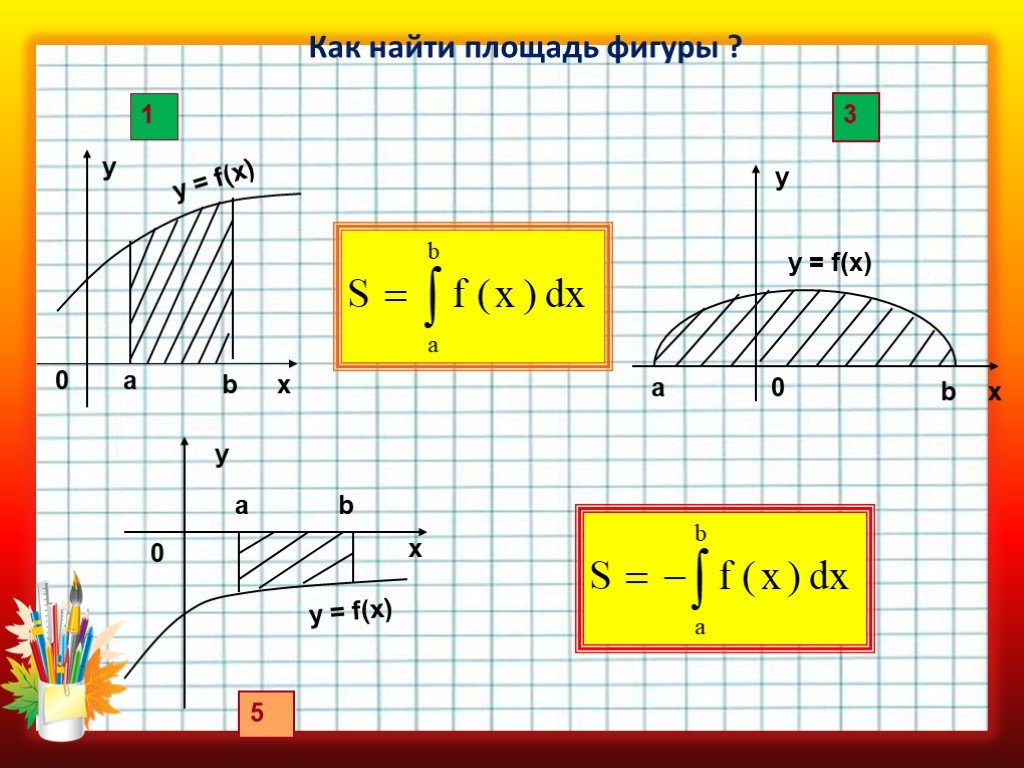
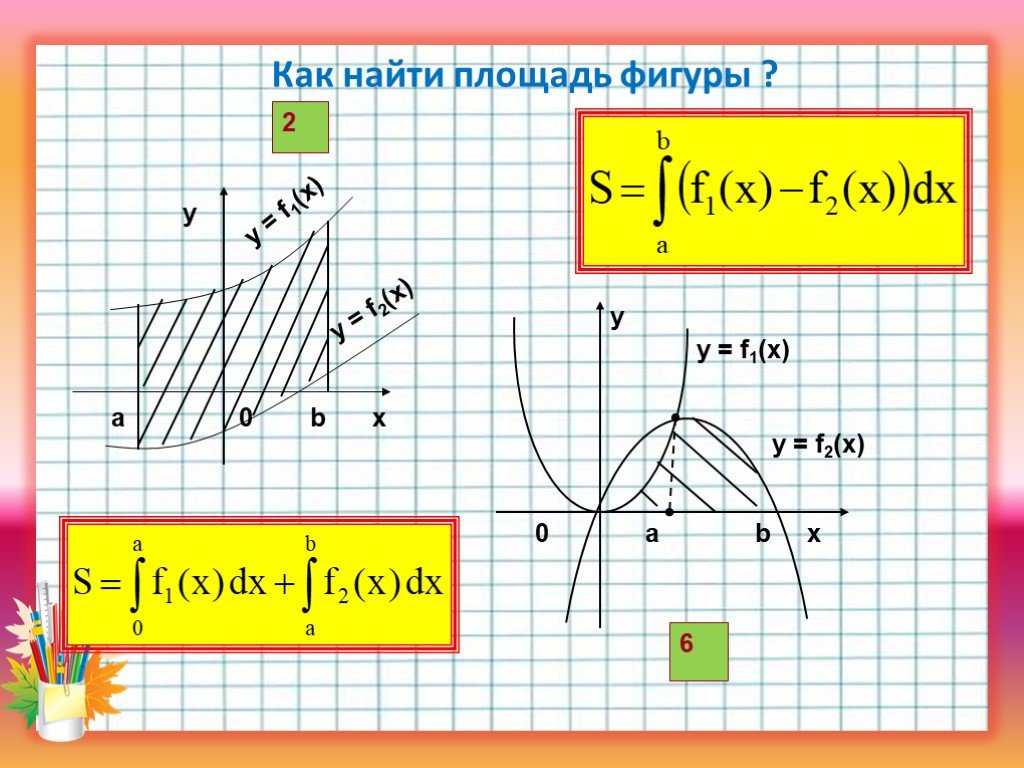
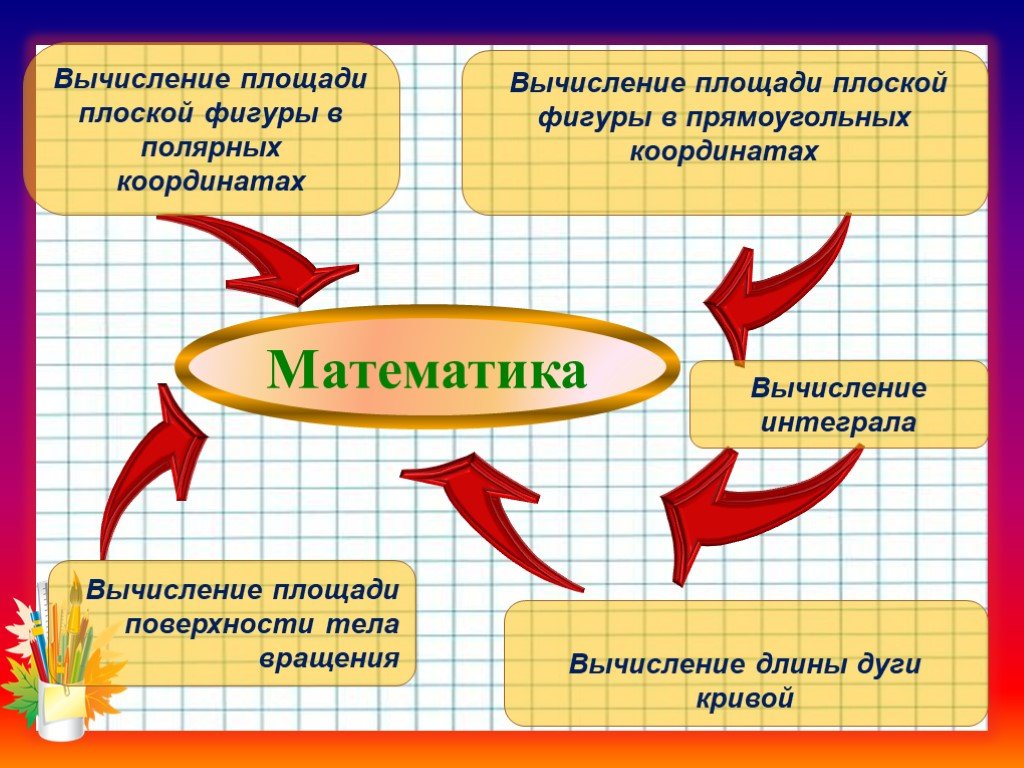
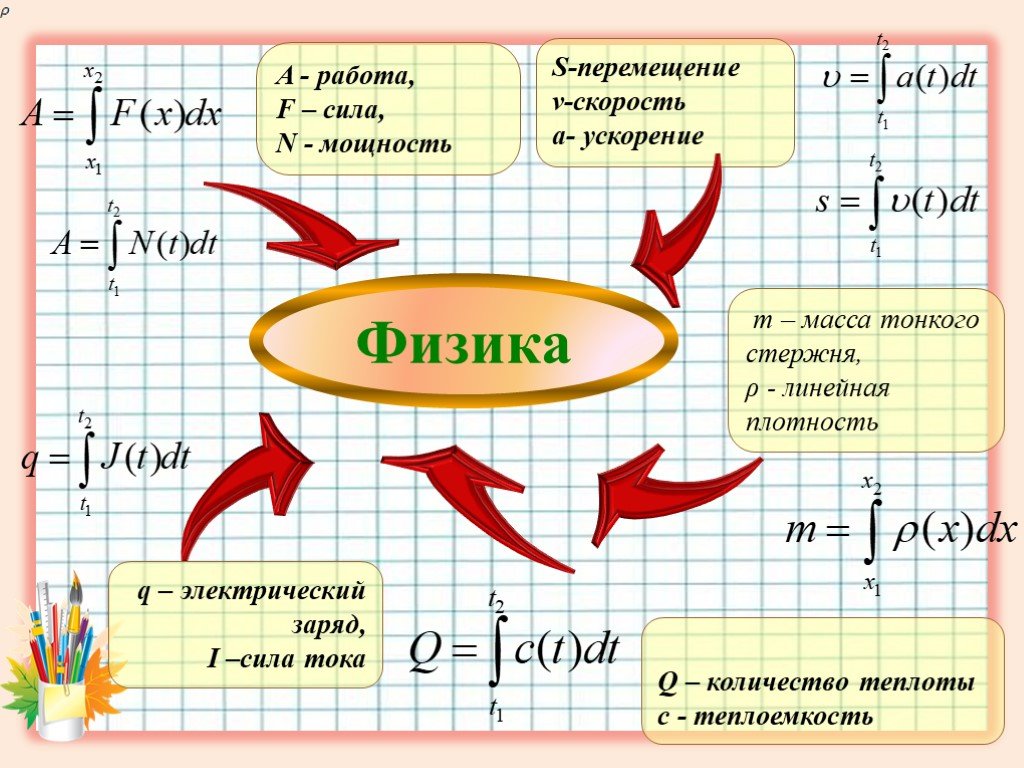
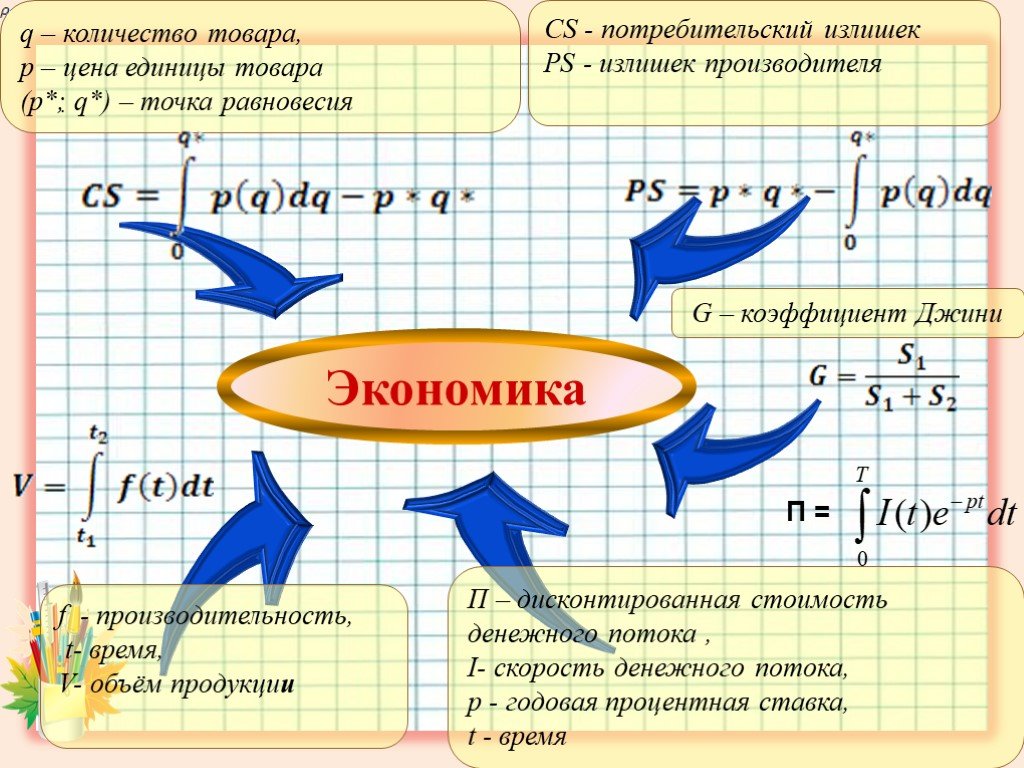
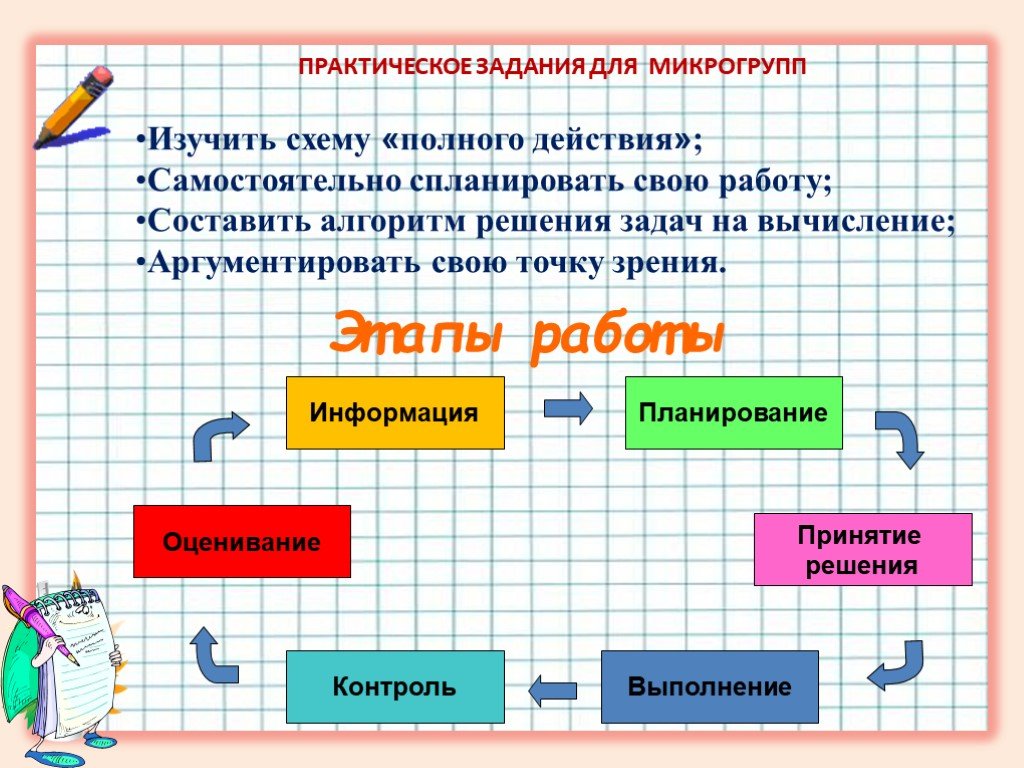
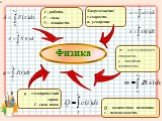
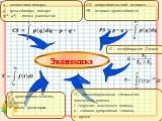
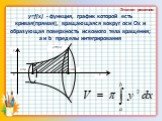
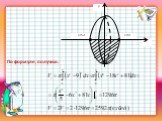
Презентация "Применение определенного интеграла при решении прикладных задач" по математике – проект, доклад
Презентацию на тему "Применение определенного интеграла при решении прикладных задач" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 30 слайд(ов).
Слайды презентации
Список похожих презентаций
Арифметическая и геометрическая прогрессии при решении задач
с и п о г р я е. ПРОГРЕССИЯ. арифметическая аn+1=аn+ d an= a1+d(n-1). геометрическая bn+1= bn * q bn= b1*qn-1. Арифметическая и геометрическая прогрессии ...Графы и их применение к решению задач
Как известно, умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Поэтому ...Выбор действий при решении задач
Прочитай вопрос и выбери действие. Приношу свои извинения, но придётся начать заново! - · : +. На сколько 25 больше 5? У Лены 5 игрушек. У Вали в ...Дополнительные построения в трапеции при решении задач
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции ...Вычисление площадей плоских фигур с помощью определенного интеграла
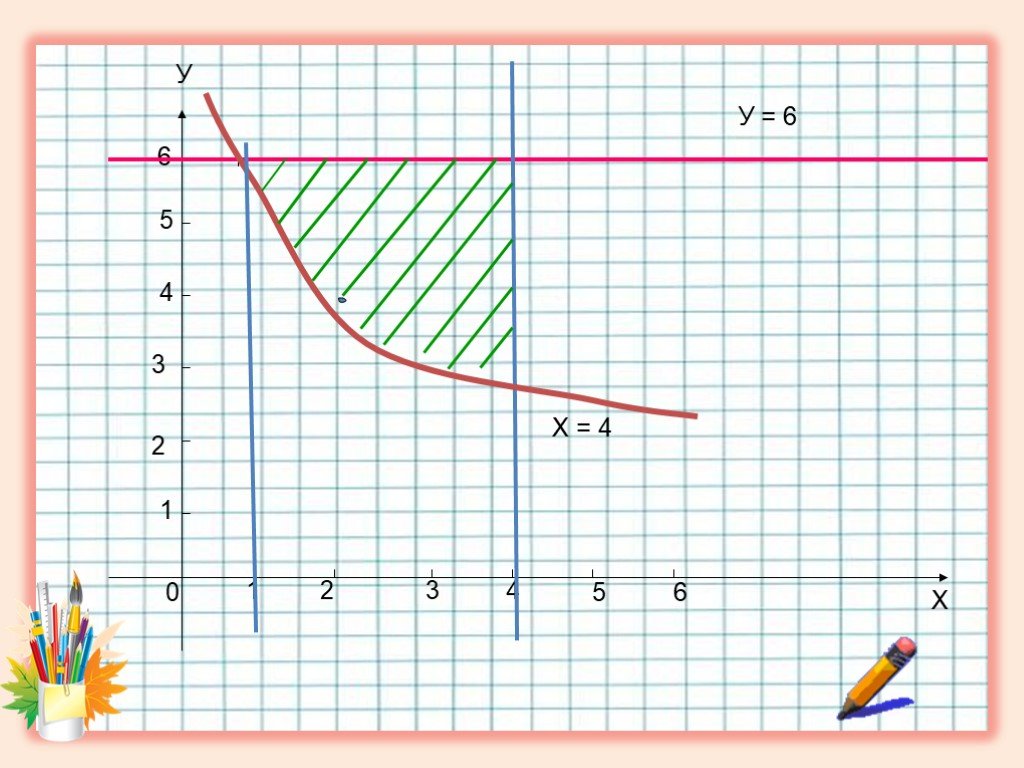
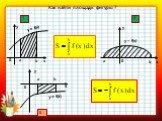
ВЫЧИСЛИТЕ ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ И ВЫ УЗНАЕТЕ ОДНО ИЗ ВЫСКАЗЫВАНИЙ ФРАНЦУЗСКОГО МАТЕМАТИКА С.Д.ПУАССОНА. Жизнь украшается двумя вещами: занятием математикой ...Вычисление площадей плоских фигур с помощью определенного интеграла
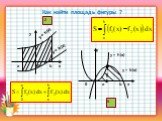
Плоские фигуры a b y = f(x) y = g(x). Р M K C D. . Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x, y = 5 – x, x = 1, x = 2. 0 1 2. ...Графические приемы решения задач с параметрами
Решение уравнений и неравенств, содержащих параметры, является одним из самых трудных разделов элементарной математики. Для их решения обычно требуются ...«Решение задач с помощью пропорций»
Найти значение Х: Х:3=4:6 5:Х=2:6 7:3=Х:18 Устная работа. Указать вид пропорциональной зависимости:. Какова зависимость пути от времени? Какова зависимость ...Вычитание. Решение задач с помощью действия вычитания
Определение целей урока. Чему должны научиться сегодня на уроке? Какими свойствами вычитания будем пользоваться? Что нужно будет знать, чтобы решить ...ГИА-2012. Решение планиметрических задач на нахождение углов геометрических фигур
1 3 4 5 6 7 8 9 10 11. Вашему вниманию представлено двенадцать прототипов задачи № 11 Открытого банка заданий по математике. ГИА – 2012. Два острых ...Алгоритм решения задач на пропорции
Эпиграф: «Математика обладает двумя великими сокровищами. Первое-это теорема Пифагора, второе-деление отрезка в крайнем и среднем отношении.» Иоганн ...Алгоритм решения простых задач
. ЗАДАЧА условие Вопрос, задание. Работа в парах. 1. Налетело 5 гусей-лебедей, подхватили и унесли братца Иванушку. 2. Печка испекла девять ржаных ...Алгебра высказываний. Решение логических задач
Задача 1: Составьте сложное высказывание в словесной форме из простых, заданных математическим формулировкам:. Высказывание А: «Учащийся Иванов хорошо ...Алггоритм. Решение задач
Задача 1. В урне хранится некоторое количество чёрных и белых шаров. Требуется разложить эти шары по двум корзинам чёрного и белого цвета: белые шары ...Активизация познавательной деятельности при обучении математике
. Народная Классическая Педагогическая Цирковая (эстрадная) Спортивная. Группировка Классификация Систематизация Ассоциация Аналогия Рифмитизация ...Аксиомы стереометрии Решение задач
Через любые две точки пространства проходит единственная прямая. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная ...Аксиомы стереометрии и их следствия. Решение задач
Цель урока: обобщение и применение аксиом и их следствий к решению задач. Математический диктант. 1). Сформулируйте аксиомы стереометрии: Аксиома ...ГИА-2012. Решение задач по теме "Чтение графиков функций"
График какой из приведенных ниже функций изображен на рисунке? Задание 17 (№ 197785). Задание 17 (№ 193087). Задание 17 (№ 197695). Задание 17 (№ ...Ассоциация, как помощник, при изучении математики
Ассоциация- это мысленная связь между двумя образами. Чем многообразнее и многочисленнее ассоциации, тем прочнее они закрепляются в памяти. Странные, ...Конспекты
Закрепление вычислительных навыков при решении нестандартных задач
Урок математики в 4-м классе. Тема: ". . Закрепление вычислительных навыков при решении нестандартных задач". . . . Автор: Витязева ...Вычисление площадей плоских фигур с помощью определенного интеграла
7. . . Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа с. Успеновка. ...Web -разработка. Применение производной.10 класс
ТЕХНОЛОГИЧЕСКАЯ КАРТА КОНСТРУИРОВАНИЯ УРОКА С ИСПОЛЬЗОВАНИЕ СРЕДСТВ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ. Учитель Беломестнова Наталья Петровна. Предмет, ...Геометрический смысл производной. Применение производной к исследованию функций
Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций». Цель урока. :. содействовать созданию ...Геометрический и физический смысл производной. Применение производной
Учитель математики. КГУ «Экономический лицей». Воробьева. Ирина. Юрьевна. Методическая разработка. урока математики в 10 классе. « Геометрический ...Закрепление первоначальных приёмов умножения. Решение обратных задач
Открытый урок по математике во 2 «б» классе,. учитель Заруба Наталья Сергеевна. средняя школа № 96 г. Краснодар. Тема: Закрепление первоначальных ...Закрепление решения примеров и задач в пределах 20
Муниципальное казенное специальное (коррекционное) образовательное учреждение для обучающихся, воспитанников с ограниченными возможностями здоровья ...Закрепление решения примеров, простых и составных задач на табличное умножение и деления до 5
Абросимова Марина Владимировна. МБОУ «СОШ№1» г. Топки. . . Учитель начальных классов. Урок математики 3 класс. . Тема. ...Закрепление изученного материала. Решение задач и примеров в пределах 100.
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа № 64 ». города Астрахани. Конспект урока ...Закрепление: умножение и деление многозначных чисел на однозначные, решение уравнений и задач на движение
Урок математики в 4 классе. Урок-сказка закрепления пройденного материала. Тема: «Закрепление: умножение и деление многозначных чисел на однозначные, ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:4 октября 2018
Категория:Математика
Содержит:30 слайд(ов)
Поделись с друзьями:
Скачать презентацию