Презентация "Плащадь трапеции" по математике – проект, доклад
Презентацию на тему "Плащадь трапеции" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 14 слайд(ов).
Слайды презентации
Список похожих презентаций
Свойства трапеции
Какой четырехугольник называется трапецией? Ответ: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. ...Площадь трапеции
Трапеция. ВС параллельна АД, АВ не параллельна СД МN – средняя линия трапеции MN параллельна АД и СД АС и ВД - диагонали трапеции Если АВ=СД, то трапеция ...Площадь: площадь трапеции
Определение трапеции:. В А С D. АD // ВС, АВ и СD – непараллельные отрезки. Трапецией называется четырёхугольник, у которого только две противолежащие ...Площадь трапеции
Цели урока. I.Образовательные цели урока: 1.Ввести формулу площади трапеции; 2.Закрепить навыки её использования с помощью задач; II .Развивающие ...Площадь трапеции
Площадь трапеции 8 класс. Трапеция и её элементы:. А В С D H О a b c d d1 d2. Свойства: Площадь фигуры равна сумме площадей ее частей 2.Высота трапеции ...Вычисление площади криволинейной трапеции
Тема урока:. криволинейной трапеции». «Вычисление площади. Цели урока. 1. Найти способы решения задач различного уровня сложности 2. С помощью знаний ...Площадь трапеции
А В С D a b h. 8 5 О х 12 h = 8. Домашнее задание Вопросы 1 – 6. Задачи № 37, 40. ...Площадь криволинейной трапеции и интеграл
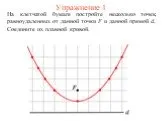
Криволинейная трапеция. Отрезок [a;b] называют основанием этой криволинейной трапеции. Криволинейной трапецией называется фигура, ограниченная графиком ...Площадь параллелограмма, треугольника, трапеции
Вычисление площадей фигур на клетчатой бумаге.1 3 4 5 6 7 8 9 10 11. Найдите площадь фигуры:.
Ответ: 6 см² №1. №2. 12 см² №3. №4. 28 см² №5. №6 ...
Площадь криволинейной трапеции
Площадь криволинейной трапеции. y x B C D A a b Y = f(x) s. ABCD –криволинейная трапеция. S = F(b) – F(a) F/ (x) = f(x). Y=g(x). Записать формулу ...Площадь криволинейной трапеции
Вычислить площадь криволинейной трапеции. ...Найти площадь криволинейной трапеции
Определение производной:. Найти производную функции по определению:. Вставьте вместо *. Определение первообразной:. Будут ли первообразными следующие ...Интеграл. Площадь криволинейной трапеции
Цели и задачи урока: Обобщить и систематизировать теоретический материал по теме. Отработать навыки вычисления первообразных для функций. Отработать ...Дополнительные построения в трапеции при решении задач
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции ...Средняя линия трапеции
Трапеция – это четырехугольник , у которого две стороны параллельны , а две другие стороны не параллельны.Определение. Определение средней линии ...
Площадь трапеции
Игра «Угадай формулу». Площадь трапеции равна произведению полусуммы её оснований на высоту. H H1. Дано: ABCD – трапеция AD и BC основания, BH – высота ...Трапеция. Виды трапеции
Трапеция. от греч. trapeza — стол. Трапеция буквально — «столик». Геометрическая фигура была названа так по внешнему сходству с маленьким столом. ...Трапеция. Свойства трапеции
Ответьте на вопросы. Из чего составлена данная геометрическая фигура? Какими должны быть треугольники, составляющие трапецию? Как составляются треугольники ...Вычисление площади криволинейной трапеции
Найти первообразную функции:. 1 задание 2 задание*. устно. 1. Какая фигура называется криволинейной трапецией? 2 3. Как найти площадь криволинейной ...Фракталы – геометрия природы
Задачи:. узнать, что такое «фракталы»; изучить историю возникновения и развития фрактальной геометрии; ознакомиться с биографией создателя фракталов ...Конспекты
Трапеция. Свойства трапеции
МБОУ гимназия № 12. . Ахонен Екатерина Петровна. . Геометрия. . 8 класс. . . Профильный уровень, используемые учебники: Геометрия: ...Средняя линия трапеции
Тема: "Средняя линия трапеции". . Цели урока:. 1. Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять ...Трапеция и средняя линия трапеции
Тема:. Трапеция и средняя линия трапеции. . Цели:. . . . а) повторить и закрепить знания по теме, формирование навыков решения задач на нахождение ...Площадь трапеции
государственное бюджетное общеобразовательное учреждение. Самарской области средняя общеобразовательная школа. «Образовательный центр». с. Старая ...Площадь трапеции
Урок геометрии в 8 классе. «. Площадь трапеции». Цели:. . Учить решать задачи с применением теоремы о площади трапеции. . . . Совершенствовать ...Площадь трапеции
МБОУ СОШ № 37 г. СМОЛЕНСК. Открытый урок геометрии в 8 классе. Тема: «Площадь трапеции». Учитель: Емельяненко ...Площадь трапеции
Технологическая карта урока геометрии в 8 классе по теме: «Площадь трапеции». подготовила учитель математики первой квалификационной категории. ...Площадь трапеции
Урок геометрии в 8 классе. Истляуп А.А., средняя общеобразовательная школа-гимназия №17 г.Актобе. Тема:. «Площадь трапеции». Цели урока:. ...Площадь трапеции
План – конспект урока по геометрии с использованием ЭОР. Автор:. Макарова Татьяна Павловна,. учитель высшей категории Государственного бюджетного ...Площадь трапеции
Проект урока по геометрии. Тема:. . «Площадь трапеции». Класс:. . 8а. Программа. Программы для общеобразовательных учреждений. Геометрия. ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:27 сентября 2019
Категория:Математика
Содержит:14 слайд(ов)
Поделись с друзьями:
Скачать презентацию