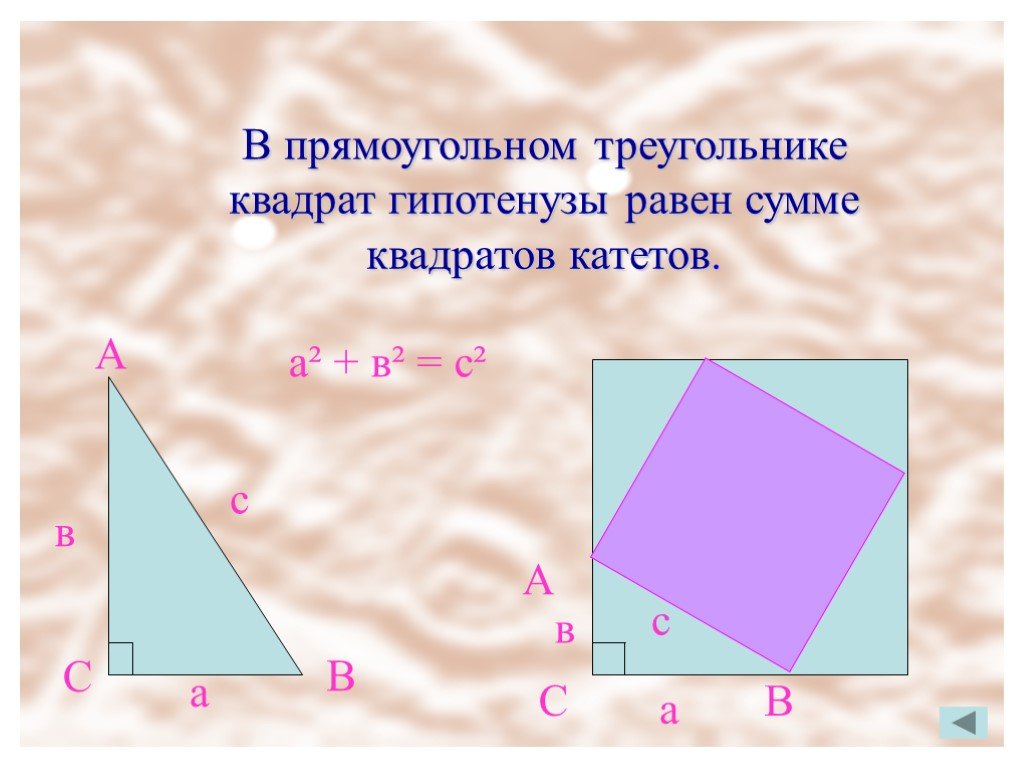
Презентация "Теорема Пифагора" по математике – проект, доклад

Смирнова Татьяна Григорьевна

Учитель математики, завуч школы №516

Теорема Пифагора

Формулировка теоремы Проверь себя Задачи с практическим содержанием Задачи Древнего Китая

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

А С а в В с а² + в² = с²

Задачи с практическим содержанием

1. Лестница длиной 13 метров приставлена к стене так, что расстояние до нижнего конца лестницы до стены равно 5 метров. На какой высоте от земли находится верхний конец лестницы?

Чертеж Решение 13 м h

h² = 13² - 5² h² = 144 h = 12 Ответ: 12 метров

2. Для установки мачты телевизионной антенны изготовлены тросы длиной 17 метров. Тросы крепятся на мачте на высоте 15 метров. На каком расстоянии от мачты надо укрепить концы троса?

17 м 15 м m

m ² = 17 ² - 15 ² m ² =64 m = 8 Ответ: 8 метров

3. Вертикальная мачта поддерживается четырьмя канатами, прикрепленными к ней на расстоянии 16 метров от земли и к земле на расстоянии 12 метров от основания мачты. Сколько метров каната потребовалось для укрепления мачты, если на узлы пошло 10 метров?

12 м 16 м

m ² = 16 ² + 12 ² m ² = 400 m = 20 20 · 4 +10 = 90 Ответ: 90 метров

4. Длина маятника АМ=1 м, высота его подъема при отклонении в точку В на некоторый угол равна СА=10 см. Найдите расстояние от точки В до прямой МА.

x ² = 100 ² - 90 ² x ² = 1900 x ≈ 43,6 Ответ: 43,6 см

1 подсказка: Рассмотреть прямоугольный треугольник МВС.

2 подсказка: Пусть ВС = х см. По условию МВ=100см, МС=90 см.

Пусть ВС = х см.

Задачи Древнего Китая

Наиболее ранние из дошедших до нас китайских математических текстов относятся к концу 1 тысячелетия до нашей эры. Основным научным трудом была «Математика в девяти книгах».Она предназначалась для всех, кому требовались математические знания: землемерам, чиновникам, инженерам, торговцам. По существу это сборник из 246 задач без вводных текстов и предварительных разъяснений. Каждый раз вначале формулируется задача, затем сообщается ответ и в сжатой форме указывается способ решения. Рассмотрим две задачи из девятой книги «Математики в девяти книгах».

Задача 6 Задача 13

Имеется водоем со стороной в 1 чжан (=10 чи). В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснется его. Спрашивается: какова глубина воды и какова длина камыша?

Ответ: глубина воды 12 чи, длина камыша 13 чи.

Пусть глубина воды х(смотри рисунок). Получим прямоугольный треугольник, у которого один катет х, второй катет 5, а гипотенуза х+1. Используем теорему Пифагора: х ²+5 ²=(х+1) ². Решим уравнение: х ²+25=х ²+2х+1 24=2х х=12

Имеется бамбук высотой в 1 чжан (=10 чи). Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня. Спрашивается: какова высота после сгибания?

Пусть высота бамбука после сгибания х (смотри рисунок). Получим прямоугольный треугольник, у которого один катет х, второй катет 3, а гипотенуза 10-х. Используем теорему Пифагора: х ²+3 ²=(10-х) ². Решим уравнение: х ²+9=100-20х+ х ² 20х=91 х = 4,55

Ответ: высота после сгибания 4,55 чи.

Спасибо за внимание! Надеюсь, что вам было интересно!