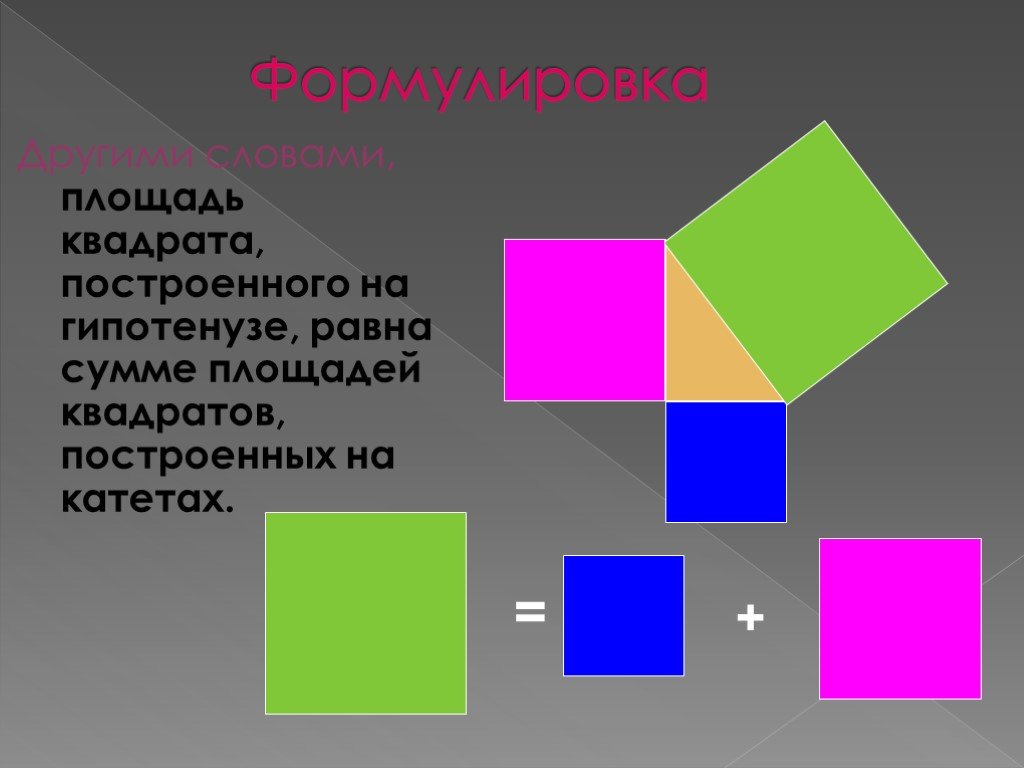
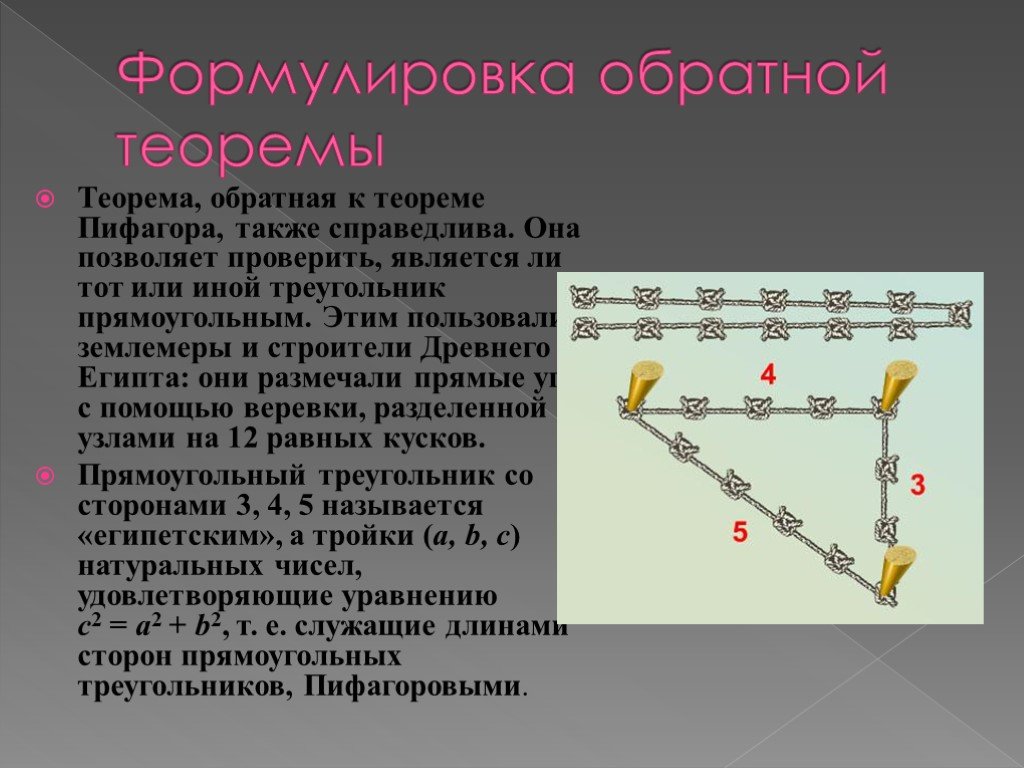
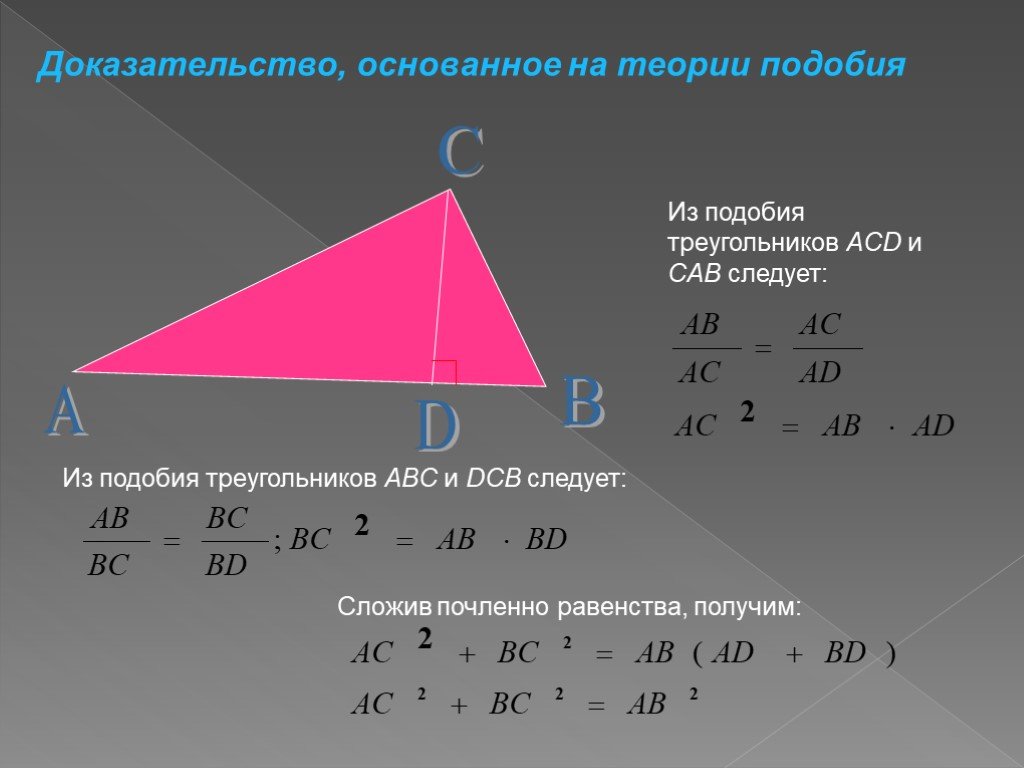
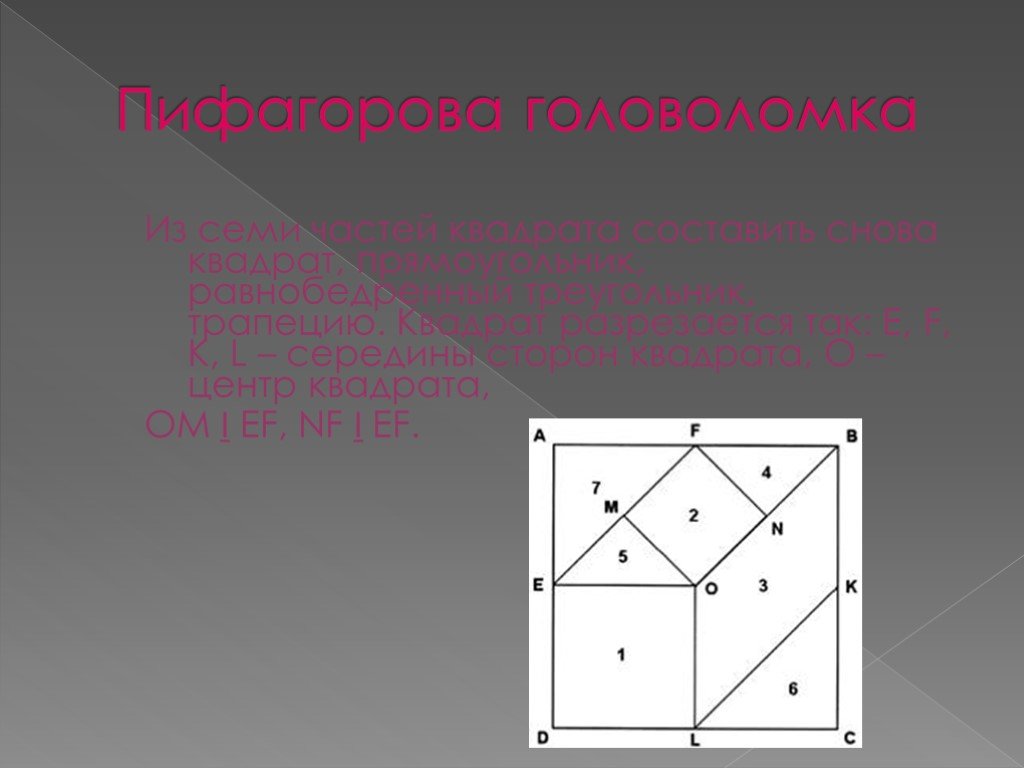
Презентация "Теорема Пифагора: числа и история" по математике – проект, доклад
Презентацию на тему "Теорема Пифагора: числа и история" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 23 слайд(ов).
Слайды презентации
Список похожих презентаций
«Моя математика» 1- класс - числа 0-10
Цели урока: Закрепить: навыки счета в пределах10; состав чисел 2-10; умение записывать числа арабскими и римскими цифрами; умение сравнивать выражения; ..."Взаимно обратные числа"
Цели урока:. ввести понятие взаимно обратных чисел; сформировать умение находить взаимно обратные числа при решении упражнений; повторить правило ...«Действия с дробями», «Нахождение дроби и процентов от числа»
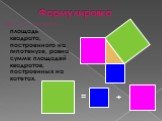
Систематизация знаний по темам: «Действия с дробями», «Нахождение дроби и процентов от числа», Отработка практических навыков выполнения действий ...Cпособы доказательства теоремы Пифагора
a2+b2=c2 c a b П. Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым ..."Целые числа и действия с ними". 6-й класс
«Сумма двух долгов есть долг». «Сумма имущества и долга равна их разности». (– 3) + (– 5) = – 8 4 + (– 7) = 4 – 7 = – 3. – 8 · (– 2) = 4; – 9 : (– ..."Умножение дробей, нахождение дроби от числа"
. Выполнить умножение: 3 8 ∙2=. Выполнить умножение: 3 7 ∙ 2 9 =. 2 21. Выполнить умножение: 5∙1 7 15 =. 7 1 3. Вычислить площадь квадрата со стороной ..."Смешанные дроби. Представление смешанного числа в виде неправильной дроби".
Смешанные дроби. Представление смешанного числа в виде неправильной дроби. 02.03. Определите координаты точек А, В, С и М. ..."Доли и дроби"
Семья Долиных:. Бабушка Доля Дедушка Доль Внуки Дробик и Долюша. Бабушка доля очень любит печь пироги. Дробик пришел с фермы очень голодный. разрезал ..."Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
1. Найти наибольшее значение функции по её графику на [ -5;6] и [-7; 6]. 5 4 -5 у наиб. = 4 [-5; 6] у наиб. = 5 [-7; 6] 1. 2. Найти наименьшее значение ...Аксиомы стереометрии и их простейшие следствия
Аксиомы стереометрии. 1)Какова бы ни была плоскость, существуют точки, принадлежащие ей и точки, не принадлежащие ей. 2) Если две плоскости имеют ...Авторские задачи по математике и физике, составленные по повести Н.В. Гоголя «Ночь перед Рождеством
Методологическая основа: Класс арифметических задач огромен. Учащиеся старших классов обычно пытаются решать такие задачи алгебраически, так как владеют ..."Сложение положительных и отрицательных чисел"
Старостенко Алла Николаевна, учитель математики Предмет: математика, урок-игра, закрепление изученного материала Тема: «Сложение положительных и отрицательных ...«Треугольники и их виды»
Геометрические фигуры. а ж е д с б и з. Треугольники и их виды. Определение треугольника, элементы треугольника Виды треугольников Сумма углов треугольника ...«Сложение положительных и отрицательных чисел».
. Кемеровская область. Если в картину Сибири всмотреться, На ней обозначены контуры сердца. И бьется оно. И отчизна внимает Рабочему ритму Кузнецкого ..."Число и цифра 9"
Число и цифра 9. Тема урока:. Цель урока:. познакомить с числом 9, обучить написанию цифры 9. Задачи урока:. вспомнить времена года, дни недели, месяцы; ..."Функция y = kx², ее свойства и график". 8-й класс
Траектория движения комет в межпланетном пространстве. Архитектурные сооружения. . Траектория движения. Тема урока. Функция у=кх2, ее график и свойства ..."Умножение и деление чисел"
Тема урока:. Умножение и Деление чисел. В наше время, чтобы строить И машиной управлять, Помни друг, что надо прочно Математику познать! Математический ..."Турнир веселых и смекалистых знатоков истории, физики, химии, математики"
Цели мероприятия: 1.Развитие у учащихся интереса к изучаемым предметам. 2.Показать необходимость знаний по математике в других науках. 3.Формирование ...«Решение задания С1 ЕГЭ по информатике и ИКТ»
2 балла. Решение задания С1 ЕГЭ по информатике и ИКТ. Кунина В.В. область I область II. 0 x y y = x+2 y2 + x2 = 25 y2 + x2 25 y 0 x 0 область ..."Электрики и математика"
Воспитательные Воспитание умения работать в команде, уважения к сопернику, воспитание чувства ответственности; Воспитание чувства ответственности, ...Конспекты
Взаимно простые числа
Математика – 6 класс. . Тема урока. : «Взаимно простые числа». Автор: Хамидуллин Алмаз Нуртдинович. . Учитель математики. . МБОШИ ...Взаимно простые числа
НОД. Взаимно простые числа. Цель урока:. закрепить знание о делителе числа, научить учащихся находить наибольший общий делитель, развивать вычислительные ...Взаимно простые числа
Разработана учителем математики МБОУ-СОШ №64 города Тулы Платоновой Наталией Сергеевной. . Разработка урока математики по технологической карте. ...Взаимно обратные числа
Урок 59. Взаимно обратные числа. Цели:. отрабатывать навык нахождения чисел, обратных данным,. умения. решать уравнения нового типа; формировать. ...Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число
Открытый урок математики 4 класс. Тема: Алгоритм письменного деления многозначного числа на двузначное, трёхзначное число. Цель:. формирование ...Арифметические действия с положительными и отрицательными числами
. Муниципальное бюджетное общеобразовательное учреждение«Лицей №2». Методическая разработка урокаматематики. «Арифметические действия ...Взаимно обратные числа
ПЛАН-КОНСПЕКТ УРОКА. . Взаимно обратные числа. . ФИО (полностью). . . Гаврилова Марина Александровна. . . . Место работы. ...Большие и малые числа в химии
МКОУ «Средняя общеобразовательная школва №5. . города Ершова Саратовской области». . Бинарный урок. Большие и малые числа в химии. Провели ...Арифметическая и геометрическая прогрессии
Ф.И.О автора материала. :. Дыда Татьяна Ивановна. Место работы. :. МАОУ СОШ № 18, г. Армавир, Краснодарский край. Должность. :. Учитель математики. ...В мир одночленов и многочленов
Алгебра 7 класс. Урок – путешествие «В мир одночленов и многочленов». Цели:. обеспечить повторение и систематизацию материала темы; создать ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 мая 2019
Категория:Математика
Содержит:23 слайд(ов)
Поделись с друзьями:
Скачать презентацию