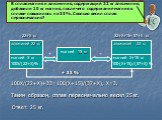
Презентация "Решение задач на смеси, сплавы, растворы" по химии – проект, доклад
Презентацию на тему "Решение задач на смеси, сплавы, растворы" можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Химия. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 9 слайд(ов).
Слайды презентации
Список похожих презентаций
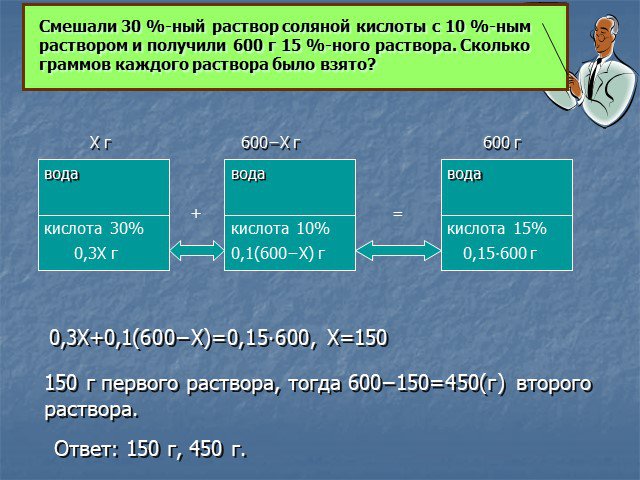
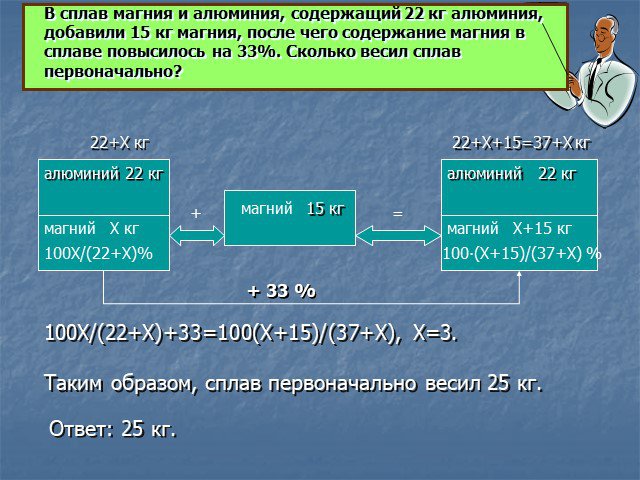
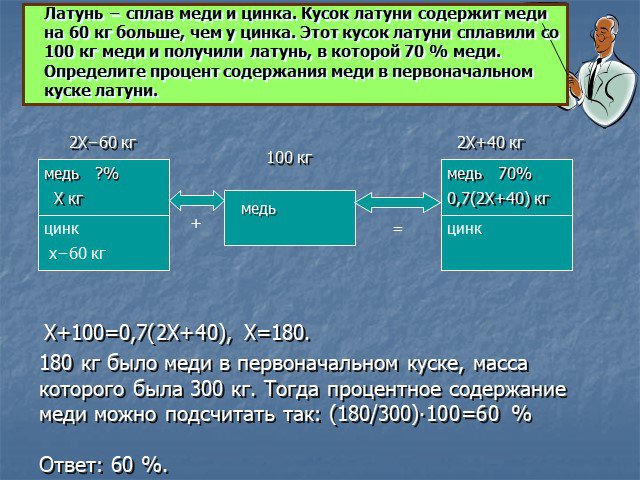
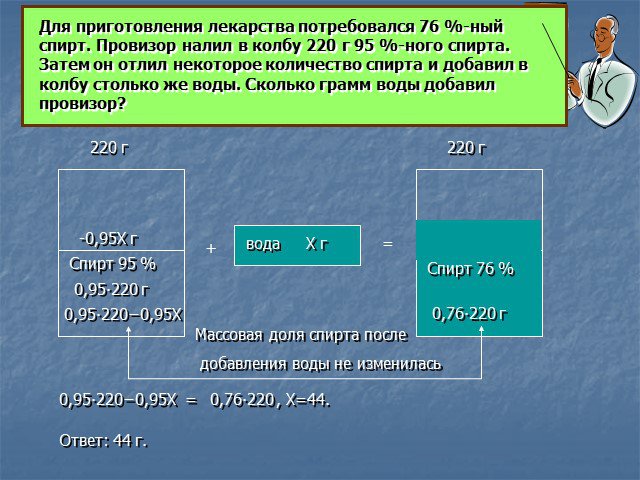
Задачи на смеси и сплавы
Цель. Расширить представления о процентных вычислениях при решении задач на смеси, сплавы, растворы Показать широту применения процентных расчетов ...Задачи на определение массовой доли веществ в смесях
Цели:. Подготовка к ЕГЭ по математике и химии Отработать умение выделять часть в целом и объединять части в целое. «Истина не рождается в голове одного ...Задачи на электролиз.
Задача 1. Водный раствор гидроксида натрия подвергли электролизу (сила тока 10 ампер, время электролиза 1 час). Определите количество веществ, выделившихся ...«Вода – основа жизни на Земле».
Вода – основа жизни на Земле. Цель: используя учебный материал курсов химии, биологии, физики, географии, экологии, обобщить знания о воде, подвести ...Гипертекст как средство развития познавательной активности учащихся на уроках химии
Анонимное тестирование учащихся 8-11 классов. Выполняете ли вы домашнее задание? Читаете ли вы параграф, заданный на дом? Вы пользуетесь компьютером ...Дисперсные системы и растворы
Дисперсные системы. Дисперсия = раздробление, измельчение. Дисперсные системы состоят как минимум из двух компонентов:. 1. дисперсионной среды, которая ...Воздействие серной кислоты на углеводы
Углеводы. Углеводы – органические вещества, молекулы которых состоят из атомов углерода, водорода и кислорода, причем водород и кислород находятся ...Вредное воздействие нитратов на организм человека
Содержание. Введение Цель проекта Задачи проекта Основные источники Качество овощей и условия их выращивания Вредное воздействие нитратов на организм ..."Химическая атака на нас"
Девиз урока: «Химики – это те, кто действительно понимает мир!». Страница 1 «Здоровье человека и средства бытовой химии». Рынок продажи средств бытовой ...Вода - самое удивительное вещество на Земле
Вода – самое распространенное и самое удивительное вещество на Земле. Вода окружает нас повсюду: в водоемах, на земле и даже в воздухе – в виде снега, ...Влияет - ли рН воды на рост бобовых
Актуальность выбора темы: Для роста растений необходимы определенные условия. Им нужен грунт, свет, вода и воздух. С помощью нашей работы мы хотели ...Влияние внешних условий на рост кристаллов различных солей
Объект исследования:. насыщенные растворы медного купороса CuSO4∙5Н2О; алюмокалиевых квасцов KCl(SO4)2*12H2O. Задачи исследования:. приготовление ...Благородные металлы на службе у человека
Цель урока:. Рассмотреть и сравнить с разных точек зрения Химии и экологии; Литературы и философии; Географии и истории Самые популярные металлы окружающие ...Буферные растворы
Концентрация – масса, объём или количество вещества в определённой массе или объёме раствора. В связи с этим концентрация может быть массовой, объёмной ...Безопасность на уроке химии
Пробовать вещества на вкус, есть и пить в химическом кабинете. Осторожно направляйте к себе газ рукой. ЗАПРЕЩАЕТСЯ. . . . . ЗАПРЕЩАЮЩИЕ ЗНАКИ. Запрещается ...Аморфные сплавы
РАЗНОВИДНОСТИ НАНОМАТЕРИАЛОВ*. *Андриевский Р.А., Рагуля А.В. «Наноструктурные материалы». 1.Консолидированные наноматериалы – пленки, покрытия из ...Алгоритм решения задач с расчётами по химическим уравнениям
Задача: Определи объём воздуха, необходимый для сжигания 24 г магния, содержащего 10 % негорючих примесей. 2Mg + O2 = 2 MgO. Составь уравнение реакции: ...Алгоритм решения задач по химии
Алгоритм решения задач по химии:. Записать краткое условие задачи; *В случае необходимости произвести предварительный расчет; Перевести величины, ...Влияние железа на организм
Железо не только основа всего мира, самый главный металл окружающей нас природы, оно – основа культуры и промышленности, оно – орудие войны и мирного ...Конспекты
Решение задач на растворы
Урок №38. . . Тема урока:. Решение задач на растворы. Цели и задачи урока:. Закрепить понятие доля компонента;. . Научить делать расчеты, ...Решение задач на вычисления, связанные с участием веществ, содержащих примеси
Тема: Решение задач на вычисления, связанные с участием веществ,. содержащих примеси. Цели: 1) Формировать умения решения расчетных задач на вычисления,. ...Решение задач на молярный объем и относительную плотность газов
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ШКОЛА №18. План конспект. открытого урока по химии. 8 класс. Тема урока:. . Решение задач на молярный ...Решение задач на определение выхода продукта реакции
Тема урока: Решение задач на определение выхода продукта реакции. Алгоритм решения задач. Составьте краткое условие задачи. . Составьте ...Решение задач на определение молекулярной формулы вещества
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №17» г. Брянска. Урок на тему: «Решение задач ...Решение задач на применение закона ЭДС индукции и определение энергии магнитного поля тока
Урок №39 9 класс. Тема: Решение задач на применение закона ЭДС индукции и определение энергии магнитного поля тока. Цель урока: проверить знания ...Решение расчетных задач на вывод химической формулы органического вещества
Муниципальное бюджетное общеобразовательное учреждение. «Средняя общеобразовательная школа №55» г. Брянска. Урок по теме:. «Решение ...Решение экспериментальных задач на распознавание катионов и анионов
Название работы:. Урок-практикум в 8-м классе на тему «Решение экспериментальных задач на распознавание катионов и анионов». Тема урока. Урок-практикум ...Обобщение и систематизация знаний по теме « Чистые вещества и смеси, массовая и объемная доли
Конспект урока по теме «Обобщение и систематизация знаний по теме « Чистые вещества и смеси, массовая и объемная доли»». Цель урока:. . 1) Обобщить ...Решение расчетных задач с валеологическим содержанием
Тема урока:. «Решение расчетных задач с валеологическим содержанием» (2 урока). Цели урока:. продолжить знакомство учащихся со способами решения ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:15 января 2015
Категория:Химия
Содержит:9 слайд(ов)
Поделись с друзьями:
Скачать презентацию