Конспект урока «Степенная функция» по математике
Методическая разработка учебного занятия
Учебная дисциплина: математика Специальность: техническая эксплуатация и обслуживание электрического и электромеханического оборудования( по отраслям ) Курс: 1 Группа:64-СЭ
Ф.И.О. преподавателя : Семеусова Ольга Ивановна
Тема занятия :Степенная функция
Тип занятия: комбинированный
Требования ФГОС СПО к уровню подготовки студентов:
Студент должен уметь:
-
определять основные свойства степенных функций, иллюстрировать их на графиках;
-
строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;
-
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Цели занятия:
Обучающая:
-
рассмотреть графики степенных функций;
-
способствовать выработке и овладению навыков строить графики с помощью преобразований;
-
повторить свойства степенных функций.
Воспитательная:
-
продолжить развитие интереса к предмету через использование необычных заданий в интерактивном режиме, инструментов интерактивной доски;
Развивающая:
-
продолжить развитие абстрактного, алгоритмического, логического мышления, произвольного внимания, кратковременной и долговременной памяти, воображения на основе решения заданий в интерактивном режиме.
-
продолжить формирование точности и аккуратности при выполнении чертежей
Междисциплинарные связи: техническая механика, геометрия.
Внутридисциплинарные связи: Тема 4 Функции, их свойства и графики, степенные, показательные, логарифмические и тригонометрические функции.
Учебное оборудование (оснащение) занятия: мультимедийный проектор компьютер, интерактивная доска
Методическое обеспечение занятия: учебники, раздаточный материал, опорные конспекты, тест №1, задания для самостоятельной работы
Опережающие задания
студентам: повторить построение графиков элементарных функций (степенных, логарифмических, показательных, тригонометрических) и их основные свойства.
Критерии и методы диагностики уровня готовности студентов к занятию (обученности):
Технологическая карта занятия
| Время | Содержание деятельности преподавателя и студентов | Методы и приемы обучения Средства обучения Формы и методы контроля качества обучения | |
| 1.Организационный этап | 5 мин. | 1.1Приветствие 1.2 Проверка по журналу явки учащихся, определение соответствия внешнего вида, готовность к уроку 1.3 Подведение студентов к постановке цели урока | Фронтальный метод организации студентов на уроке и Информационно-развивающий метод обучения |
| 2. Основной этап | 80 мин. | | |
| | | 2.1 Актуализация опорных знаний : Учитель предлагает вспомнить материал прошлых уроков, в ходе заполнения фронтального опроса и заполнения опорного конспекта. | Заполнить опорный конспект Взаимопроверка Индивидуальная работа, работа в парах Фронтальный опрос студентов Приложение 1 |
| | | 2.2 Задание « Найди ошибку» На доске высвечиваются примеры с ошибками Студенты отвечают на вопросы, слушают, аргументируют | Организационные формы работы: фронтальная, работа у доски. Активные методы обучения Презентация Приложение 2 |
| | | 2.3 « Графическое лото» | Индивидуальная работа взаимопроверка |
| | | 2.4 закрепление изученного материала в ходе Решение упражнений из учебника. | Активные методы обучения Игра-лото Самостоятельная работа и самопроверка. Приложение 3 |
| | | 2.5 практическая работа «Преобразование графиков функций» | Самостоятельное изучение материала Приложение 4 |
| 3. Заключительный этап | 5 мин. | 3.1 Подведение итогов урока Обсуждение трудных моментов. Выставление оценок | Фронтальный метод организации работы. |
| | | 3.2 Домашнее задание | Практическая работа |
| | | | |
Домашнее задание: доделать практическую работу ,
Литература:
-
Ш.А.Алимов, Ю.М.Колягин и др. «Алгебра и начала анализа 10-11»: М. «Просвещение» 2010.
-
fsm-portal.net›video…ekspress…ekzamenu-matematika…
-
http://www.1september.ru
Приложение 1. 
Опорный конспект Степенная функция у = хр
П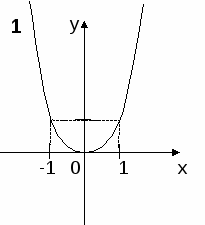
оказатель р = 2n четное натуральное число
--------------------------------------------------------------------------------
Примеры функций:
--------------------------------------------------------------------------------
Свойства функции:
--------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
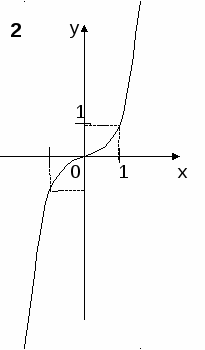Показатель р = 2n-1 нечетное натуральное число
-------------------------------------------------------------------------------
Примеры функций:
------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Показатель р = – 2n, где n – натуральное число
------------------------------------------------------------------------------
Примеры функций:
------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
--------------------------------------------------------------------------------
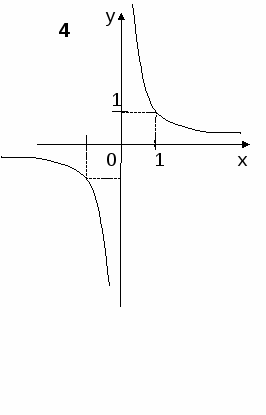
Показатель р = – (2n-1), где n – натуральное число
--------------------------------------------------------------------------------
Примеры функций:
--------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
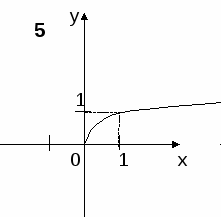Показатель р – положительное действительное нецелое число
- -----------------------------------------------------------------------------
0 p
------------------------------------------------------------------------------
Примеры функций:
------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
p > 1
------------------------------------------------------------------------------
Примеры функций:
------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Показатель p – отрицательное действительное нецелое число
------------------------------------------------------------------------------
Примеры функций:
------------------------------------------------------------------------------
Свойства функции:
------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
-
Вопрос учителя: Какая функция называется степенной?
(Функция вида 
, где p-заданное действительное число, называется степенной функцией.)
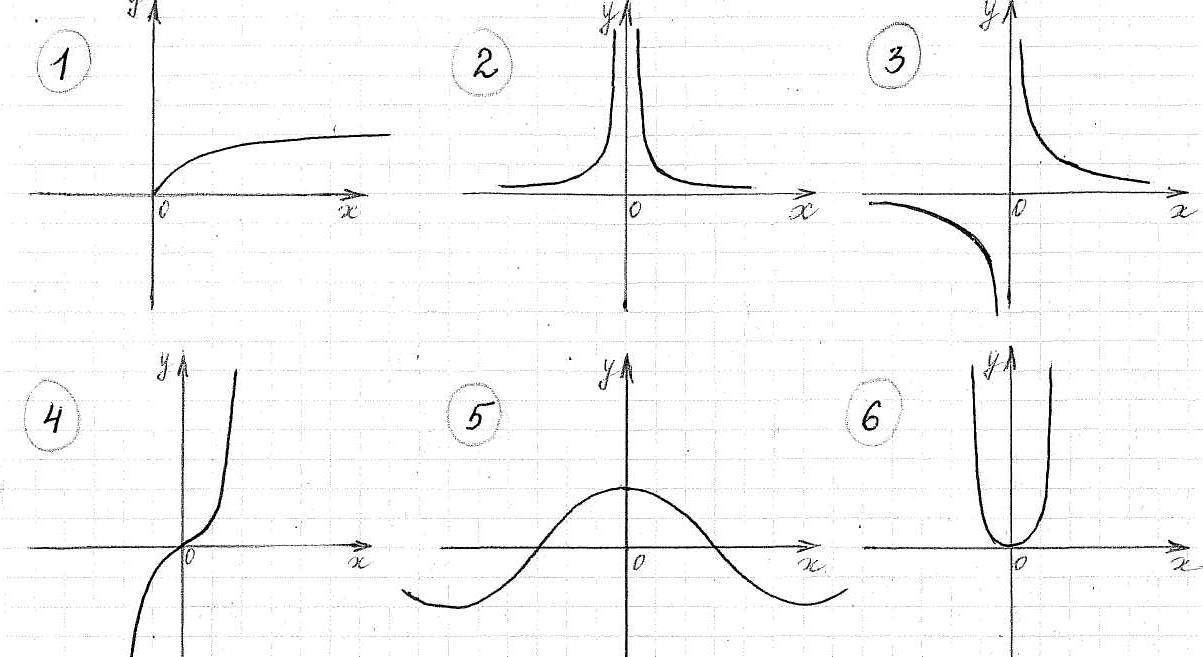
2) Даны эскизы функций. Какой график соответствует предложенной формуле. (Графики показаны на экране, формулы появляются на экране одна за другой)
Указать область определения и область значения функции.
Вопросы.
а) Какая функция «лишняя»?
б) Назовите четную функцию. Назовите нечетную функцию. Как определяем?
-
Самостоятельная работа учащихся.
Указать, какой формуле соответствует график функции: написать формулу, а рядом указать номер функции.
В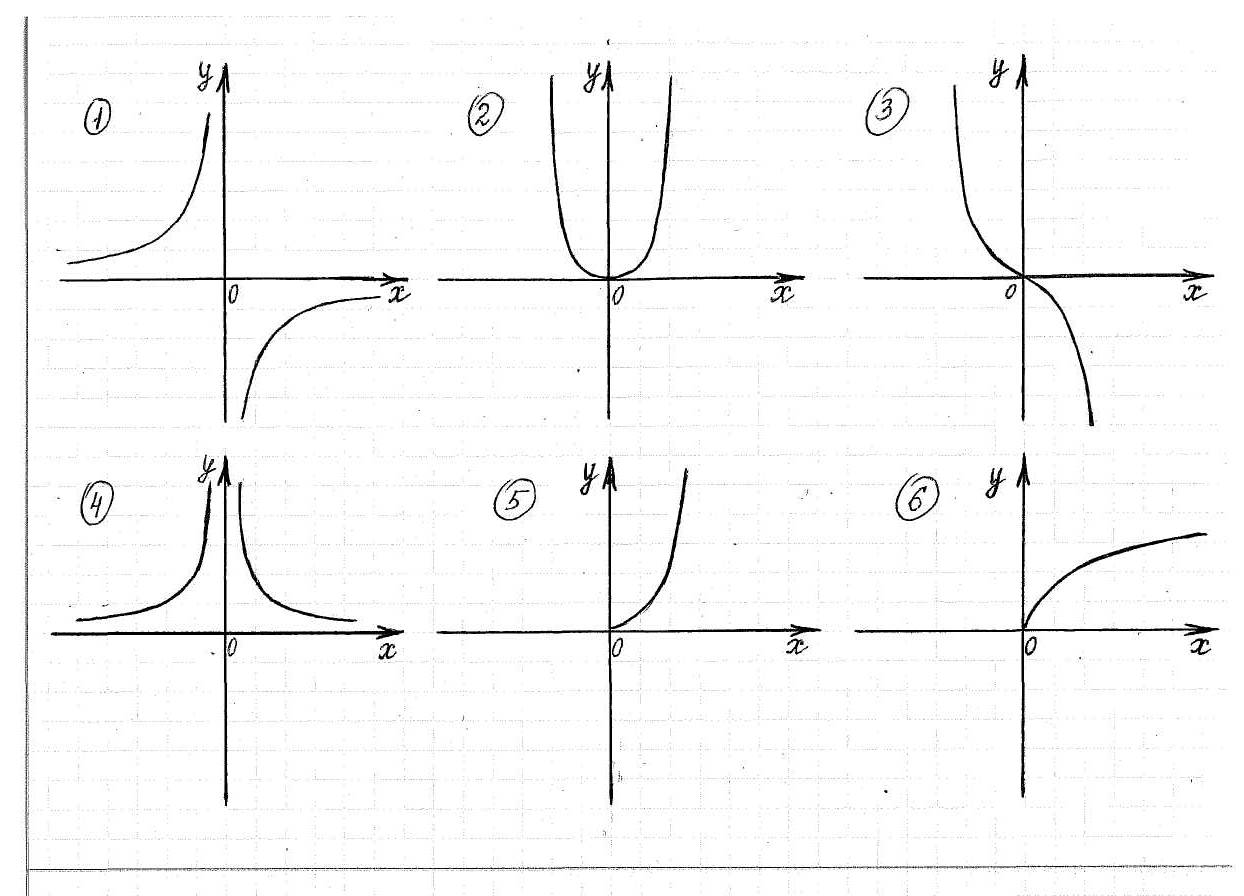
ариант 1
1)
2)
3)
4)
5)
Вариант 2
1)
2)
3)
4)
5)
Учащиеся сдают свои работы. Проверка ответов с экрана.
4) Задание учащимся: найти ошибку в решении. (На экране появляются задания по одному, учащиеся объясняют ошибки в решении. В последнем примере ошибки нет).
Найдите ошибку в решении:
-
(2a3b-2)2=2a6b-4=
-
1,2a· 5a1,5=1,2 · 5·a·a1,5=6а1,5
-
8y5:2y-4=(8:2) · (y5:y-4)=4y9
4
. Работа с учебником [1]. № 123 (2), слайд 18.
Пользуясь рисунком, найти промежутки, на которых график функции
лежит выше (ниже) графика функции у = х.
Ученику предложены два эскиза графиков (показатель р – положительное действительное нецелое число). Сначала необходимо сделать выбор эскиза графика к данной формуле функции. На одном рисунке эскиз графика функции у = хa, где a>1, а на втором рисунке эскиз графика для 0a.
Ученик у экрана работает с указкой, делает выбор.
Теперь необходимо дать полный ответ на вопросы задания.
Предлагаю ученику показать участок графика функции , который лежит выше графика функции у = х. После ответа делаю клик мышью.
Покажи и назови промежуток, на котором выполняется это условие? После ответа, делаю клик мышью.
Запись ответов на доске.
Дополнительный вопрос: почему число х = 1 не включили в ответ?
Как удалось отличить графики при выборе эскиза?
Аналогично проводится работа с заданиями №124 (2) и №127 (1), слайды 19, 20. Учителю удобно работать с дистанционной мышью во время использования презентации: он «не привязан» к компьютеру, свободно общается с классом.
5. Повторение. Построение графиков с помощью параллельного переноса вдоль координатных осей. Магнитная доска.
Чтобы светящийся экран не отвлекал учеников от новой формы работы, щелкнуть ПКМ, выбрать команду Экран – Черный экран.
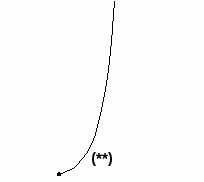
На доске расположены ветви нескольких графиков, изготовленные из картона (парабола у=х2, кубическая парабола у=х3, ветви у=х0,5 и у=х– 1,2, прямая) и записаны функции.
(
1) 
; (2) 
; (3) 
; (3) 
Какую ветвь графика можно использовать, чтобы построить все эти графики?
Выбрали ветвь (*), разворачиваем в позицию (**).
Учитель демонстрирует построение графиков на магнитной доске, используя данную ветвь, меняя позиции (*) или (**). Обучающиеся комментируют шаги построения графиков.
Дополнительные вопросы. «Чтение графика». Назвать область определения и множество значений каждой построенной функции.
Слайды 21-25. Построение графиков с помощью сдвига вдоль осей. Устная работа. Комментирование алгоритмов построения. Обратить внимание на преобразования, при которых надо выполнить также и сдвиг асимптоты графика.
6. Домашняя работа. По опорному конспекту – выучить свойства и графики.
№ 121, 123 (1) – по готовому эскизу, 124 (1) – по готовому эскизу, 127 (2), [1]. Будьте внимательны в номере 127(2) опечатка! Выполнить правильный эскиз графика к упражнению.
7. Самостоятельная работа (приложение 4).
Обучающимся выдается лист с графиками «Графическое лото» и бланк для записи ответов. В этой работе требуется вписать номер эскиза графика, который соответствует данной формуле степенной функции, т.е. привести в соответствие формулу функции и график.
Приложение 2
Графическое ЛОТО
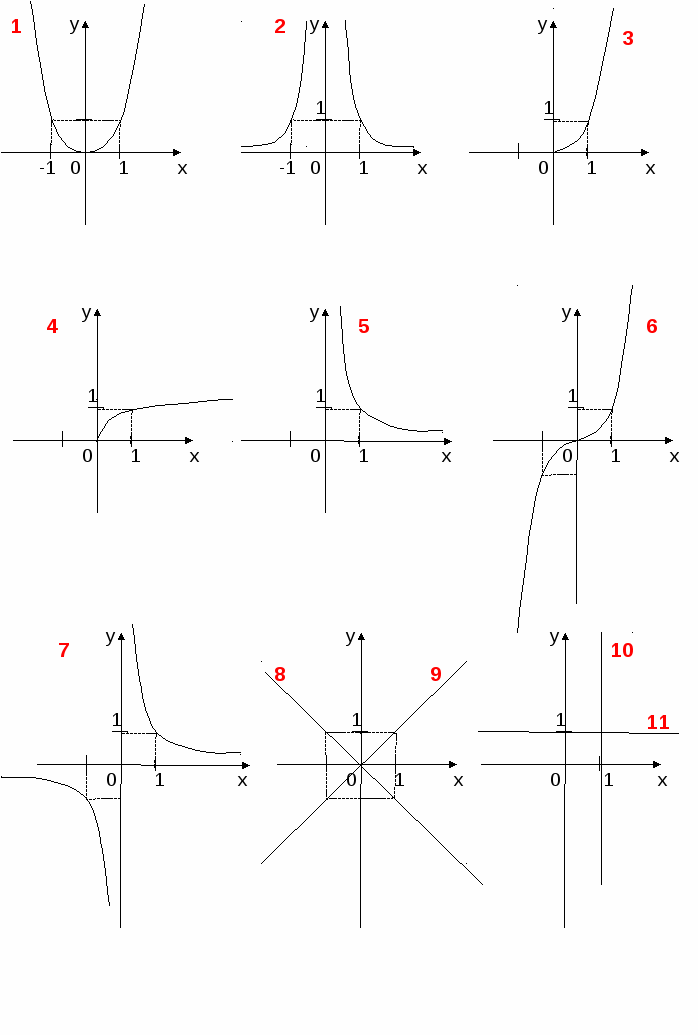
Бланки для записи ответов (два варианта).
| у = х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = –х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = х | 9 |
|
| 5 |
|
| 3 |
|
| 4 |
|
| 2 |
|
| 1 |
|
| 6 |
|
| 7 |
|
| 1 |
|
| 11 |
|
| 4 |
|
| 3 |
| у = –х | 8 |
|
| 5 |
|
| 4 |
|
| 3 |
|
| 1 |
|
| 2 |
|
| 7 |
|
| 6 |
|
| 3 |
|
| 10 |
|
| 5 |
|
| 6 |
Приложение 4
Опорный конспект по теме « Преобразование графиков функций»
| относительно оси х f(x)→- f (x) | относительно оси у f(x) →f (-x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Симметрия графика , относительно оси х Пример :у=
Замечание: точки пересечения с осью х остаются неизменными | Симметрия исходного графика относительно оси у Пример: у=
Замечание: точка пересечения графика с осью у остается неизменной | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2.Параллельный перенос вдоль оси х f(x)→ f (x-а) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| а>0 | а | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Исходный график параллельно переносим на а единиц вправо Пример: у=
| Исходный график параллельно переносим на а единиц влево Пример: у=
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.Параллельный перенос вдоль оси у f(x)→ f (x)+в | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| в>0 | в | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Исходный график параллельно переносим на в единиц вверх Пример: у=
| Исходный график параллельно переносим на в единиц вниз Пример: у=
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. Сжатие и растяжение вдоль оси х f(x)→ f (аx) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| а>1 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Исходный график сжимаем вдоль оси х в а раз Пример : у=
Замечание: точки пересечения графика с осью у остаются неизменными | Исходный график растягиваем вдоль оси х в 1/а раз Пример: у=
Замечание: точки пересечения графика с осью у остаются неизменными | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Сжатие и растяжение вдоль оси у f(x)→ кf(x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| к>1 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Исходный график растягиваем вдоль оси у в к раз Пример: у=
Замечание: точки пересечения графика с осью х остаются неизменными | Исходный график сжимаем вдоль оси у в 1/к раз Пример: у=
Замечание: точки пересечения графика с осью х остаются неизменными | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. построение графика функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y=If(x)l | y=f(lxI) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Части графика y=f(x), лежащие выше оси х, остаются без изменения, а лежащие ниже оси х- симметрично отражаются относительно этой оси (вверх) Пример: у=
Замечание: функция y=If(x)l неотрицательна, ее график расположен в верхней части полуплоскости | Части графика y=f(x), лежащие левее оси у, удаляется, а часть, лежащая правее оси у- остается без изменения и, кроме того, симметрично отражается относительно оси у(влево). Точка графика, лежащая на оси у, остается неизменной. Пример: у =
Замечание: функция y= f(lxI) четная (ее график симметричен относительно оси у). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| у = х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = –х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = –х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = –х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| у = –х | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
| 1. y = - f (x) | |
| 2. Для построения графика функции надо сохранить ту часть графика функции y = f (x), точки которой находятся на оси Ох или выше этой оси, и симметрично отразить относительно оси Ох ту часть графика функции y = f (x), которая расположена ниже оси Ох. | 2. y = f (x)+в |
| 3. График функции получается из графика функции y = f (x) симметричным отображением последнего относительно оси Ох. | 3. y = f (kx) |
| 4. График функции получается сдвигом вдоль оси Ох на величину |а| графика функции y = f (x) вправо, если а>0, и влево, если а | 4. y = f (x-a) |
| 5. График функции получается растяжением в В раз ( В >1) вдоль оси Оу графика функции y = f (x). | 5. y = |f (x)| |
| 6. Графики функции получается сжатием (при k>1) или растяжением (при kk раз вдоль оси Ох графика функции y = f (x). | 6. y = f ( -x) |
| 7. График функции получается из графика функции y = f (x) симметричным отображением последнего относительно оси Оу. | 7. y = В f (x) |
| 8. График функции получается из графика функции y = f (x) следующим образом: при х ≥ 0 график функции y = f (x) сохраняется, а при х | 8. y = f (|x|) |
Здесь представлен конспект к уроку на тему «Степенная функция», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Список похожих конспектов
Степенная функция, её свойства и график
Конспект урока по математике по теме «Степенная функция, её свойства и график». Преподаватель математики ГБПОУ МО «СТТ». Голубева Наталья Борисовна. ...
Показательная функция
Автор: учитель математики МОУ «Средняя общеобразовательная школа №41». . г.о. Саранск Тарабина Галина Михайловна. Урок – семинар по теме: « Показательная ...
Показательная функция
Урок по теме: «Показательная функция». (10 класс). Цель урока:. . обеспечить усвоение каждым учащимся знаний о показательной функции, её свойствах, ...
Показательная функция
5. . Тема урока: «Показательная функция». Класс: 11. Ельцова Наталия Ивановна,. . учитель математики. . МОУ «Александровская СОШ». ...
Логарифмическая функция, её график и свойства
Технологическая карта урока. Аттестуемый педагог: Петрова Валентина Алексеевна. . Полное название образовательного учреждения: МБОУ «Кватчинская ...
Логарифмическая функция и ее приложения
Урок математики для физико-математического профиля. . 10- 11 класса. . . Тема: «Логарифмическая функция и ее приложения». . Цели урока:. ...
Линейная функция
. Республиканский институт образования. Кафедра математики и информационных технологий. Конспект урока. по математике в 7 классе. ...
Функция. Линейная функция
Функция. Линейная функция. . . ФИО (полностью). . Кукушкина Елена Владимировна. . . . . Место работы. . ВСОШ №6. . . ...
Логарифмическая функция
«Логарифмическая функция». Учитель: Черная Марина Михайловна. Класс: 10. Ресурсы: теоретический материал учебника Алимова и дополнительная литература ...
Линейная функция и ее свойства
Кочуева Людмила Николаевна. МКОУ «Рождественская ООШ» п. Тим. Учитель математики. Разработка открытого урока по математике в 7 классе. . ...
Линейная функция и её применение
Наименование ОУ:. МБОУ СОШ №12 г. Саров. ФИО автора:. Градова Юлия Геннадьевна. Должность:. учитель математики. . Бизнес-игра «УМА ПАЛАТА». ...
Линейная функция и ее график
Яковлева Ангелина Андреевна, учитель математики. МБОУ «СОШ №19» г.Новочебоксарск. Открытый урок по теме «Линейная функция и ее график». 7-а ...
Линейная функция и ее график
МБОУ «Букреевская основная общеобразовательная школа». Курский район. Конспект открытого урока по математике (алгебра). . в 7 классе по теме ...
Показательная функция, её свойства и график
Государственное областное бюджетное. профессиональное образовательное учреждение. «ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ». Методическая разработка. ...
Логарифмическая функция
Логарифмическая функция. Цели урока:. знать определение логарифмической функции, ее основные свойства; уметь строить график логарифмической функции, ...
Логарифмическая функция и её приложения
Тема урока. «Логарифмическая функция и её приложения». Цель урока: * расширить представление учащихся о логарифмической. функции, применении ...
Что такое функция
МАРШРУТНЫЙ ЛИСТ обучения, взаимоконтроля и самоконтроля по теме:. Урок 1. . Тема. :. Что такое функция. . . ( учебник стр. 51-53). Класс 7 А. Фамилия, ...