Конспект урока «Функции и их графики» по алгебре для 9 класса
МОУ – СОШ №4
Урок алгебры в 9-а классе
« Функции и их графики»
Авторский урок
подготовила и провела
учитель математики I категории
Китаева Т.Ф.
Copyright MyCorp © 2013
27 апреля 2013 г.
- 1 –
1. Цель:
-
формирование умения определять и описывать свойства функции по графику;
-
подготовка к ГИА.
2. Задачи:
-
создать условия для воспроизведения и систематизации учащимися полученных знаний и способов действий;
-
организовать внешний контроль усвоения материала;
-
содействовать развитию навыков самоконтроля в процессе выполнения заданий.
3. Тип урока: повторительно – обобщающий.
4. Структура урока:
1 этап – мотивационный; 2 этап – актуализация знаний; 3 этап – деятельностный; 4 этап – подведение итогов; 5 этап – рефлексия
5. Применяемые педагогические технологии:
-
постановка проблемы «Разобрать и решить задания по теме», т. е. отработать основные ЗУН , которые ученик должен усвоить в процессе обучения и применить их на экзамене;
-
применение уровневой дифференциации и индивидуализации;
-
использование коллективного способа обучения – групповой деятельности.
6. Использованные методы:
-
обучающая групповая работа по дидактической направленности;
-
самостоятельное выполнение тестовых заданий.
1 этап. Организационный момент
Прежде, чем начать урок, хочу процитировать слова русского учёного Николая Жуковского: «В математике есть своя красота, как и в живописи и
- 2 -
поэзии». Очень хочу, чтобы вы почувствовали красоту в математике вообще, а в графиках, в частности.
Тема сегодняшнего занятия – « Функции и их графики». Как вы считаете, какова цель нашего урока? Наша цель: - устранить все пробелы по данной теме, - научиться распределять время, отведённое для выполнения работы, - оценить свои возможности в работе с экзаменационным материалом, - сделать для себя вывод о собственных возможностях решения экзаменационной работы.
Перед вами лежит листок рефлексии. Подпишите этот листок. За каждый верный ответ на фронтальном опросе ставите себе один плюс, за каждый правильно решённый номер теста – 1 балл. (Эти задания соответствуют заданиям 1-ой части экзаменационной работы). Задания 2-ой части дифференцированы, т. е. вы по желанию выполняете одно из предложенных заданий, которые оцениваются в 3балла и 4 балла. В конце урока подведём итоги.
2 этап. Актуализация знаний учащихся
Беседа с учащимися.
1. Дайте определение функции. Задание 1. Какие из графиков, изображённых на доске, не являются графиками функций?
2. На доске – графики известных вам функций. Какой функции соответствует каждый из графиков?
3. Давайте поговорим о свойствах функций. Какие свойства функций вам известны?
а) Область определения функции. Что такое область определения функции? Задание 1. Какова область определения функций: у = х2 ; у = ![]() .
.
б) Множество значений функции.
Что такое множество значений функции? Задание 2. Назовите множество значений функций: у = ![]() ; у = х2.
; у = х2.
- 3 -
в) Нули функции. Задание 3. Назовите нули функций: у = х3 ; у = ![]() .
.
г) Промежутки возрастания, убывания функции. Задание 4. Назовите промежутки возрастания и убывания функций: у = х2; у = ![]() где k > 0.
где k > 0.
д) Наибольшее и наименьшее значения функции. Задание 5. Каковы наибольшие и наименьшие значения данных функций?
4. Какова роль коэффициентов k и l в уравнении прямой y = kx + l ?
5. Какова роль коэффициентов а и с в уравнении параболы y = ax2 + bx + c?
3 этап.
Решение задания ГИА повышенной сложности
( у доски )
( 6 баллов ). Постройте график функции у = ![]() . Сколько общих точек может иметь с этим графиком прямая y = m ? ( Для каждого случая укажите соответствующие значения m ).
. Сколько общих точек может иметь с этим графиком прямая y = m ? ( Для каждого случая укажите соответствующие значения m ).
Решение тестовых заданий (тест 1 по вариантам самостоятельно)
6. Объясните, как с помощью графиков функций y = f1(x) и y = f2 (x)можно решить уравнение f1(x) = f2 (x).
7. Как определить решения системы двух уравнений с помощью графиков функций?
Решение тестовых заданий (тест 2 групповая работа)
Решение заданий ГИА части 2
( дифференцированная работа )
Задача . Постройте график функции ![]() . При каких значениях m прямая y = m имеет одну общую точку с графиком данной функции?
. При каких значениях m прямая y = m имеет одну общую точку с графиком данной функции?
4 этап. Подведение итогов.
- 4-
Проверка ответов тестовых заданий (тест 1 и тест 2).
5 этап. Рефлексия
Подведение итогов. Выставление оценок за урок.
- 5 -
Тест 1 1 в а р и а н т
-
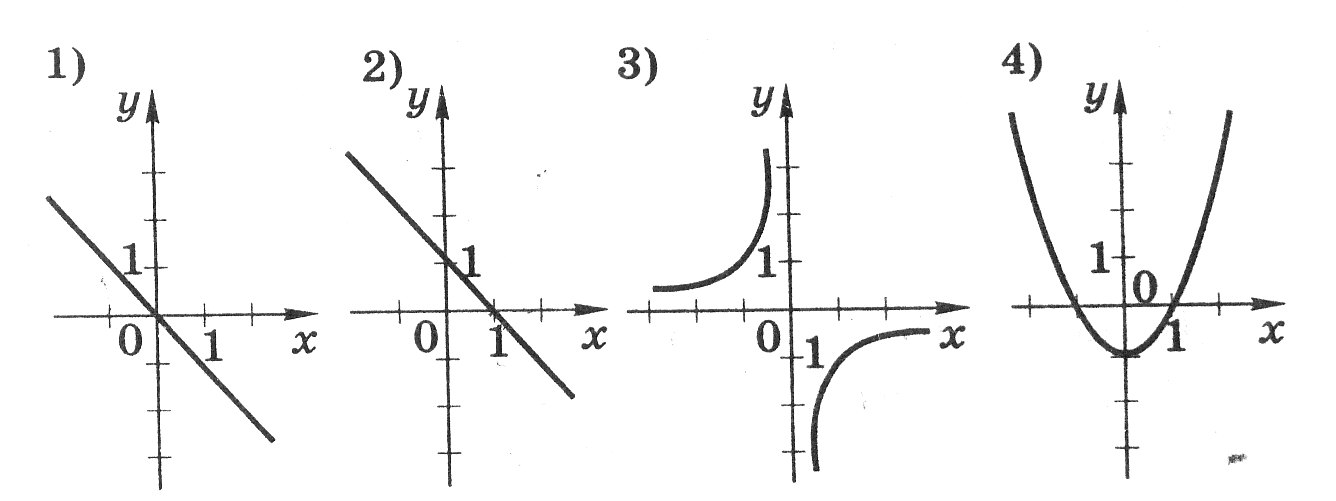
Каждый график соотнесите с соответствующей ему формулой.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
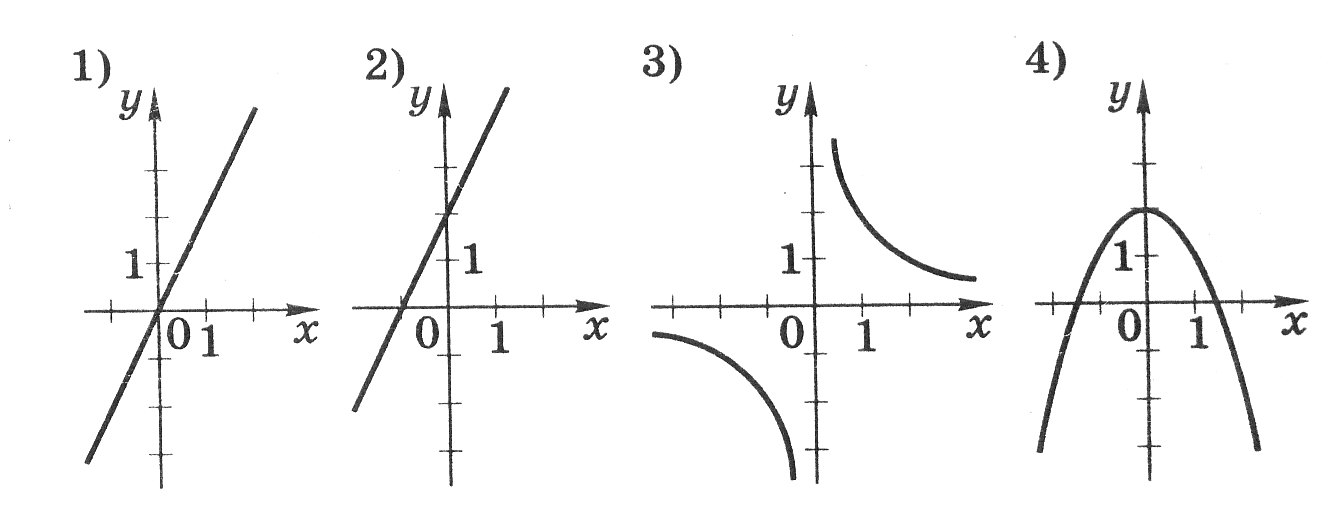
-
а
б
в
г
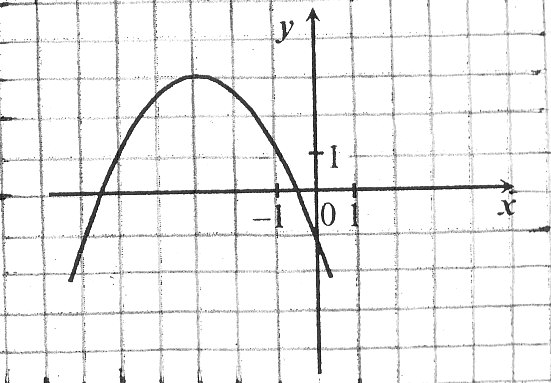
2. По данному графику квадратичной функции ![]() определите проме – жуток, в котором функция возрастает.
определите проме – жуток, в котором функция возрастает.
1) (-![]() 2) (-3; +
2) (-3; +![]()
3) (-![]()
3. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками и знаками коэффициентов k и b.
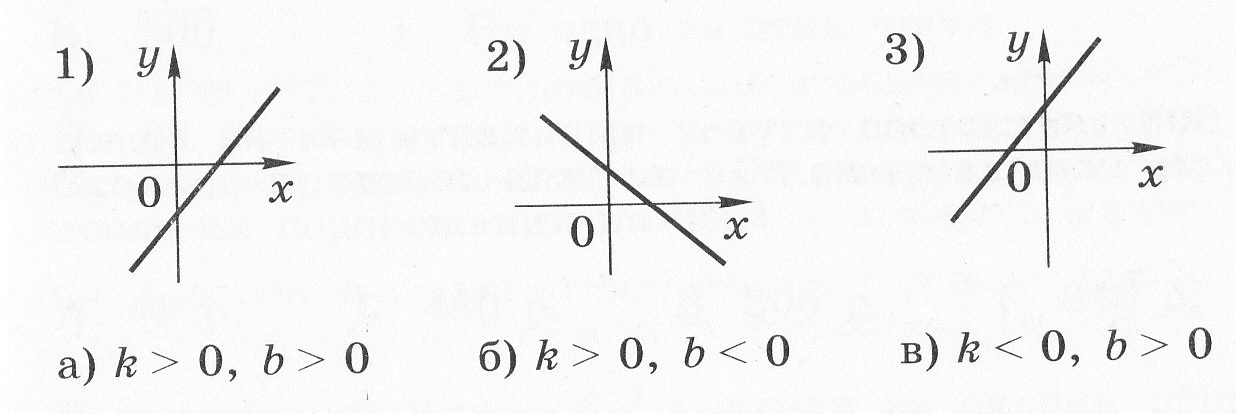
-
1
2
3
- 6 -
4. График какой квадратичной функции изображён на рисунке?
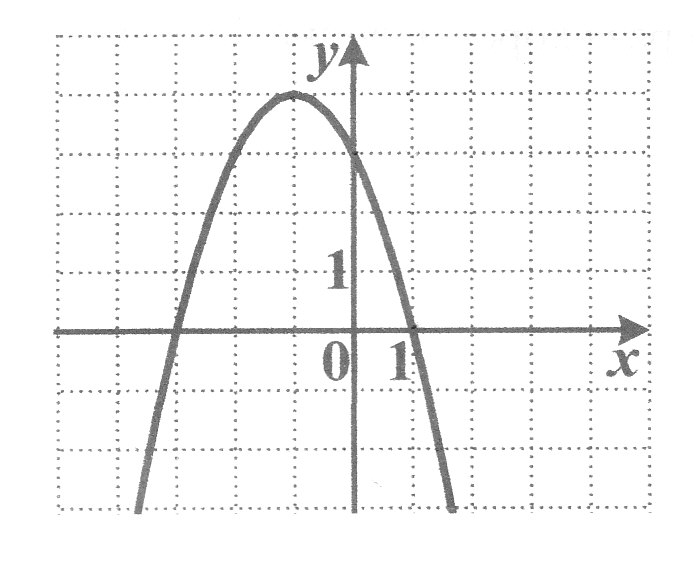 1) у = - х2 + 2х + 3 2) y = x2 +2x + 3
1) у = - х2 + 2х + 3 2) y = x2 +2x + 3
3) у = х2 – 2х + 3 4) у = - х2 – 2х + 3
5. Для какой из линейных функций нет соответствующего графика?
А. ![]() Г.
Г. ![]()
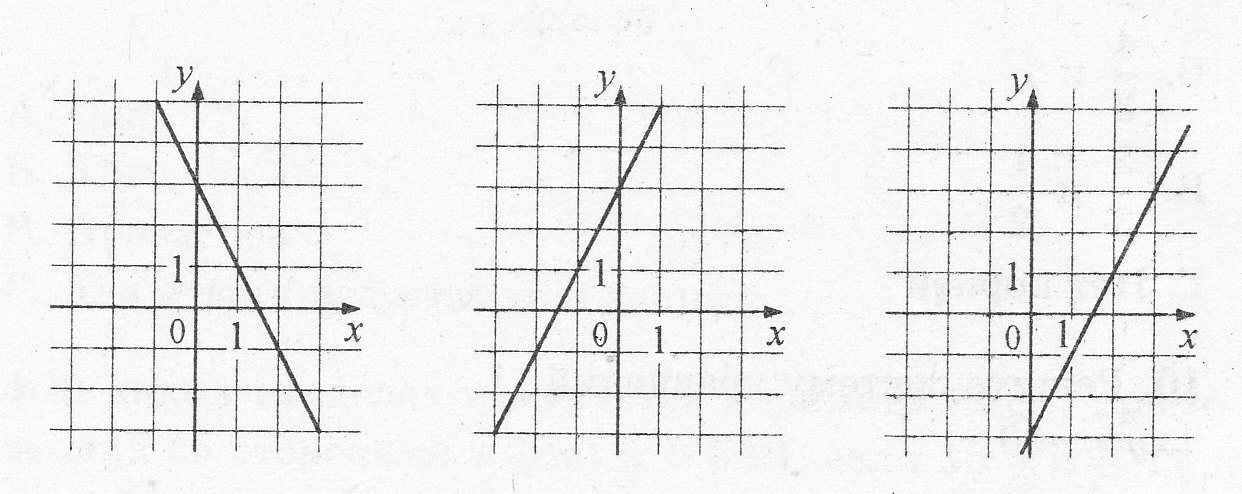
6. График какой функции изображён на чертеже?
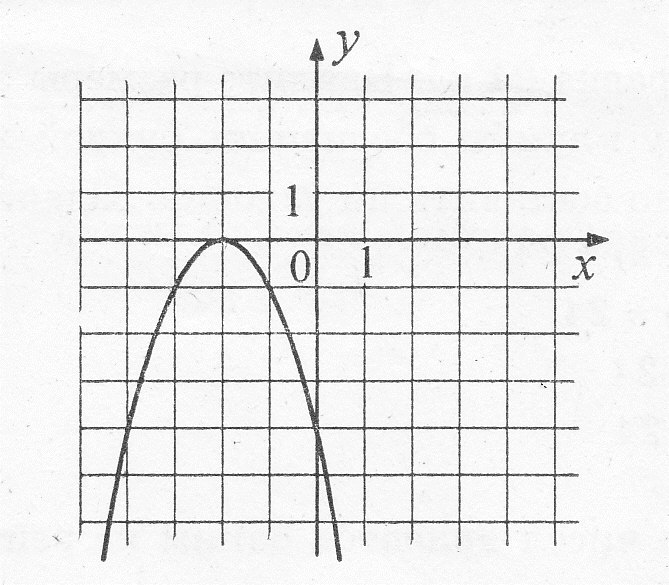 1) у = (х + 2)2
1) у = (х + 2)2
2) у = - х2 – 2
3) у = - (х + 2)2
4) у = - (х - 2)2
- 7 –
Тест 1 2 в а р и а н т
-
Каждый график соотнесите с соответствующей ему формулой.
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
-
а
б
в
г
-
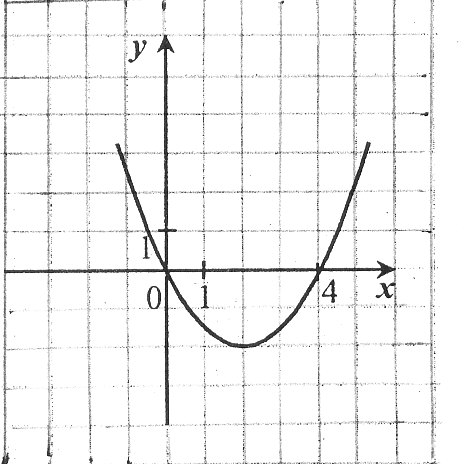
По данному графику квадратичной функции
 определите проме – жуток, в котором функция убывает.
определите проме – жуток, в котором функция убывает.
1) (-![]() 2) (2; +
2) (2; +![]() 3) (-
3) (-![]()
3. На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками и знаками коэффициентов k и b.
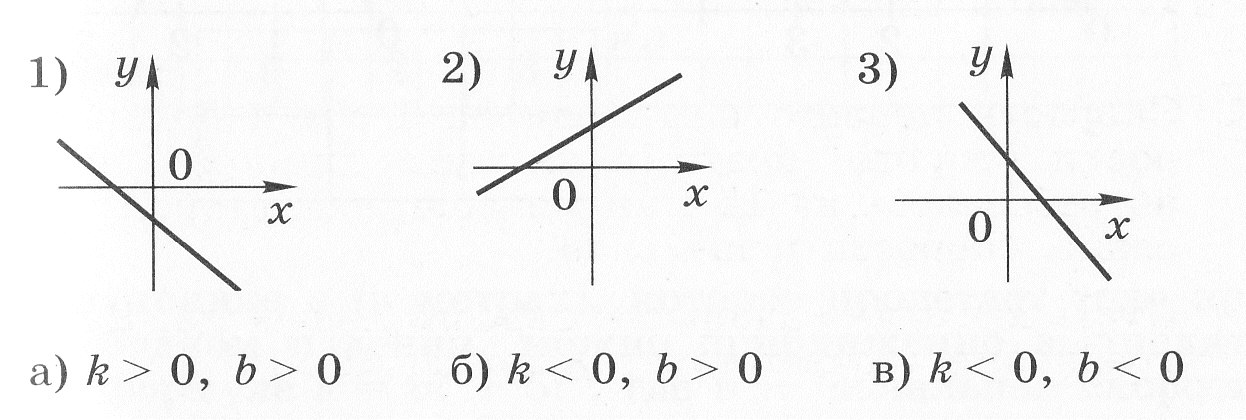
-
1
2
3
- 8 -
4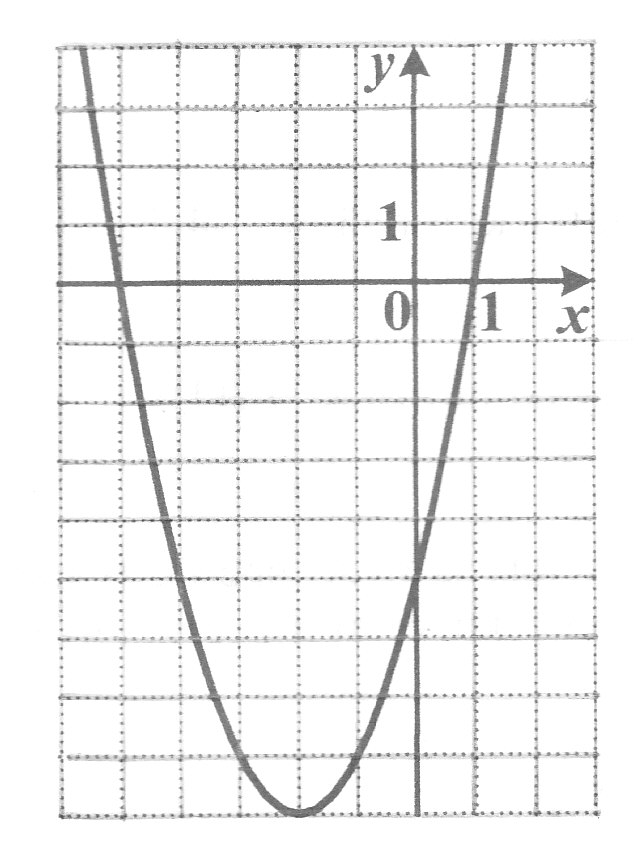 . График какой квадратичной функции изображён на рисунке?
. График какой квадратичной функции изображён на рисунке?
1) у = - х2 - 4х - 5 2) y = - x2 +4x - 5
3) у = х2 + 4х - 5 4) у = х2 – 4х - 5
5. Соотнесите уравнение прямой с графиком этой прямой:
А. ![]() Г.
Г. ![]()
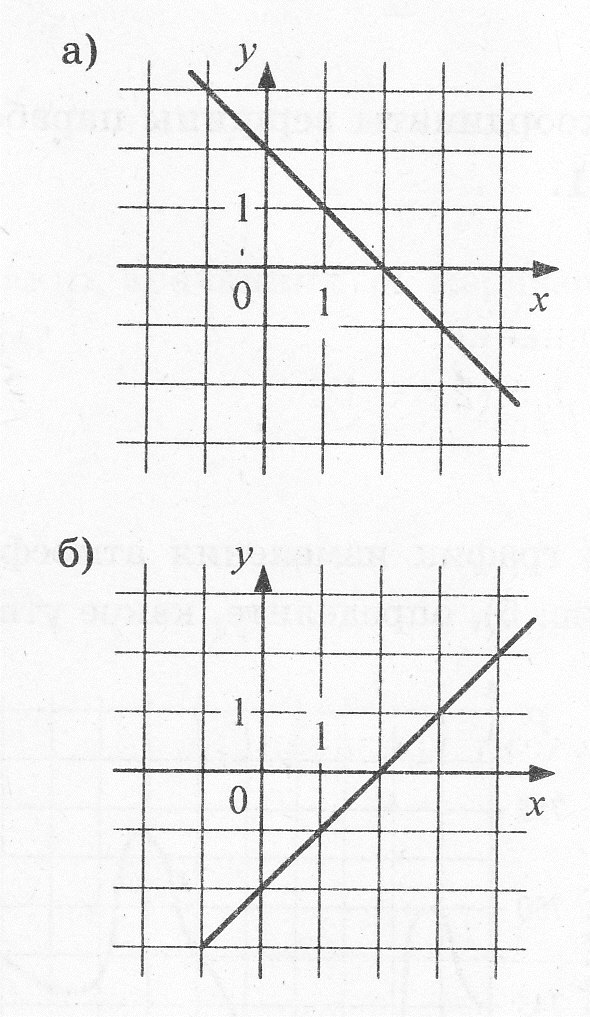
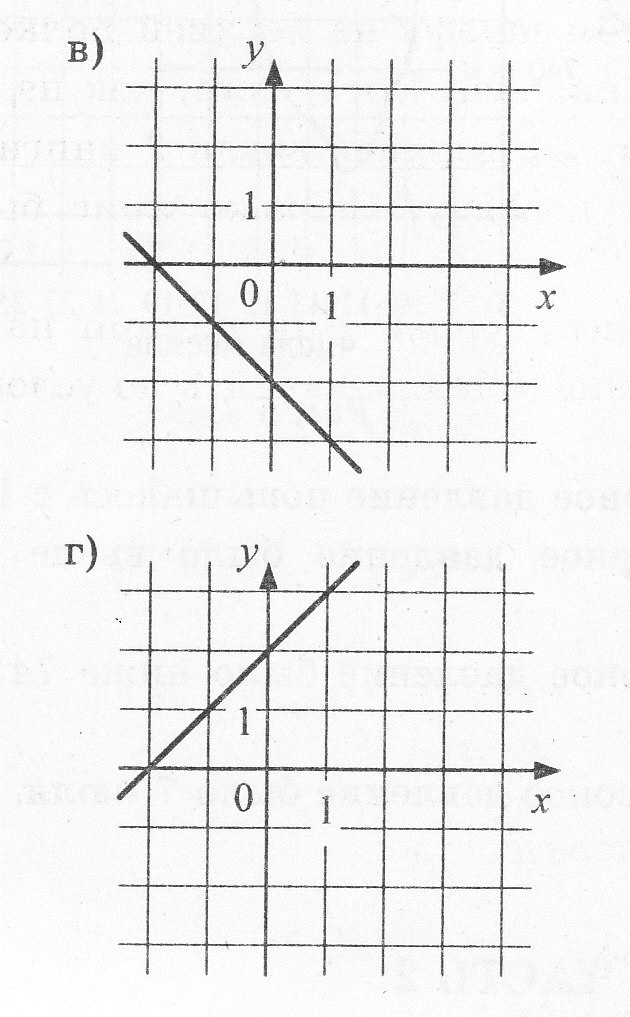
-
А
Б
В
Г
6. Какой формулой задаётся функция, график которой изображён на чертеже?
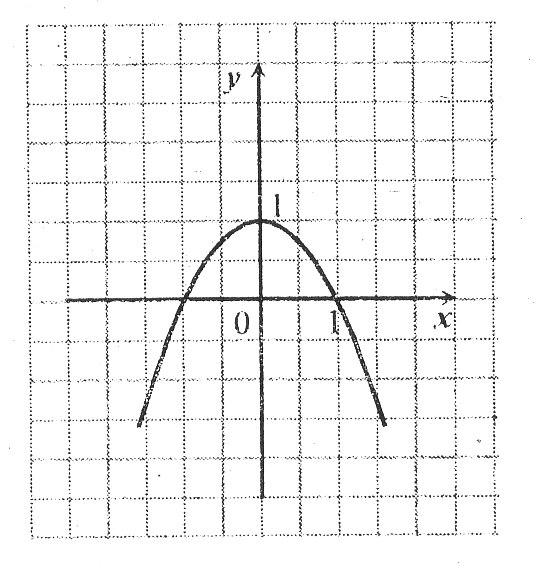 1) у = х2 + 1
1) у = х2 + 1
2) у = (х + 1)2
3) у = - х2 + 1
4) у = - х2
- 9 -
Тест 2 1 в а р и а н т
-
Используя графики функций у = х3 и у = - х + 2, решите уравнение х3 + х – 2 = 0.
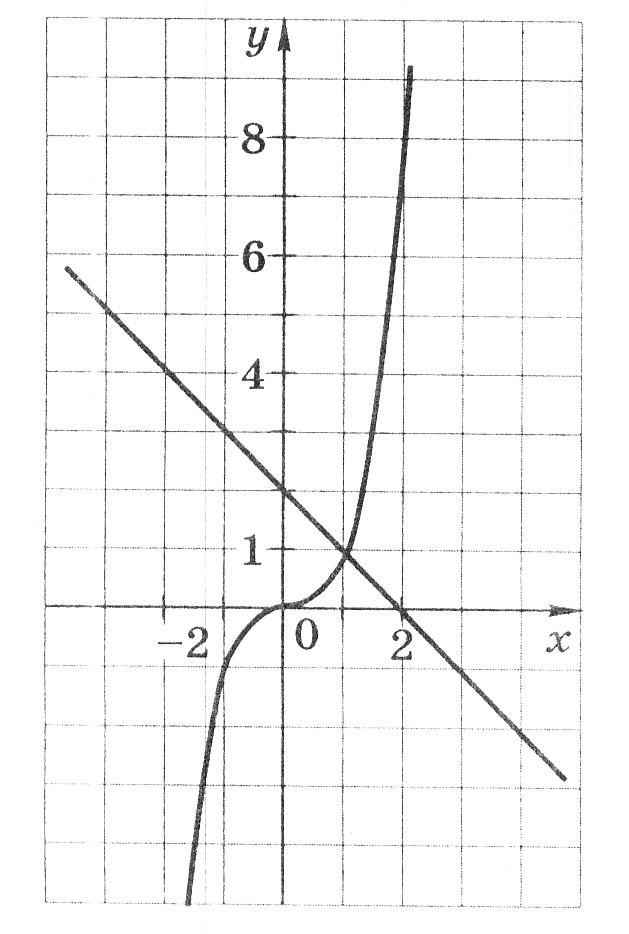 Ответ:________
Ответ:________
-
Используя графические представления, для каждой системы уравнений укажите соответствующее ей утверждение.
А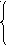
 ) y = -
) y = - ![]() , Б) у =
, Б) у = ![]() , В) у = - х,
, В) у = - х,
y = - x. y = - x. у = х2.
-
Система имеет одно решение.
-
Система имеет два решения.
-
Система не имеет решений.
| Б | В | |
| | | |
-
На рисунке изображён график функции у = х2 + 2х. Используя этот график, решите неравенство х2 + 2х
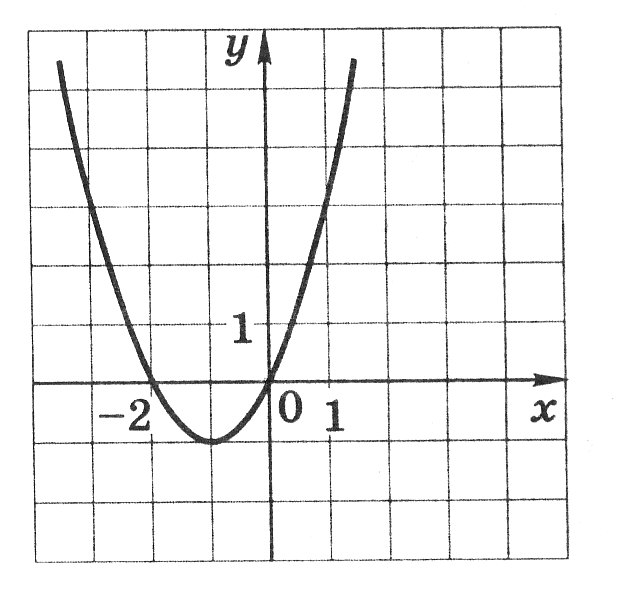 Ответ:_________
Ответ:_________
- 10 -
-
Три прямые заданы уравнениями: А)
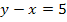 , Б)
, Б) 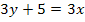 , В)
, В) 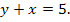 Какие из этих прямых параллельны?
Какие из этих прямых параллельны?
1) А и Б; 2) Б и В; 3) А и В; 4) среди этих прямых параллельных нет
-
Для каждой системы уравнений укажите число её решений. (Для ответа используйте графики; график уравнения
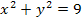 изображён на рисунке.)
изображён на рисунке.)
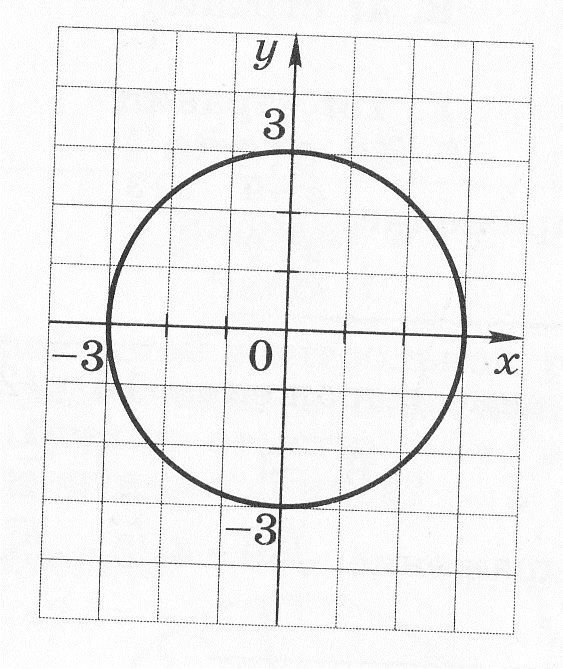
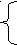
-
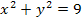 ,
,
![]() + 4.
+ 4.
-
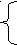
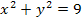 ,
,
![]() - 3.
- 3.
-
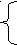
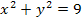 ,
,
![]() + 2.
+ 2.
а) Нет решений б) Два решения в) Три решения
Ответ:
-
1
2
3
- 11 -
Тест 2 2 в а р и а н т
-
Используя графики функций у = х3 и у = 2х + 4, решите уравнение х3 - 2х – 4 = 0.
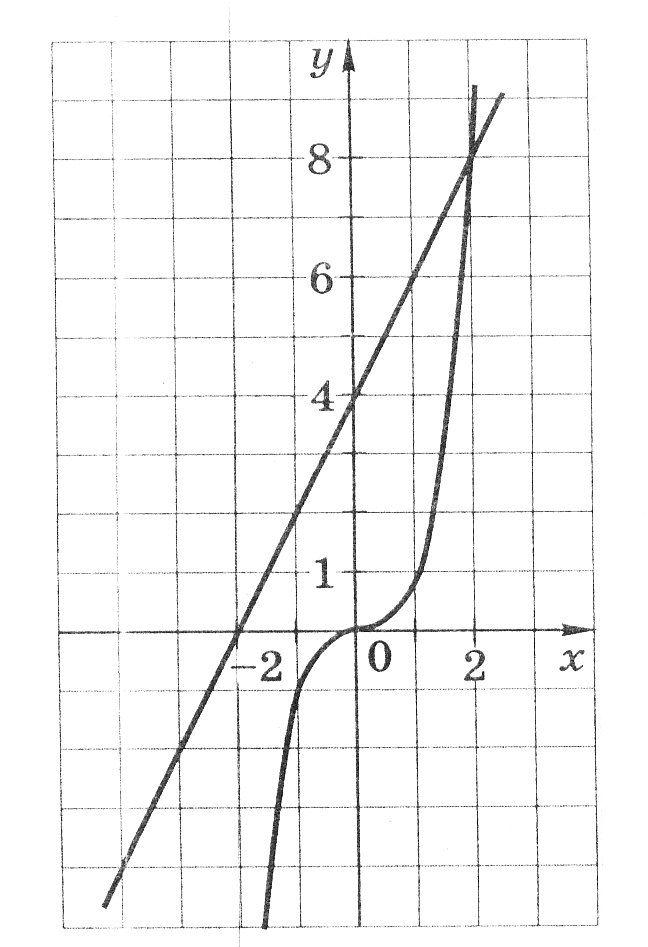
Ответ:_________
-
Используя графические представления, для каждой системы уравнений укажите
соответствующее ей утверждение.
А
 ) y =
) y = ![]() , Б) у =
, Б) у = ![]() , В) у =
, В) у = ![]() ,
,
y = x. y = - x. у = х2.
-
Система имеет одно решение.
-
Система имеет два решения.
-
Система не имеет решений.
| Б | В | |
| | | |
-
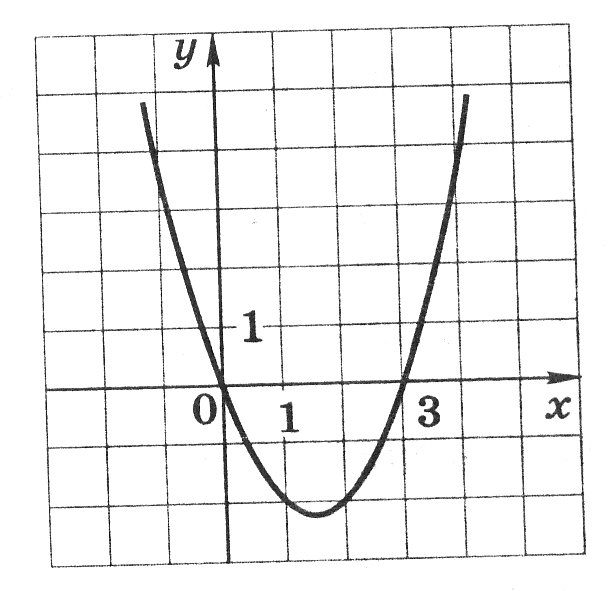
На рисунке изображён график функции у = х2 – 3х. Используя этот график, решите неравенство х2 – 3х
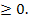
 Ответ: ____________
Ответ: ____________
- 12 -
-
Определите расположение на плоскости графиков линейных функций
![]() и
и ![]()
-
пересекаются; 2) параллельны друг другу; 3) совпадают;
-
параллельны оси абсцисс.
-
Для каждой системы уравнений укажите число её решений. (Для ответа используйте графики; график уравнения
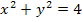 изображён на рисунке.)
изображён на рисунке.)
-
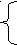
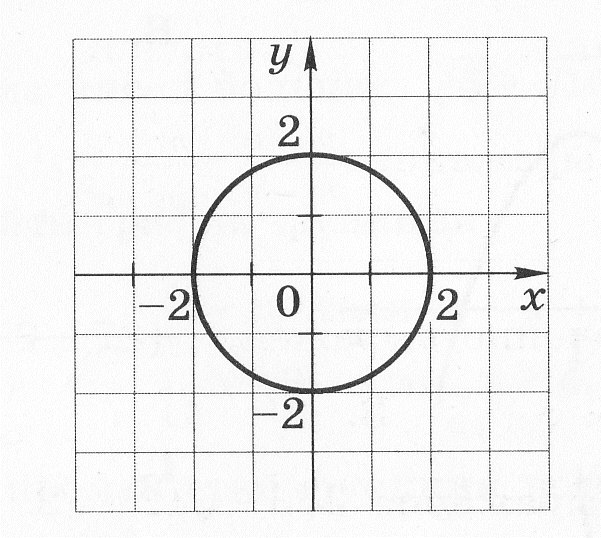
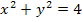 ,
,
![]()
![]()
![]() ,
,
![]() + 2
+ 2
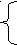
3) ![]() ,
,
![]() + 3.
+ 3.
а) Нет решений б) Одно решение в) Два решения
Ответ:
-
1
2
3
- 13 -
Листок рефлексии
За каждый верный ответ на фронтальном опросе – один «плюс». За каждый правильно решённый номер теста – 1 балл.
-
менее 6 баллов - «2»
-
6 – 10 баллов - «3»
-
11 – 14 баллов - «4»
-
15 – 17 баллов - «5»
-
Фронтальный
опрос
Тест 1
№1
№2
№3
№4
№5
№6
Тест 2
№1
№2
№3
№4
№5
Задание ч.2
Итого (баллов):
Оценка
Здесь представлен конспект к уроку на тему «Функции и их графики», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Алгебра (9 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.

