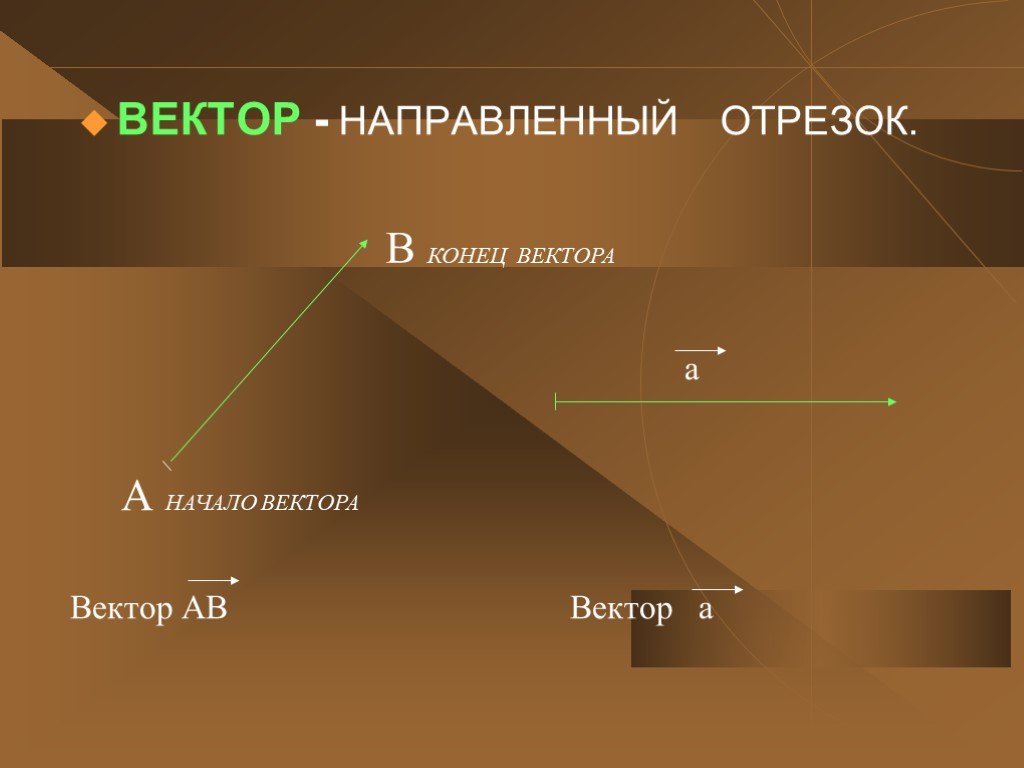
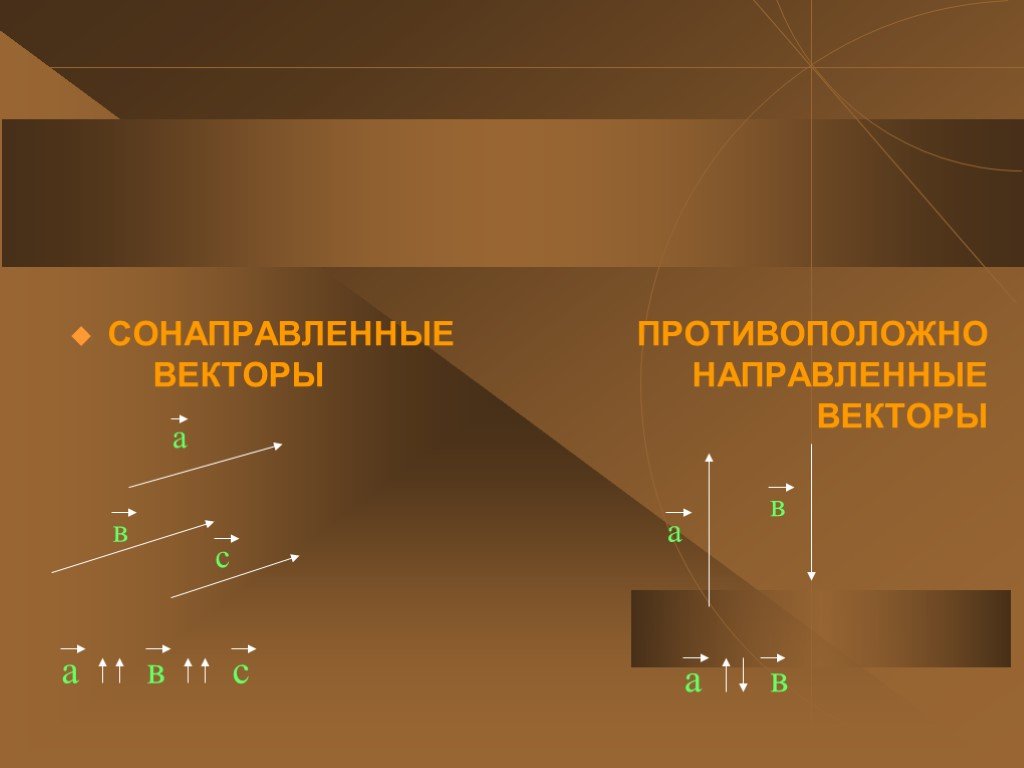
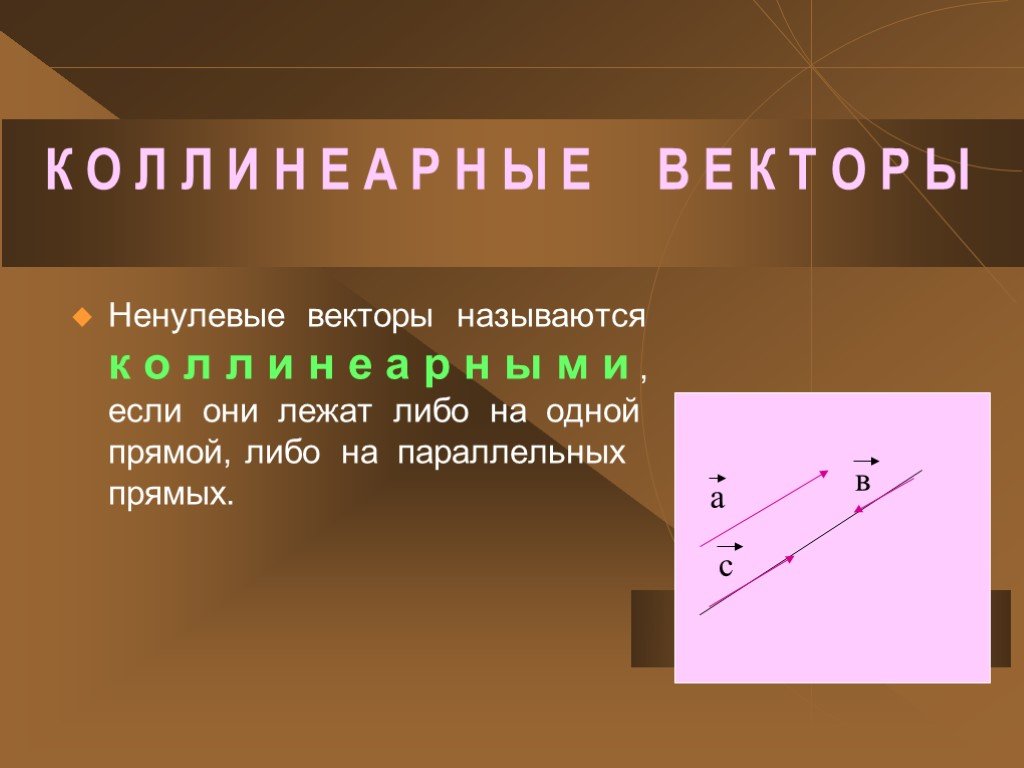
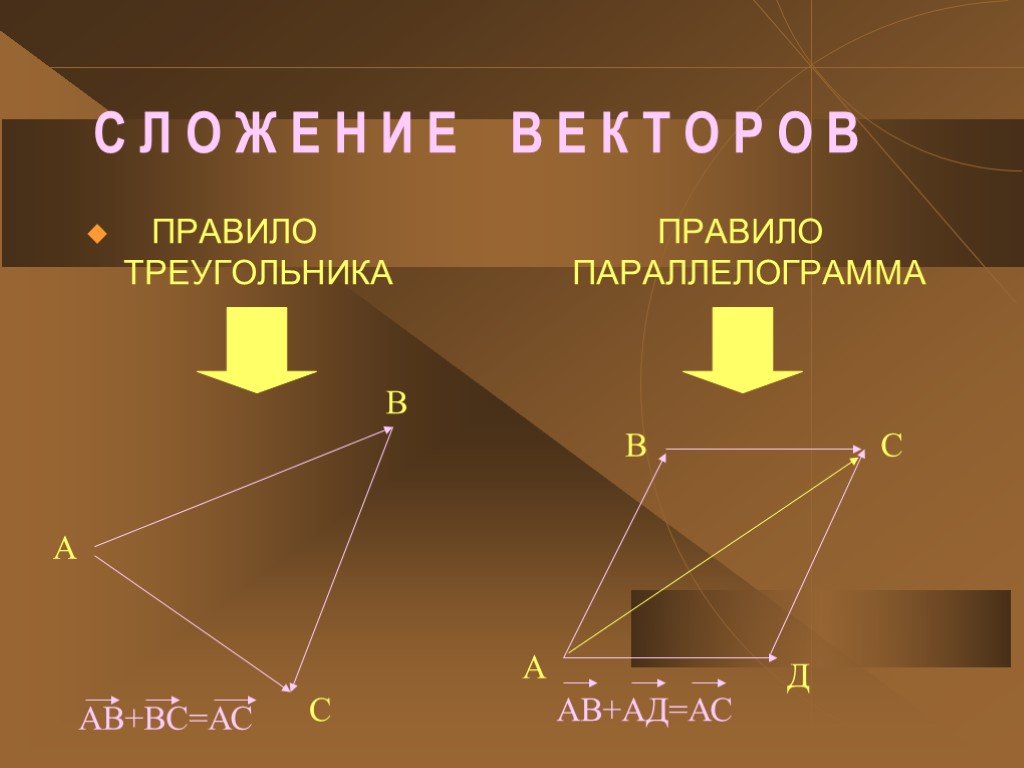
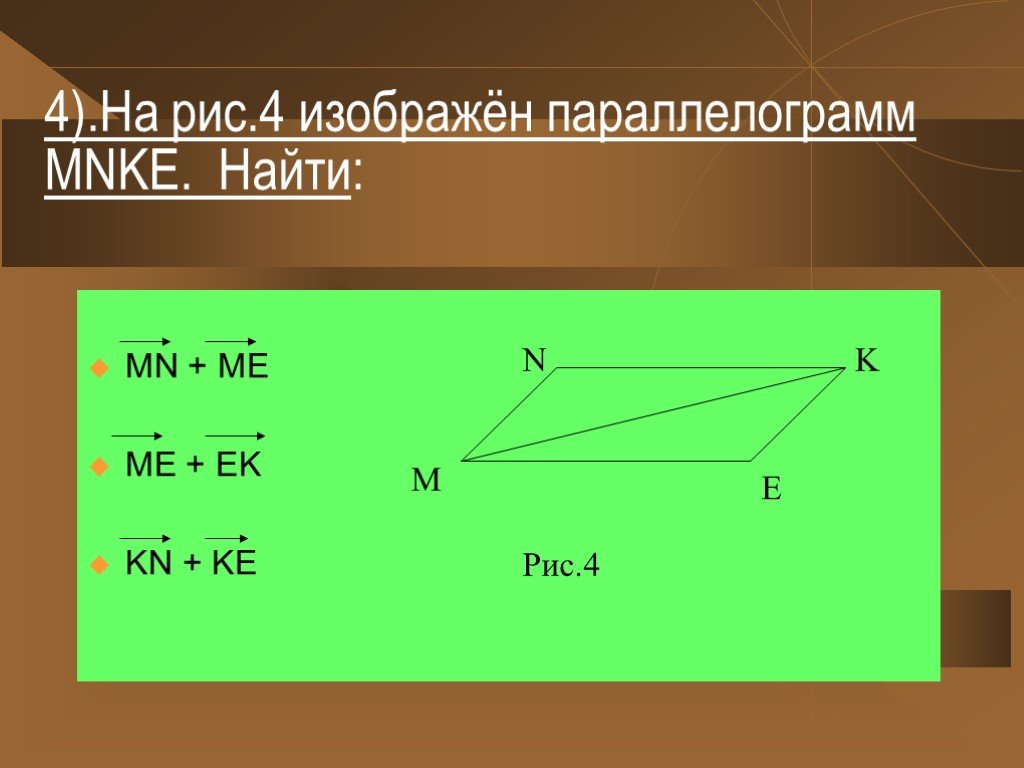
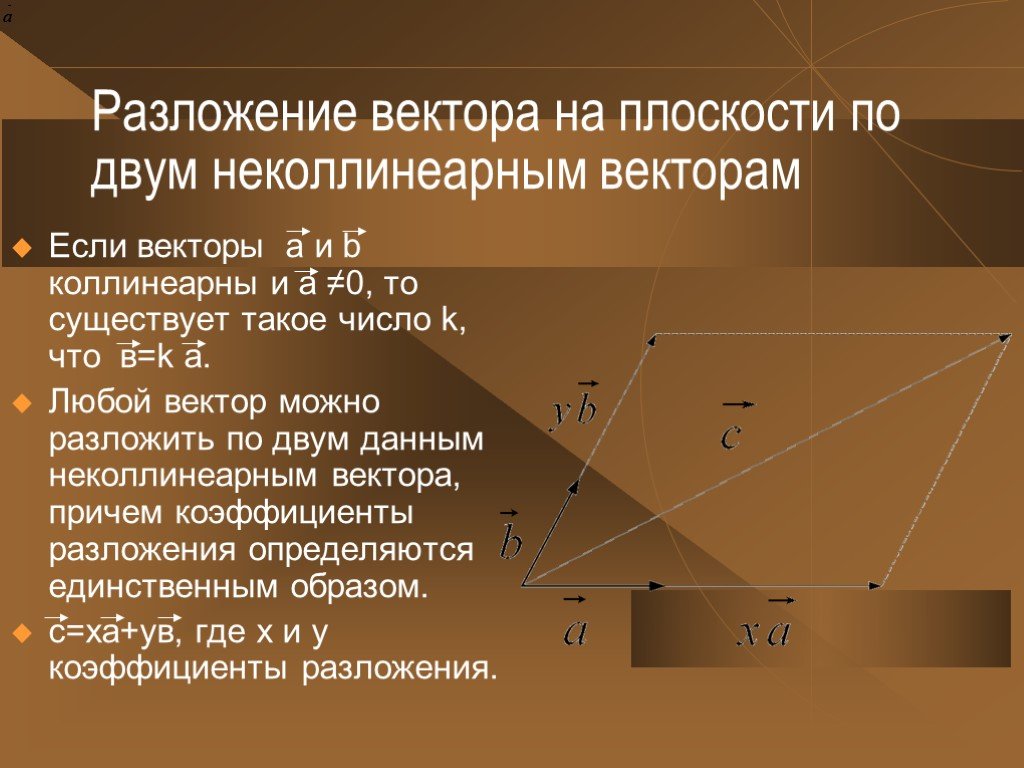
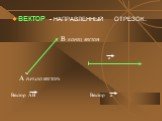
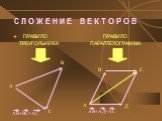
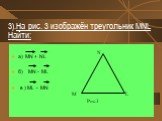
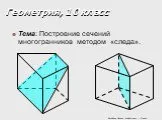
Презентация "Геометрия «Векторы»" (9 класс) – проект, доклад
Презентацию на тему "Геометрия «Векторы»" (9 класс) можно скачать абсолютно бесплатно на нашем сайте. Предмет проекта: Математика. Красочные слайды и иллюстрации помогут вам заинтересовать своих одноклассников или аудиторию. Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад - нажмите на соответствующий текст под плеером. Презентация содержит 21 слайд(ов).
Слайды презентации
Список похожих презентаций
Геометрия Лобачевского
Проблема V постулата. Система аксиом современных школьных учебников геометрии базируется на системе аксиом Евклида. Евклидова геометрия на протяжении ...Геометрия объёмы
Условие:. Дан каток, который требуется залить n количеством воды, находящейся в цистерне, где радиус цистерны 1м, высота 6м. Площадь ледового покрытия ...Геометрия и построение выкроек одежды
Содержание:. Виды мужских фигур. Виды женских фигур. Геометрия в моделировании и создании выкроек: снятие мерок; конструирование; построение выкроек ...Геометрия крыла
Цель проекта. Исследовать разные формы крыльев, разных летательных аппаратов; Бионику геометрии крыла; Провести эксперимент по проверке эффективности ...Страна "Геометрия"
Темнеет.... Бабушка-математик стала рассказывать сказку детям о стране Геометрии. В этой стране жили странные существа такие как: Теоремы, треугольники ...Геометрия и архитектура
Цель работы:. Показать возможности Геометрии в архитектуре. Наука Геометрия. Геометрия - одна из древнейших частей математики, изучающая пространственные ...Геометрия «Аксиома параллельных прямых»
«Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». (В. Произволов). ...ГИА 2013. Модуль Геометрия №13
Повторение(3) Ответ: 23. Укажите номера верных утверждений. 1.Через любые три различные точки плоскости можно провести единственную прямую. 2.Если ...Геометрия
Учёные, внесшие вклад в развитие геометрии. Фалес Древнегреческий философ и математик, астроном и физик, путешественник и торговец, а также военный ...Геометрия
1. Построить A. 2. Построить окружность произвольного радиуса с центром в вершине A. . . 4. Построить две окружности равного радиуса с центрами ...Геометрия
178' 179' 180' 181'. Задача №1 А В С а 1 2 Дано: АВС а АС Найти: L 1+L 2 +L 3 4 5 Ответ: L1+L2+L3= 180'. "Теорема о сумме углов треугольника.". 1 ...Геометрия
Həndəsİ fiqurlarIn qruplaşdIrIlmasI. TƏDQIQAT SUALI. BÜTÜN HƏNDƏSI FIQURLAR EYNI OLSA YDI NƏ OLARDI? . 1. Şəklə bax! Kvadratları göy, üçbucağı sarı, ...Геометрия
Содержание:. Координаты вектора Связь между координатами вектора и координатами его начала и конца Уравнения окружности и прямой Синус, Косинус, Тангенс ...Геометрия повторение
Назовите изображённые фигуры. отрезок луч прямая. Вспомните их определения. Какая фигура называется углом? Какой угол называется прямым, острым, тупым? ...Геометрия «Параллельность прямой и плоскости»
Параллельные прямые. Параллельные прямые – две прямые в пространстве, которые лежат в одной плоскости и не пересекаются. Параллельность прямых обозначается ...Геометрия четырехугольник
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказаны великим французским ...Геометрия «Параллельный перенос»
Упражнение 1. Докажите, что параллельный перенос является движением. Доказательство. Пусть параллельный перенос на вектор переводит точки A и B соответственно ...Повторение «Решение треугольников» Геометрия
Теорема синусов. Синусы углов треугольника пропорциональны противоположным сторонам. а в с С В А. Теорема косинусов. Для треугольника АВС справедливо ...Геометрия «Пирамида»
Бертран Рассел. Математика владеет не только истиной, но и высшей красотой-красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному ...Геометрия Евклида и геометрия Лобачевского. Сходства и отличия
Евклидова геометрия. Евкли́д или Эвкли́д (, ок. 300 г. до н. э.) — древнегреческий математик. Мировую известность приобрёл благодаря сочинению по ...Конспекты
Геометрия треугольника
Тема урока:. . «Геометрия треугольника». Тип урока: обобщающий урок по курсу геометрии. . Форма проведения урока: урок - бенефис». Цель урока:. ...Геометрия окружности
Урок математики в 9 классе. учителя МОУ «СОШ № 20» г. Энгельса. Милюткиной Людмилы Николаевны. и учителя математики МОУ «СОШ № 21» г. Энгельса. ...Геометрия вокруг нас…
Муниципальное бюджетное общеобразовательное учреждение. средняя общеобразовательная школа № 18. Кировский район городской округ город Уфа. . ...Геометрия вокруг нас
Разработала: Ильенко Анжела Владиславовна. Учитель начальных классов МБОУ СОШ №2 г. Стрежевого Томской области. Занятие для учеников 4х кл. по теме ...Геометрия в природе
Класс. : 8. Тема. «Геометрия в природе. ». Тип урока. : урок творческого развития. Цели:. Общеобразовательные:. 1. Систематизировать знаний ...Геометрия в ГИА
Сигайло Елена Валерьевна, учитель математики. МБОУ. . «Средняя общеобразовательная школа пос. Октябрьский». . пос. Октябрьский Лысогорского района ...Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно).
- Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно просто читать информацию со слайдов, ее аудитория может прочитать и сама.
- Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая информация, остальное лучше рассказать слушателям устно.
- Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации, а также правильно подобрать сочетание фона и текста.
- Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете первым, как закончите презентацию. Все приходит с опытом.
- Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его выступления.
- Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете меньше волноваться.
Информация о презентации
Дата добавления:7 сентября 2018
Категория:Математика
Классы:
Содержит:21 слайд(ов)
Поделись с друзьями:
Скачать презентацию