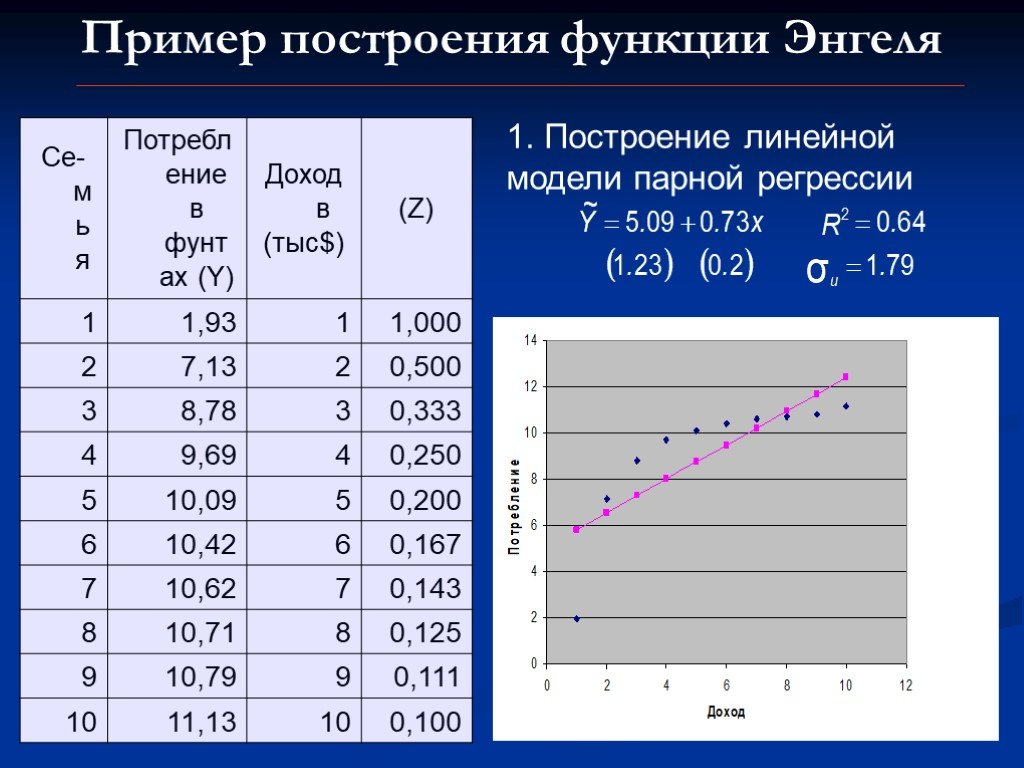
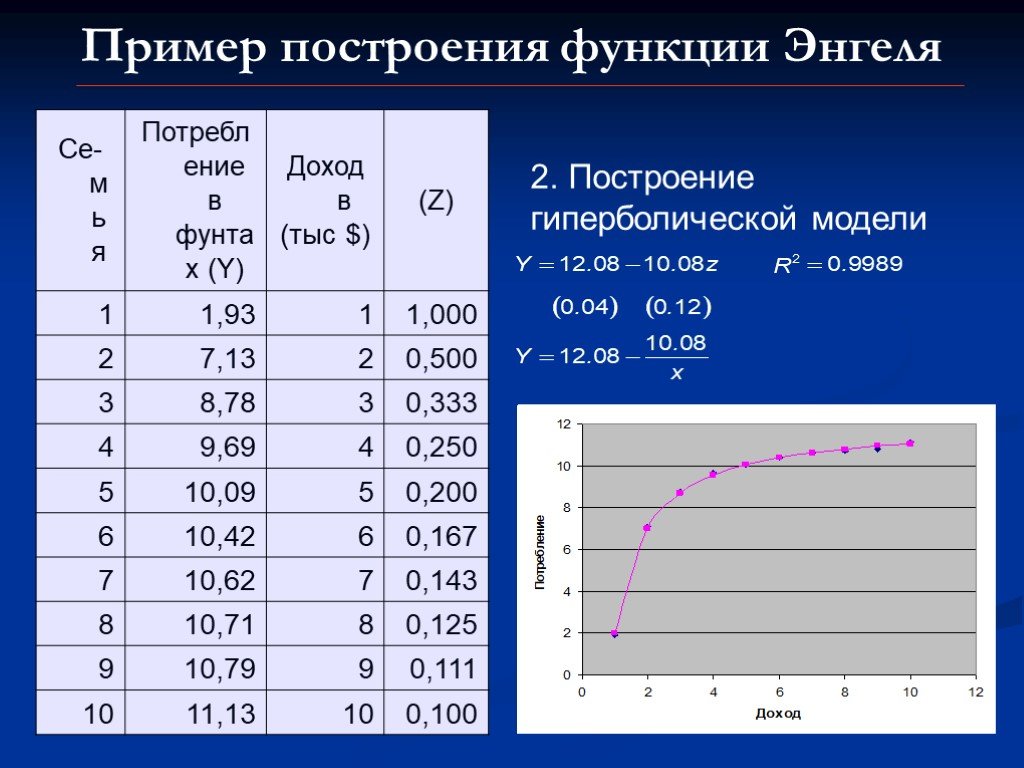
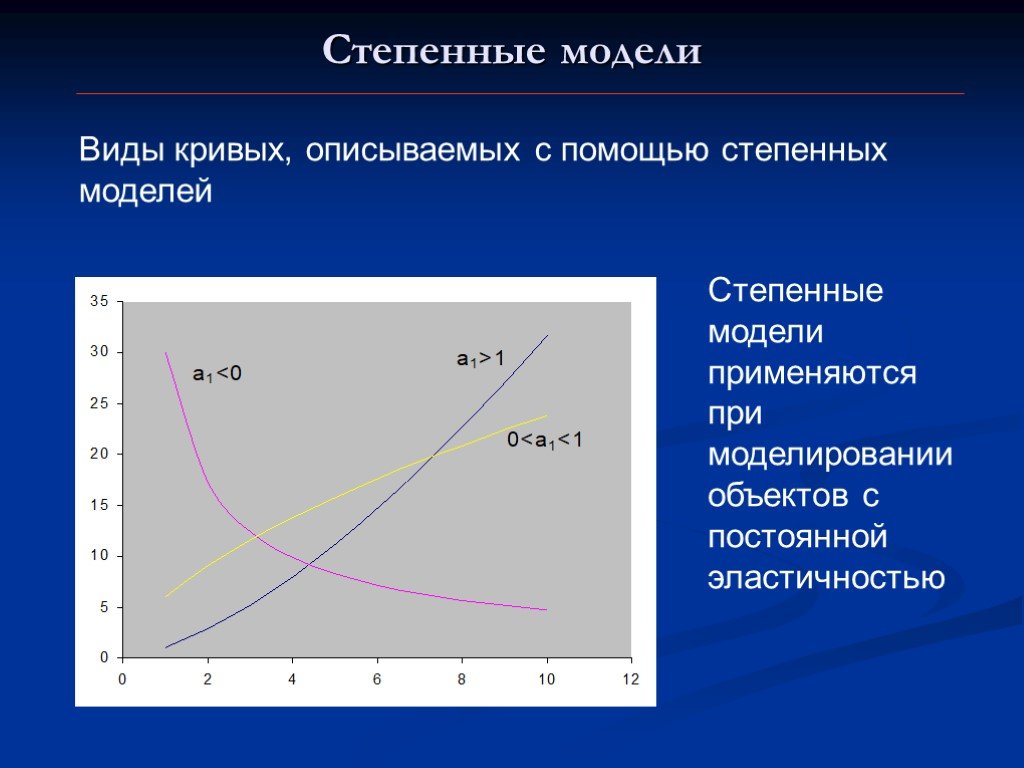
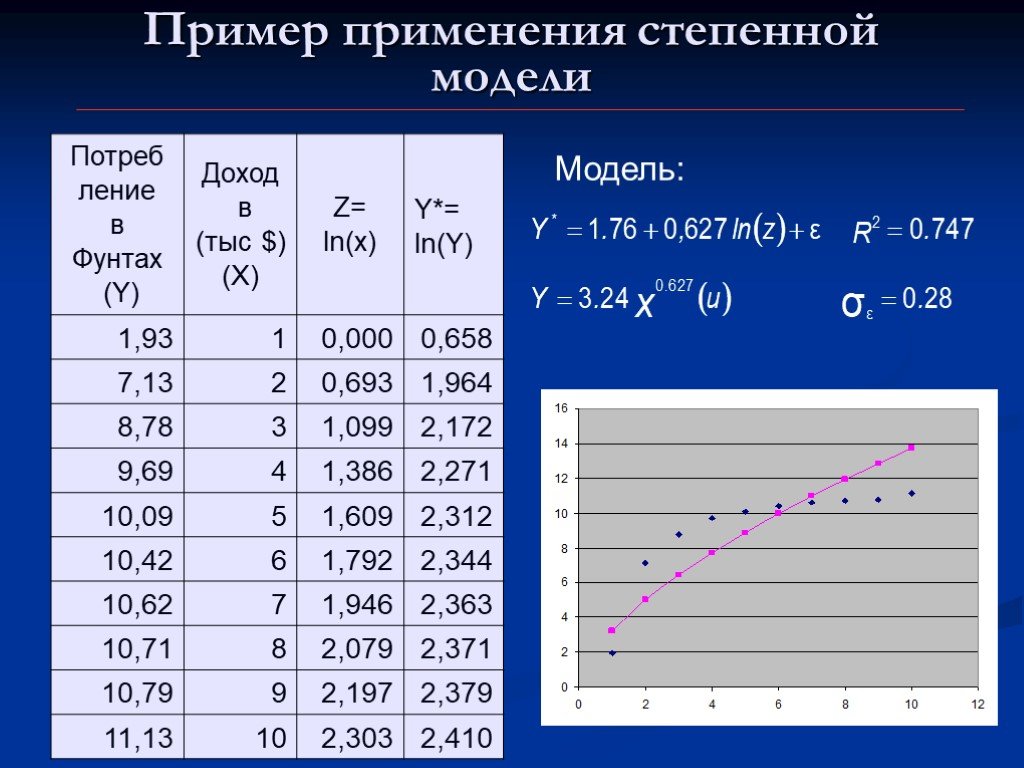
Презентация "Построение некоторых типов нелинейных моделей" по математике – проект, доклад

Построение некоторых типов нелинейных моделей

Нелинейные модели

Линейные модели двух типов: - линейные по переменным - линейные по параметрам Примеры. 1. Линейная модель множественной регрессии:

Является линейной как по переменным, так и по параметрам 2. Производственная функция Кобба-Дугласа:

Является нелинейной как по переменным, так и параметру а1

Основные типы нелинейных моделей

1.Обобщенная модель нелинейная по переменным

2. Степенные функции

3. Показательные функции

(1) (2)

Обобщенная модель нелинейная по переменным

Линеаризация обобщенной нелинейной модели 1. Вводятся новые переменные:

2. Подставляя новые переменные в модель (1), получим модель линейную по переменным z:

(1.1) (1.2)

3. После оценки параметров модели делается обратный переход к модели (1.1)

Примеры. 1. Полиномиальные модели:

Новые переменные:

После перехода к новым переменным получается линейная модель множественной регрессии:

Оценка и анализ проводится уже известными методами

(1.3)

Полиномиальные модели: Параболические модели широко применяются - при моделировании средних и предельных издержек в зависимости от объема выпуска продукции - при моделировании зависимости прибыли предприятия от расходов на рекламу Кубические модели – при моделировании общих издержек в зависимости от объема выпуска продукции

2. Модели гиперболического типа

Новая переменная:

В результате подстановки получим уравнение парной регрессии в виде:

(1.4)

Модели параболического вида нашли применение при моделировании: - зависимости спроса от цен - зависимости спроса от дохода (кривые Энгеля) - спрос на предметы роскоши от дохода (функции Торнквиста) - уровня относительного изменения заработной платы в зависимости от относительного изменения уровня безработицы (кривая Филлипса)

Пример построения функции Энгеля

1. Построение линейной модели парной регрессии

2. Построение гиперболической модели

Меняется экономический смысл параметров модели: Линейная модель а0 – минимально необходимое потребление, а1 – предельное потребление - Гиперболическая модель: а0 – максимальное потребление, а1 – экономической интерпретации не имеет

Предельное потребление равно: Эластичность:

Пример временного ряда

3. Временные ряды (динамические модели) Например вида:

где f(t) – функция временного тренда T – период внутри которого производится моделирование

Степенные модели

Степенная модель нелинейна по параметрам

1. Метод линеаризации – логарифмирование с последующим введением новых переменных:

2. Вводятся новые переменные и параметры:

В новых переменных исходное уравнение принимает вид уравнения множественной регрессии:

(2.1) (2.2) (2.3)

3. Оцениваются параметры b0, b1, b2 – методом наименьших квадратов и проверяются гипотезы о выполнении предпосылок теоремы Гаусса-Маркова для модели (2.3) 4. Осуществляется возврат к исходной модели (2.1):

В частном случае, когда в модели присутствует одна экзогенная переменная модель называют двойной логарифмической

Экономическая интерпретация параметров двойной логарифмической модели

Двойная логарифмическая модель:

(2.4)

Дифференцируем (2.4) по х

Откуда получаем, что:

Параметр а1 имеет смысл эластичности переменной Y по переменной x

Виды кривых, описываемых с помощью степенных моделей

Степенные модели применяются при моделировании объектов с постоянной эластичностью

Пример применения степенной модели

Модель:

Показательные функции в моделях

Показательная (экспоненциальная) Модель

(3.1)

1. Метод линеаризации - логарифмирование

2. Введение новых переменных и параметров:

3. Оценка линейной регрессионной модели

4. Обратный переход к исходной модели (3.1)

(3.2)

Экономическая интерпретация коэффициентов модели Дифференцируем уравнение (3.1) по Х

Экономический смысл коэффициента а1 в модели (3.1) – темп роста переменной Y Коэффициент а0 – начальное значение переменной Y Показательные функции находят применение при моделировании процессов с постоянным темпом роста

Полулогарифмические модели

Экспоненциальную модель (3.1) в виде (3.2) называют также полулогарифмической. К полуэкспоненциальным относят также модель вида:

С помощью моделей вида (3.3) описывают процессы, обладающие свойством насыщения. Например, кривые Энгеля для товаров повседневного спроса.

(3.3)

Кинематические функции Перла-Рида

Вид функции:

1. Способ линеаризации - логарифмирование

2. Вод новых переменных

3. Переход к модели множественной регрессии в новых переменных

(4.1) (4.2) (4.3)

Сложная экспоненциальная модель

Общий вид модели

Линеаризация в два этапв: 1. Логарфмирование

После введения переменной Y*=ln(Y), получится модель типа (1.1)

(5.1) (5.2)