Конспект урока «Система нелинейных неравенств с двумя переменными» по математике для 9 класса

Зарипова Гульфира Абдулгаязовна, учитель математики, КГУ «СОШ № 31», г. Семей, ВКО эл. адрес: zaripova-gulfira@mail.ru

Разработка урока 9 класс

Тема: Система нелинейных неравенств с двумя переменными

Цели и задачи урока:

• Ввести понятие системы нелинейных неравенств с двумя переменными.

• Составить алгоритм решения систем неравенств

• Формировать навыки решения систем неравенств

• Развивать «критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

• Воспитывать интерес к предмету, самостоятельность .

Ход урока:

1. Организационный момент.

Вступительное слово учителя.

На предыдущих уроках мы решали неравенства с двумя переменными. Сегодня мы переходим к изучению новой темы «Система нелинейных неравенств с двумя переменными». Но сначала повторим материал прошлого урока.

2. Устная работа учащихся с использованием интерактивной доски:

1) Какая из пар чисел (-2; 0), (0; 0), (1; 4) является решением неравенства х² + у² ≥ 4?

2) Найдите любое решение неравенства 2х – 5у ≤ - 3.

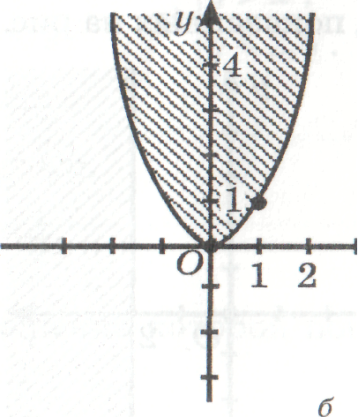
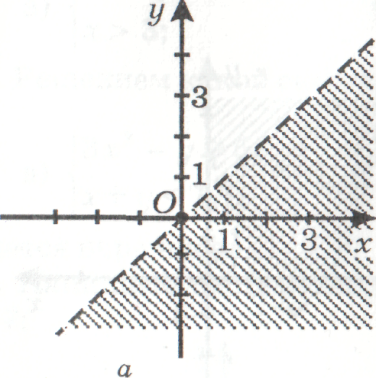
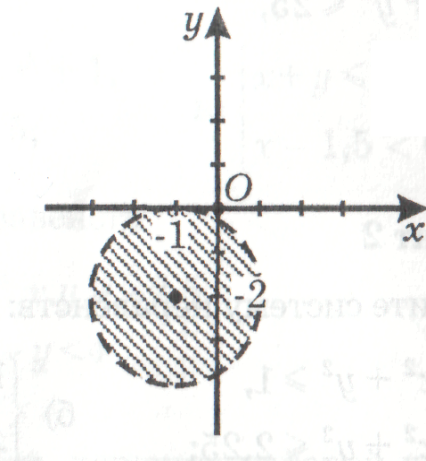
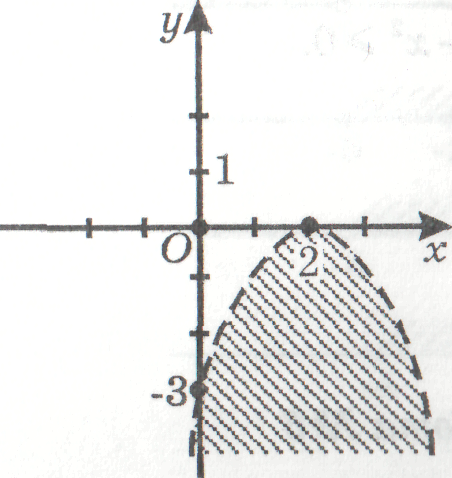
3) определите соответствие между заданными неравенствами и графиками, являющими

решениями данных неравенств:

у ˂ x, у ˃ х³, (x + 1)² + (у - 2)² ˃ 0, у ˂ (x - 2)², у ˃ х²

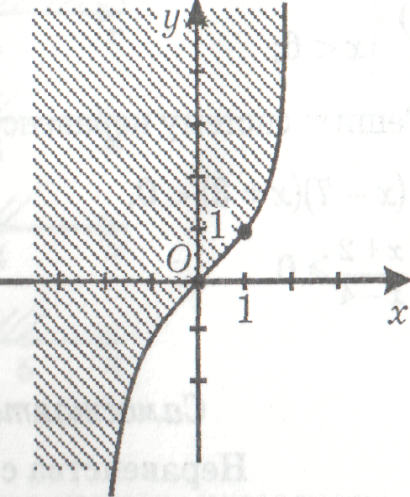
4) повторим алгоритм решения неравенства с двумя переменными:

а) определить вид функции, которая соответствует данному неравенству

б) построить график этой функции на координатной плоскости, т.е. разделить плоскость на две части

в) определить, какая часть плоскости является множеством решения данного неравенства, для чего необходимо взять любую точку на одной части плоскости и проверить выполняемость

3. Переходим к изучению новой темы: «Система нелинейных неравенств с двумя переменными».

Запишите в тетрадях число, тему урока.

Каковы цели сегодняшнего урока? Обсуждение с учениками.

Вывод : (цели урока) (слайд 5).

Итак, системой неравенств с двумя переменными является система вида: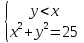

Каков же алгоритм решения систем неравенств? Выслушать учеников

Ученики самостоятельно предлагают алгоритм решения систем неравенств:

Если одно из неравенств системы представлено в виде у 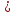f(x), то это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у 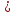f(x),то это неравенство задает на плоскости область, которая лежит не выше графика.

Если линия f(x;у)- замкнутая, например окружность, или замкнутая ломанная?

Учащиеся предлагают следующее правило:

Если f(x;у)=0- замкнутая линия, то неравенство f(x;у)>0, задает область лежащую вне замкнутой линии, а неравенство f(x;у)

И наиболее универсальное, полезное для проверки правило- «Правило пробной точки» .

Построить F(x;y) = 0 и G(x;y) = 0

Взяв из каждой области пробную точку, установить, являются ли ее координаты решением системы

Объединение полученных областей - решение системы неравенств. Решение неравенства с двумя переменными, а тем более системы неравенств с двумя переменными, представляется достаточно сложной задачей. Однако есть простой алгоритм, который помогает легко и без особых усилий решать на первый взгляд очень сложные задачи такого рода. Попробуем в нем разобраться.

Пусть мы имеем неравенство с двумя переменными одного из следующих видов:

y > f(x); y ≥ f(x); y

Для изображения множества решений такого неравенства на координатной плоскости поступают следующим образом:

1. Строим график функции y = f(x), который разбивает плоскость на две области.

2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают во множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.

А теперь рассмотрим несколько задач на эту тему.

Задача 1.

Какое множество точек задается неравенством x · y ≤ 4?

Решение.

1) Строим график уравнения x · y = 4. Для этого сначала преобразуем его. Очевидно, что x в данном случае не обращается в 0, так как иначе мы бы имели 0 · y = 4, что неверно. Значит, можем разделить наше уравнение на x. Получим: y = 4/x. Графиком данной функции является гипербола. Она разбивает всю плоскость на две области: ту, что между двумя ветвями гиперболы и ту, что снаружи их.

2) Выберем из первой области произвольную точку, пусть это будет точка (4; 2).

Проверяем неравенство: 4 · 2 ≤ 4 – неверно.

Значит, точки данной области не удовлетворяют исходному неравенству. Тогда можем сделать вывод о том, что множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.

3) Так как неравенство нестрогое, то граничные точки, то есть точки графика функции y = 4/x, рисуем сплошной линией.

Закрасим множество точек, которое задает исходное неравенство, желтым цветом (рис. 1).

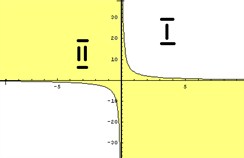
Задача 2.

Изобразить область, заданную на координатной плоскости системой

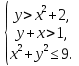
Решение.

Строим для начала графики следующих функций (рис. 2):

y = x² + 2 – парабола,

y + x = 1 – прямая

x² + y² = 9 – окружность.

Теперь разбираемся с каждым неравенством в отдельности.

1. y > x² + 2.

2. Берем точку (0; 5), которая лежит выше графика функции.

Проверяем неравенство: 5 > 0 ∙ 2 + 2 – верно.

Следовательно, все точки, лежащие выше данной параболы y = x² + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.

2) y + x > 1.

Берем точку (0; 3), которая лежит выше графика функции.

Проверяем неравенство: 3 + 0 > 1 – верно.

Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют второму неравенству системы. Закрасим их зеленой штриховкой.

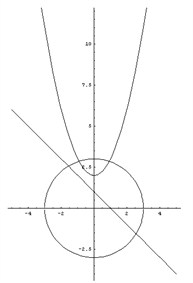
3) x² + y² ≤ 9.

Берем точку (0; -4), которая лежит вне окружности x² + y² = 9.

Проверяем неравенство: 0∙2 + (-4) ∙ 2 ≤ 9 – неверно.

Следовательно, все точки, лежащие вне окружности x² + y² = 9, не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x² + y² = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.

Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром. Получаем следующую картинку (рис. 3).

Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис. 4).

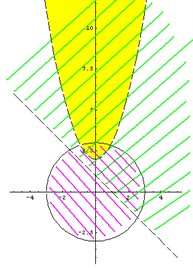
Рис 3

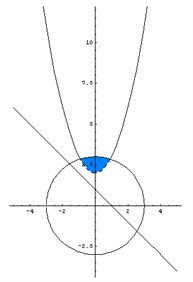рис 4

Задача 3.

Изобразить область, заданную на координатной плоскости системой:

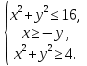
Решение.

Строим для начала графики следующих функций:

X² + y² = 16 – окружность,

x = -y – прямую,

x² + y² = 4 – окружность (рис. 5).

Теперь разбираемся с каждым неравенством в отдельности.

1) x² + y² ≤ 16.

Берем точку (0; 0), которая лежит внутри окружности x² + y² = 16.

Проверяем неравенство: 0 ∙ 2 + 0 ∙ 2 ≤ 16 – верно.

Следовательно, все точки, лежащие внутри окружности x² + y² = 16, удовлетворяют первому неравенству системы.

Закрасим их красной штриховкой.

2) x ≥ -y.

Берем точку (1; 1), которая лежит выше графика функции.

Проверяем неравенство: 1 ≥ -1 – верно. Следовательно, все точки, лежащие выше прямой x = -y, удовлетворяют второму неравенству системы. Закрасим их синей штриховкой.

3) x² + y² ≥ 4.

Берем точку (0; 5), которая лежит вне окружности x² + y² = 4.

Проверяем неравенство: 0 ∙ 2 + 5 ∙ 2 ≥ 4 – верно.

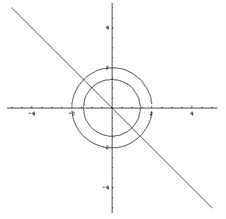рис 5

Следовательно, все точки, лежащие вне окружности x² + y² = 4, удовлетворяют третьему неравенству системы. Закрасим их голубым цветом.

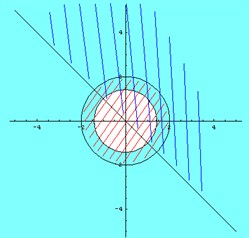рис 6

В данной задаче все неравенства нестрогие, значит, все границы рисуем сплошной линией. Получаем следующую картинку (рис. 6).

Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис 7).

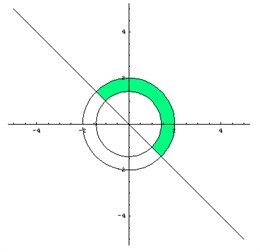
Рис 7

4. Решение задач:

№ 117 учебника

5. Домашнее задание:

6. Итог:

1). Чем отличаются способы решения системы уравнений и системы неравенств?

2). Что является решением системы нелинейных неравенств с двумя переменными?

3). Как правильно указать множество решений неравенства на координатной плоскости?