Конспект урока «Решение линейных неравенств» по математике для 8 класса
Земляникина Елена Александровна
учитель математики
МБОУ СОШ № 1 г. Лакинска
Владимирской области
Тема: Решение линейных неравенств
Класс: 8
Тип урока: урок изучения нового материала
Цель: начать формирование навыков решения линейных неравенств
1 этап. Мотивационный.
Учитель обращается к классу: «Серьезность изучаемых в школе предметов не мешает нам творчески переосмысливать новые знания. Думая о сегодняшнем уроке, я почти случайно зарифмовала свои размышления. Послушайте, что у меня получилось, и попробуйте определить тему урока».
В математике - соотношенье между числами и выраженьями,
В них и знаки для сравнения: меньше, больше иль равно?
Я вам дам одну подсказку, вполне полезную возможно,
Мир объединяет равенство, частица «не» указывает на ……
(неравенство)
Итак, тема урока «Неравенства».
2 этап. Изучение нового материала.
Стадия осмысления: (5 мин) (добывание учащимися знаний)
(применяю прием маркировки текста «Инсерт» - учащиеся читают текст, вникают в него, делают специальные пометки)
Отмечают «+» то, что им уже известно, «-» то, что новое, не знакомо.
Текст
Неравенство – это два числа или выражения, соединенные одним из знаков: > (больше),
Линейное неравенство – это неравенство вида ax + b > 0 (или ax + b , где а и b – любые числа, причем а ≠ 0.
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Например, х + 5 Подставив вместо х значение 1, получим 1+ 5 верное числовое неравенство. Значит, х = 1 –решение данного неравенства.
Решить неравенство – это значит найти все его решения или доказать, что решений нет.
Свойства числовых неравенств:
-
Если а > b и b > c, то а > с.
-
Если а > b, то а + с > b + с.
-
Если а > b и m > 0, то аm > bm;
Если а > b и m am bm.
-
Если а > b и с > d, то a + c > b + d.
-
Если а > b и с > d, то ac > bd, где а, b, c, d – положительные числа.
-
Если а > b, а и b – неотрицательные числа, то aⁿ > bⁿ , n – любое натуральное число.
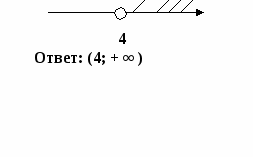
| Пример: Решить неравенство: 5∙(х – 3) > 2х -3 | |
4. Разделить обе части неравенства на число, стоящее перед х (если это число положительное, то знак неравенства не меняется; если это число отрицательное, то знак неравенства меняется на противоположный): 5Перейти от аналитической модели х > 4 к геометрической модели:
| 5х – 15 > 2х -3 5х – 2х > -3 + 15 3х > 12 3х > 12 / (:3) х > 4 Х 4 Ответ: (4; + ∞ ) |
Фаза рефлексии: (беседа с классом по вопросам)
Учитель составляет «Кластер» на доске.
-
Что из того, что вы прочитали, вам уже было знакомо?
-
Что из того, что вы прочитали, оказалось новой информацией?
-
А что вам напоминает алгоритм решения линейного неравенства?
Линейные
Свойства числовых неравенств: Если а > b и b > c, то а > с. Если а > b, то а + с > b + с. Если а > b и m > 0, то аm > bm; Если а > b и m am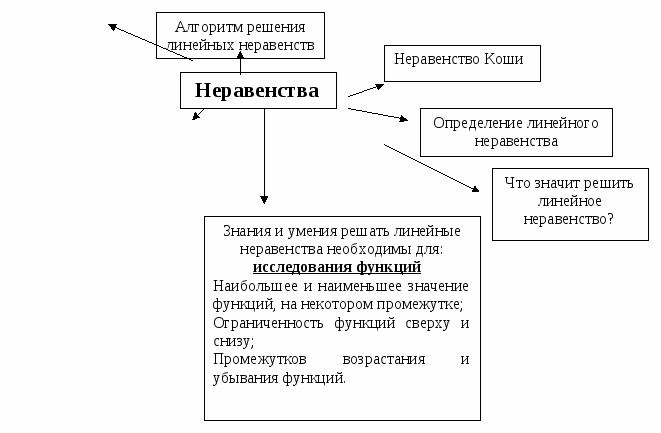
-
Если а > b и с > d, то a + c > b + d.
-
Если а > b и с > d, то ac > bd,
а, b, c, d – положительные числа.
6. Если а > b, а и b – неотриц. числа, то aⁿ > bⁿ.
Определение неравенства
>,
(строгое и нестрогое)
Судя по этой схеме, вы уже многое знаете о неравенствах, а сегодня на уроке мы расширим эти знания.
3 этап. Закрепление нового материала.
(отработка навыков решения линейных неравенств)
Стратегия «Зигзаг»: (в группе по 5 человек, 5 групп) (отработка навыков решения линейных уравнений: каждый ученик получает свое неравенство, решает, применяя алгоритм решения линейного неравенства, затем обсуждение в группах и объяснение другим ученикам).
1. Попытка решить самому!!! 5 мин
Задание: Решить неравенство и изобразить множество его решений на координатной прямой.
№ 1 17 – х > 2∙(5 – 3х)
№ 2 2∙(32 – 3х) ≥ 1- х
№ 3 8 + 5х ≤ 3∙(7 + 2х)
№ 4 2∙(0,1х – 1)
№ 5 5х + 2 ≤ 1 – 3∙(х + 2)
2. Разбор задания в группе. 5 мин
Переходят в экспертные группы с одинаковым заданием. Обсуждают решения, консультируют друг друга и исправляют свои ошибки, если они есть. Необходимо, чтобы каждый понял решение своего неравенства.
Учитель выступает в роли консультанта.
(Ученик сам – группа учеников --- учитель)
3. Взаимообучение. 5-7 мин Ученики возвращаются на свои места и рассказывают ход решения своего неравенства по очереди другим, идет запись в тетрадь неравенств.
Задача группы: чтобы каждый овладел алгоритмом решения линейных неравенств.
После того, как ученики готовы идет самопроверка нескольких уравнений через ИКТ, нескольких у доски.
Обсуждение (беседа): Кто верно выполнил решение всех неравенств («один за всех и все за одного») поднимите руку? Кто допустил ошибки? Где и почему?
Если позволит время: для тех, кто не ошибся решить (или в качестве домашнего задания) творческое задание (одно на выбор) и сделать к нему соответствующий вывод:
1) 2(х + 8) – 5х
2) х + 2х – 1 > 2х – 1
3 5 15
3) При каких значениях х двучлен 5х – 7 принимает положительные значения?
4 этап. Подведение итогов.
Ребята! Чем мы на уроке занимались? Чему учились?
Давайте вспомним: Что значит решить неравенство? Чем мы будем пользоваться при решении неравенства? (обратить еще раз внимание на алгоритм)
Ребята! Как вы думаете, кто сегодня отличился на уроке? (оценивают себя сами)
5этап. Домашнее задание. П.34 В программе (для создания слайдов) выполнить презентацию о неравенстве Коши.
Хочу я вам дать совет:
«Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий»
А.И. Маркушевич
Текст
Неравенство – это два числа или выражения, соединенные одним из знаков: > (больше),
Линейное неравенство – это неравенство вида ax + b > 0 (или ax + b ,
где а и b – любые числа, причем а ≠ 0.
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Например, х + 5 Подставив вместо х значение 1, получим 1+ 5 верное числовое неравенство.
Значит, х = 1 – решение данного неравенства.
Решить неравенство – это значит найти все его решения или доказать, что решений нет.
Свойства числовых неравенств:
-
Если а > b и b > c, то а > с.
-
Если а > b, то а + с > b + с.
-
Если а > b и m > 0, то аm > bm;
Если а > b и m am bm.
-
Если а > b и с > d, то a + c > b + d.
-
Если а > b и с > d, то ac > bd,
а, b, c, d – положительные числа.
6. Если а > b, а и b – неотрицательные числа, то aⁿ > bⁿ , n – любое натуральное число.
| Пример: Решить неравенство: 5∙(х – 3) > 2х -3 | |
2. Перенести все слагаемые с х влево, а числа вправо, меняя при этом знак: 3. Привести подобные слагаемые: 4. Разделить обе части неравенства на число, стоящее перед х (если это число положительное, то знак неравенства не меняется; если это число отрицательное, то знак неравенства меняется на противоположный): 5. Перейти от аналитической модели х > 4 к геометрической модели: 6. Указать множество решений данного неравенства, записав ответ: | 5х – 15 > 2х -3 5х – 2х > -3 + 15 3х > 12
3·х > 12 / (:3)
х > 4 Х
|
Здесь представлен конспект к уроку на тему «Решение линейных неравенств», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (8 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.